Multiphysics for an SFR Pincell

In this tutorial, you will learn how to:

  • Couple OpenMC, NekRS, and MOOSE for modeling an Sodium Fast Reactor (SFR) pincell

  • Use MOOSE's reactor module to make meshes for common reactor geometries

  • Use subcycling to efficiently allocate computational resources

To access this tutorial,

cd cardinal/tutorials/pincell_multiphysics

Geometry and Computational Model

The geometry consists of a single pincell, cooled by sodium. The dimensions and assumed operating conditions are summarized in Table 1. Note that these conditions are not necessarily representative of full-power nuclear reactor conditions, since we elect laminar flow conditions in order to reduce meshing requirements for the sake of a fast-running tutorial. By using laminar flow, we will also use a much lower power density than seen in prototypical systems - but for the sake of a tutorial, all the essential components of multiphysics are present (coupling via power, temperature, and density). In addition, to keep the computational requirements as low as possible for NekRS, the height is only 50 cm (so the eignevalue predicted by OpenMC will also be very low, due to high axial leakage).

Table 1: Geometric and operating specifications for a pincell

ParameterValue
Fuel pellet diameter, dfd_f0.825 cm
Clad outer diameter, dcd_c0.97 cm
Pin pitch, pp1.28 cm
Height50.0 cm
Reynolds number500.0
Prandtl number0.00436
Inlet temperature573 K
Outlet temperature708 K
Power250 W

We will couple OpenMC, NekRS, and MOOSE heat conduction in a "single stack" hierarchy, with OpenMC as the main application, MOOSE as the second-level application, and NekRS as the third-level application. This structure is shown in Figure 1, and will allow us to sub-cycle all three codes with respect to one another. Solid black lines indicate data transfers that occur directly from application AA to application BB, while the dashed black lines indicate data transfers that first have to pass through an "intermediate" application.

Figure 1: "Single stack" multiapp hierarchy used in this tutorial.

Like with all Cardinal simulations, Picard iterations are achieved "in time." We have not expounded greatly upon this notion in previous tutorials, so we dedicate some space here. The overall Cardinal simulation has a notion of "time" and a time step index, because all code applications will use a Transient executioner. However, usually only NekRS is solved with non-zero time derivatives. The notion of time-stepping is then used to customize how frequently (i.e., in units of time steps) data is exchanged. To help explain the strategy, represent the time step sizes in NekRS, MOOSE, and OpenMC as Δtnek\Delta t_{nek}, Δtbison=MΔtnek\Delta t_{bison}=M\Delta t_{nek}, and Δtopenmc=NMΔtnek\Delta t_{openmc}=NM\Delta t_{nek}, respectively. Selecting N≠1N\neq1 and/or M≠1M\neq1 is referred to as "sub-cycling." In other words, NekRS runs MM times for each MOOSE solve, while MOOSE runs NN times for each OpenMC solve, effectively reducing the total number of MOOSE solves by a factor of MM and the total number of OpenMC solves by a factor of NMNM compared to the naive approach to exchange data based on the smallest time step across the coupled codes. We can then also reduce the total number of data transfers by only transferring data when needed. Each Picard iteration consists of:

  • Run an OpenMC kk-eigenvalue calculation. Transfer the heat source q˙s\dot{q}_s to MOOSE.

  • Repeat NN times:

    • Run a steady-state MOOSE calculation. Transfer the heat flux q′′q^{''} to NekRS.

    • Run a transient NekRS calculation for MM time steps. Transfer the wall temperature TwallT_\text{wall} to MOOSE.

  • Transfer the solid temperature TsT_s, the fluid temperature TfT_f, and the fluid density ρf\rho_f to OpenMC.

Figure 2 shows the procedure for an example selection of N=3N=3, meaning that the MOOSE-NekRS sub-solve occurs three times for every OpenMC solve.

Figure 2: Coupling procedure with subcycling for a calculation with OpenMC, MOOSE, and NekRS

In this tutorial, we will use different "time steps" for OpenMC, MOOSE, and NekRS, and we invite you at the end of the tutorial to explore the impact on changing these time step magnitudes to see how you can control the frequency of data transfers.

OpenMC Model

OpenMC is used to solve for the neutron transport and power distribution. The OpenMC model is created using OpenMC's Python API. We will build this geometry using CSG and divided the pincell into a number of axial layers. On each layer, we will apply temperature and density feedback from the coupled MOOSE-NekRS simulation.

First, we create a number of materials to represent the fuel pellet and cladding. Because these materials will only receive temperature updates (i.e. we will not change their density, because doing so would require us to move cell boundaries in order to preserve mass), we can simply create one material that we will use on all axial layers. Next, we create a number of materials to represent the sodium material in each axial layer of the model. Because the sodium cells will change both their temperature and density, we need to create a unique material for each axial layer.

Next, we divide the geometry into a number of axial layers, where on each layer we set up cells to represent the pellet, cladding, and sodium. Each layer is then described by lying between two zz-planes. The boundary condition on the top and bottom faces of the OpenMC model are set to vacuum. Finally, we declare a number of settings related to the initial fission source (uniform over the fissionale regions) and how temperature feedback is applied, and then export all files to XML.

from argparse import ArgumentParser
import numpy as np
import openmc

R = 0.97 / 2.0           # outer radius of the pincell (cm)
Rf = 0.825 / 2.0         # outer radius of the pellet (cm)
pitch = 1.28             # pitch between pincells (cm)
height = 50.0            # height of the pincell (cm)
T_inlet = 573.0          # inlet sodium temperature (K)

ap = ArgumentParser()
ap.add_argument('-n', dest='n_axial', type=int, default=25,
                help='Number of axial cell divisions')

args = ap.parse_args()
N = args.n_axial

all_materials = []

# Then, add the materials for UO2 and zircaloy
uo2 = openmc.Material(name = 'UO2')
uo2.set_density('g/cm3', 10.29769)
uo2.add_element('U', 1.0, enrichment = 2.5)
uo2.add_element('O', 2.0)
all_materials.append(uo2)

zircaloy = openmc.Material(material_id=3, name='Zircaloy 4')
zircaloy.set_density('g/cm3', 6.55)
zircaloy.add_element('Sn', 0.014, 'wo')
zircaloy.add_element('Fe', 0.00165, 'wo')
zircaloy.add_element('Cr', 0.001, 'wo')
zircaloy.add_element('Zr', 0.98335, 'wo')
all_materials.append(zircaloy)

sodium_materials = []

for i in range(N):
  sodium = openmc.Material(name = 'sodium{:n}'.format(i))
  sodium.set_density('g/cm3', 1.0)
  sodium.add_element('Na', 1.0)

  sodium_materials.append(sodium)
  all_materials.append(sodium)

materials = openmc.Materials(all_materials)
materials.export_to_xml()

pincell_surface = openmc.ZCylinder(r = R, name = 'Pincell outer radius')
pellet_surface = openmc.ZCylinder(r = Rf, name = 'Pellet outer radius')
rectangular_prism = openmc.model.RectangularPrism(width = pitch, height = pitch, axis = 'z', origin = (0.0, 0.0), boundary_type = 'reflective')

axial_coords = np.linspace(0.0, height, N + 1)
plane_surfaces = [openmc.ZPlane(z0=coord) for coord in axial_coords]
plane_surfaces[0].boundary_type = 'vacuum'
plane_surfaces[-1].boundary_type = 'vacuum'

fuel_cells = []
clad_cells = []
sodium_cells = []

for i in range(N):
  # these are the two planes that bound the current layer on top and bottom
  layer = +plane_surfaces[i] & -plane_surfaces[i + 1]

  fuel_cells.append(openmc.Cell(fill = uo2, region = -pellet_surface & layer, name = 'Fuel{:n}'.format(i)))
  clad_cells.append(openmc.Cell(fill = zircaloy, region = +pellet_surface & -pincell_surface & layer, name = 'Clad{:n}'.format(i)))

  # we need to get the correct sodium material that belongs to this layer
  sodium_material = sodium_materials[i]
  sodium_cells.append(openmc.Cell(fill = sodium_material, region = +pincell_surface & layer & -rectangular_prism, name = 'sodium{:n}'.format(i)))

root = openmc.Universe(name = 'root')
root.add_cells(fuel_cells)
root.add_cells(clad_cells)
root.add_cells(sodium_cells)

geometry = openmc.Geometry(root)
geometry.export_to_xml()

settings = openmc.Settings()

# Create an initial uniform spatial source distribution over fissionable zones
lower_left = (-pitch, -pitch, 0.0)
upper_right = (pitch, pitch, height)
uniform_dist = openmc.stats.Box(lower_left, upper_right, only_fissionable = True)

settings.source = openmc.IndependentSource(space=uniform_dist)

settings.batches = 50
settings.inactive = 10
settings.particles = 10000

settings.temperature = {'default': T_inlet,
                        'method': 'interpolation',
                        'multipole': True,
                        'range': (294.0, 3000.0)}

settings.export_to_xml()
(tutorials/pincell_multiphysics/pincell.py)

You can create these XML files by running

python pincell.py

Heat Conduction Model

The MOOSE heat transfer module is used to solve for energy conservation in the solid. The solid mesh is shown in Figure 3. This mesh is generated using MOOSE's reactor module, which can be used to make sophisticated meshes of typical reactor geometries such as pin lattices, ducts, and reactor vessels. In this example, we use this module to set up just a single pincell.

Figure 3: Solid mesh

This mesh is described in the solid.i file,

[Mesh]
  [pin]
    type = PolygonConcentricCircleMeshGenerator
    num_sides = 8
    num_sectors_per_side = '8 8 8 8 8 8 8 8'
    ring_radii = '${fparse 0.75 * Rf} ${fparse 0.85 * Rf} ${fparse 0.95 * Rf} ${Rf} ${R}'
    ring_intervals = '1 1 1 1 2'
    ring_block_ids = '2 2 2 2 3'
    polygon_size = '${fparse pin_pitch / 2.0}'
    background_block_ids = '1'
    quad_center_elements = true
  []
  [delete_background]
    type = BlockDeletionGenerator
    input = pin
    block = '1'
  []
  [fluid]
    type = PolygonConcentricCircleMeshGenerator
    num_sides = 4
    num_sectors_per_side = '10 10 10 10'
    ring_radii = '${R}'
    ring_intervals = '1'
    ring_block_ids = '500'
    polygon_size = '${fparse pin_pitch / 2.0}'
    background_block_ids = '1'
    background_intervals = 3
  []
  [delete_pin]
    type = BlockDeletionGenerator
    input = fluid
    block = '500'
  []
  [combine]
    type = CombinerGenerator
    inputs = 'delete_background delete_pin'
  []
  [extrude]
    type = AdvancedExtruderGenerator
    input = combine
    heights = ${height}
    num_layers = ${num_layers}
    direction = '0 0 1'
  []
  [rotate]
    type = TransformGenerator
    input = extrude
    transform = ROTATE
    vector_value = '45.0 0.0 0.0'
  []

  # We want boundary 5 to be the clad surface, because at the time we made this tutorial
  # that is what the reactor module named this boundary (so we drew that boundary in
  # some figures). If you are making a mesh from scratch, you dont need to go through
  # these gynmastics.
  [delete_5]
    type = BoundaryDeletionGenerator
    input = rotate
    boundary_names = '5'
  []
  [name_5]
    type = RenameBoundaryGenerator
    input = delete_5
    old_boundary = '9'
    new_boundary = '5'
  []
[]
(tutorials/pincell_multiphysics/solid.i)

You can generate this mesh by running

cardinal-opt -i solid.i --mesh-only

which will generate the mesh as the solid_in.e file. You will note in Figure 3 that this mesh actually also includes mesh for the fluid region. In Figure 1, we need a mesh region to "receive" the fluid temperature and density from NekRS, because NekRS cannot directly communicate with OpenMC by skipping the second-level app (MOOSE). Therefore, no solve will occur on this fluid mesh, it simply exists to receive the fluid solution from NekRS before being passed "upwards" to OpenMC. By having this dummy "receiving-only" mesh in the solid application, we will require a few extra steps when we set up the MOOSE heat conduction model in Solid Input Files .

NekRS Model

NekRS is used to solve the incompressible Navier-Stokes equations in non-dimensional form. The NekRS input files needed to solve the incompressible Navier-Stokes equations are:

  • fluid.re2: NekRS mesh (generated by exo2nek starting from MOOSE-generated meshes, to be discussed shortly)

  • fluid.par: High-level settings for the solver, boundary condition mappings to sidesets, and the equations to solve

  • fluid.udf: User-defined C++ functions for on-line postprocessing and model setup

  • fluid.oudf: User-defined OCCA kernels for boundary conditions and source terms

A detailed description of all of the available parameters, settings, and use cases for these input files is available on the NekRS documentation website. Because the purpose of this analysis is to demonstrate Cardinal's capabilities, only the aspects of NekRS required to understand the present case will be covered.

We first create the mesh using MOOSE's reactor module. The syntax used to build a HEX27 fluid mesh is shown below. A major difference from the dummy fluid receiving portion of the solid mesh is that we now set up some boundary layers on the pincell surfaces, by providing ring_radii (and other parameters) as vectors.

[Mesh]
  [pin]
    type = PolygonConcentricCircleMeshGenerator
    num_sides = 4
    polygon_size = '${fparse pin_pitch / 2.0}'
    num_sectors_per_side = '6 6 6 6'
    uniform_mesh_on_sides = true

    ring_radii = '${fparse pin_diameter / 2.0} ${bl_0} ${bl_1} ${bl_2} ${bl_3} ${bl_4} ${bl_5}'
    ring_intervals = '1 1 1 1 1 1 1'
    ring_block_ids = '${fparse fluid_id + 1} ${fluid_id} ${fluid_id} ${fluid_id} ${fluid_id} ${fluid_id} ${fluid_id}'

    background_block_ids = '${fparse fluid_id}'
    background_intervals = 6
  []
  [pin_surface]
    type = SideSetsBetweenSubdomainsGenerator
    input = pin
    primary_block = ${fluid_id}
    paired_block = '${fparse fluid_id + 1}'
    new_boundary = '1'
  []
  [delete_solid]
    type = BlockDeletionGenerator
    input = pin_surface
    block = '${fparse fluid_id + 1}'
  []
  [rotate]
    type = TransformGenerator
    input = delete_solid
    transform = rotate
    vector_value = '45.0 0.0 0.0'
  []

  # We will name boundaries in the mesh for sidesets 2 - 7 using other MOOSE objects.
  # The reactor module does its own sideset naming, so we make sure those IDs are
  # free by deleting whatever the reactor module had.
  [delete_extra_surfaces]
    type = BoundaryDeletionGenerator
    input = rotate
    boundary_names = '2 3 4 5 6 7'
  []
  [extrude]
    type = AdvancedExtruderGenerator
    input = delete_extra_surfaces
    direction = '0 0 1'
    num_layers = '${num_layers}'
    heights = '${height}'
    bottom_boundary = '2'
    top_boundary = '3'
  []
  [lateral_boundaries]
    type = SideSetsFromNormalsGenerator
    input = extrude
    new_boundary = '4 5 6 7'
    normals = '1.0  0.0 0.0
              -1.0  0.0 0.0
               0.0  1.0 0.0
               0.0 -1.0 0.0'
    normal_tol = 1e-6
  []

  second_order = true
[]
(tutorials/pincell_multiphysics/fluid.i)

However, NekRS requires a HEX20 mesh format. Therefore, we use a NekMeshGenerator to convert from HEX27 to HEX20 format, while also moving the higher-order side nodes on the pincell surface to match the curvilinear elements. The syntax used to convert from the HEX27 fluid mesh to a HEX20 fluid mesh, while preserving the pincell surface, is shown below.

pin_diameter = 0.97e-2     # pin outer diameter
pin_pitch = 1.28e-2        # pin pitch

flow_area = ${fparse pin_pitch * pin_pitch - pi * pin_diameter * pin_diameter / 4.0}
wetted_perimeter = ${fparse pi * pin_diameter}
hydraulic_diameter = ${fparse 4.0 * flow_area / wetted_perimeter}

[Mesh]
  [file]
    type = FileMeshGenerator
    file = fluid_in.e
  []
  [to_hex20]
    type = NekMeshGenerator
    input = file
    boundary = '1'
    radius = ${fparse pin_diameter / 2.0}
    boundaries_to_rebuild = '1 2 3 4 5 6 7'
    layers = '4'
    geometry_type = cylinder
  []
  [scale]
    type = TransformGenerator
    input = to_hex20
    transform = scale
    vector_value = '${fparse 1.0 / hydraulic_diameter} ${fparse 1.0 / hydraulic_diameter} ${fparse 1.0 / hydraulic_diameter}'
  []
[]
(tutorials/pincell_multiphysics/convert.i)

To generate the meshes, we run:

cardinal-opt -i fluid.i --mesh-only
cardinal-opt -i convert.i --mesh-only
mv convert_in.e convert.exo

and then use the exo2nek utility to convert from the exodus file format (convert.exo) into the custom .re2 format required for NekRS. A depiction of the outputs of the two stages of the mesh generator process are shown in Figure 4. Boundary 2 is the inlet, boundary 3 is the outlet, and boundary 1 is the pincell surface. Boundaries 4 through 7 are the lateral faces of the pincell.

Figure 4: Outputs of the mesh generators used for the NekRS flow domain

Next, the .par file contains problem setup information. This input solves for pressure, velocity, and temperature. In the nondimensional formulation, the "viscosity" becomes 1/Re1/Re, where ReRe is the Reynolds number, while the "thermal conductivity" becomes 1/Pe1/Pe, where PePe is the Peclet number. These nondimensional numbers are used to set various diffusion coefficients in the governing equations with syntax like -500.0, which is equivalent in NekRS syntax to 1500.0\frac{1}{500.0}. On the four lateral faces of the pincell, we set symmetry conditions for velocity.

# Model of single SFR pincell, in non-dimensional form
#
# Pr = 0.00439
# Re = 500.0
# Pe = Re * Pr

[OCCA]
  backend = CPU

[GENERAL]
  stopAt = numSteps
  numSteps = 2000
  dt = 2.5e-3
  timeStepper = tombo2
  writeControl = steps
  writeInterval = 200
  polynomialOrder = 5

[VELOCITY]
  viscosity = -500.0
  density = 1.0
  boundaryTypeMap = w, v, O, symx, symx, symy, symy
  residualTol = 1.0e-7

[PRESSURE]
  residualTol = 1.0e-6

[TEMPERATURE]
  conductivity = -2.195
  rhoCp = 1.0
  boundaryTypeMap = f, t, I, I, I, I, I
  residualTol = 1.0e-6
(tutorials/pincell_multiphysics/fluid.par)

Next, the .udf file is used to set up initial conditions for velocity, pressure, and temperature. We set uniform axial velocity initial conditions, and temperature to a linear variation from 0 at the inlet to 1 at the outlet.

#include "udf.hpp"

#define LENGTH 42.35158086795113

void UDF_LoadKernels(occa::properties & kernelInfo)
{
}

void UDF_Setup(nrs_t *nrs)
{
  auto mesh = nrs->cds->mesh[0];

  // loop over all the GLL points and assign directly to the solution arrays by
  // indexing according to the field offset necessary to hold the data for each
  // solution component
  int n_gll_points = mesh->Np * mesh->Nelements;
  for (int n = 0; n < n_gll_points; ++n)
  {
    nrs->U[n + 0 * nrs->fieldOffset] = 0.0; // x-velocity
    nrs->U[n + 1 * nrs->fieldOffset] = 0.0; // y-velocity
    nrs->U[n + 2 * nrs->fieldOffset] = 1.0; // z-velocity

    nrs->P[n] = 0.0; // pressure

    nrs->cds->S[n + 0 * nrs->cds->fieldOffset[0]] = mesh->z[n] / LENGTH; // temperature
  }
}
(tutorials/pincell_multiphysics/fluid.udf)

In the .oudf file, we define boundary conditions. On the flux boundary, we will be sending a heat flux from MOOSE into NekRS, so we set the flux equal to the scratch space array, bc->usrwrk[bc->idM].

void velocityDirichletConditions(bcData * bc)
{
  bc->u = 0.0; // x-velocity
  bc->v = 0.0; // y-velocity
  bc->w = 1.0; // z-velocity
}

void scalarDirichletConditions(bcData * bc)
{
  bc->s = 0.0;
}

void scalarNeumannConditions(bcData * bc)
{
  // note: when running with Cardinal, Cardinal will allocate the usrwrk
  // array. If running with NekRS standalone (e.g. nrsmpi), you need to
  // replace the usrwrk with some other value or allocate it youself from
  // the udf and populate it with values.
  bc->flux = bc->usrwrk[bc->idM];
}
(tutorials/pincell_multiphysics/fluid.oudf)

Multiphysics Coupling

In this section, OpenMC, NekRS, and MOOSE are coupled for multiphysics modeling of an SFR pincell. This section describes all input files.

OpenMC Input Files

The neutron transport is solved using OpenMC. The input file for this portion of the physics is openmc.i. We begin by defining a number of constants and setting up the mesh mirror. For simplicity, we just use the same mesh as used in the solid application, shown in Figure 3.

inlet_T  = 573.0           # inlet temperature
power = 1e3                # total power (W)
Re = 500.0                 # Reynolds number
outlet_P = 1e6

height = 0.5               # total height of the domain
Df = 0.825e-2              # fuel diameter
pin_diameter = 0.97e-2     # pin outer diameter
pin_pitch = 1.28e-2        # pin pitch

mu = 8.8e-5                # fluid dynamic viscosity
rho = 723.6                # fluid density
Cp = 5512.0                # fluid isobaric specific heat capacity

Rf = ${fparse Df / 2.0}

flow_area = ${fparse pin_pitch * pin_pitch - pi * pin_diameter * pin_diameter / 4.0}
wetted_perimeter = ${fparse pi * pin_diameter}
hydraulic_diameter = ${fparse 4.0 * flow_area / wetted_perimeter}

U_ref = ${fparse Re * mu / rho / hydraulic_diameter}
mdot = ${fparse rho * U_ref * flow_area}
dT = ${fparse power / mdot / Cp}

[Mesh]
  [solid]
    type = FileMeshGenerator
    file = solid_in.e
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Next, we define a number of auxiliary variables to be used for diagnostic purposes. With the exception of the FluidDensityAux, none of the following variables are necessary for coupling, but they will allow us to visualize how data is mapped from OpenMC to the mesh mirror. The FluidDensityAux auxiliary kernel on the other hand is used to compute the fluid density, given the temperature variable temp (into which we will write the MOOSE and NekRS temperatures, into different regions of space). Note that we will not send fluid density from NekRS to OpenMC, because the NekRS model uses an incompressible Navier-Stokes model. But to a decent approximation, the fluid density can be approximated solely as a function of temperature using the SodiumSaturationFluidProperties (so named because these properties represent sodium properties at saturation temperature).

[AuxVariables]
# These auxiliary variables are all just for visualizing the solution and
# the mapping - none of these are part of the calculation sequence

  [material_id]
    family = MONOMIAL
    order = CONSTANT
  []
  [cell_temperature]
    family = MONOMIAL
    order = CONSTANT
  []
  [cell_density]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [material_id]
    type = CellMaterialIDAux
    variable = material_id
  []
  [cell_temperature]
    type = CellTemperatureAux
    variable = cell_temperature
  []
  [cell_density]
    type = CellDensityAux
    variable = cell_density
  []
  [density]
    type = FluidDensityAux
    variable = density
    p = ${outlet_P}
    T = nek_temp
    fp = sodium
    execute_on = 'INITIAL TIMESTEP_END'
  []
[]

[FluidProperties]
  [sodium]
    type = SodiumSaturationFluidProperties
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Next, the [Problem] and [Tallies] blocks define all the parameters related to coupling OpenMC to MOOSE. We will send temperature to OpenMC from blocks 2 and 3 (which represent the solid regions) and we will send temperature and density to OpenMC from block 1 (which represents the fluid region). We add a CellTally to tally the heat source in the fuel.

For this problem, the temperature that gets mapped into OpenMC is sourced from two different applications, which we can customize using the temperature_variables and temperature_blocks parameters. Later in the Transfers block, all data transfers from the sub-applications will write into either solid_temp or nek_temp.

Finally, we provide some additional specifications for how to run OpenMC. We set the number of batches and various triggers that will automatically terminate the OpenMC solution when reaching less than 2% maximum relative uncertainty in the fission power taly and 7.5E-4 standard deviation in kk.

[Problem]
  type = OpenMCCellAverageProblem

  power = ${power}
  scaling = 100.0
  density_blocks = '1'
  cell_level = 0

  # This automatically creates these variables and will read from the non-default choice of 'temp'
  temperature_variables = 'solid_temp; nek_temp'
  temperature_blocks = '2 3;        1'

  relaxation = robbins_monro

  # Set some parameters for when we terminate the OpenMC solve in each iteration;
  # this will run a minimum of 30 batches, and after that, terminate once reaching
  # the specified std. dev. of k and rel. err. of the fission tally
  inactive_batches = 20
  batches = 30
  k_trigger = std_dev
  k_trigger_threshold = 7.5e-4
  batch_interval = 50
  max_batches = 1000

  [Tallies]
    [heat_source]
      type = CellTally
      blocks = '2'
      name = heat_source

      check_equal_mapped_tally_volumes = true

      trigger = rel_err
      trigger_threshold = 2e-2
      output = unrelaxed_tally_std_dev
    []
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Next, we set up some initial conditions for the various fields used for coupling.

[ICs]
  [nek_temp]
    type = FunctionIC
    variable = nek_temp
    function = temp_ic
  []
  [solid_temp]
    type = FunctionIC
    variable = solid_temp
    function = temp_ic
  []
  [heat_source]
    type = ConstantIC
    variable = heat_source
    block = '2'
    value = ${fparse power / (pi * Rf * Rf * height)}
  []
[]

[Functions]
  [temp_ic]
    type = ParsedFunction
    expression = '${inlet_T} + z / ${height} * ${dT}'
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Next, we create a MOOSE heat conduction sub-application, and set up transfers of data between OpenMC and MOOSE. These transfers will send solid temperature and fluid temperature from MOOSE up to OpenMC, and a power distribution to MOOSE.

[MultiApps]
  [bison]
    type = TransientMultiApp
    input_files = 'bison.i'
    execute_on = timestep_begin
    sub_cycling = true
  []
[]

[Transfers]
  [solid_temp_to_openmc]
    type = MultiAppGeneralFieldShapeEvaluationTransfer
    source_variable = T
    variable = solid_temp
    from_multi_app = bison
  []
  [source_to_bison]
    type = MultiAppCopyTransfer
    source_variable = heat_source
    variable = power
    to_multi_app = bison
  []
  [temp_from_nek]
    type = MultiAppGeneralFieldShapeEvaluationTransfer
    source_variable = nek_temp
    from_multi_app = bison
    variable = nek_temp
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Finally, we will use a Transient executioner and add a number of postprocessors for diagnostic purposes.

[Outputs]
  exodus = true
  csv = true
[]

[Executioner]
  type = Transient
  dt = 0.5
  num_steps = 10
[]

[Postprocessors]
  [max_tally_rel_err]
    type = TallyRelativeError
    value_type = max
  []
  [k]
    type = KEigenvalue
  []
  [k_std_dev]
    type = KStandardDeviation
  []
[]
(tutorials/pincell_multiphysics/openmc.i)

Solid Input Files

The conservation of solid energy is solved using the MOOSE heat transfer module. The input file for this portion of the physics is bison.i. We begin by defining a number of constants and setting the mesh.

inlet_T  = 573.0           # inlet temperature
power = 250                # total power (W)
Re = 500.0                 # Reynolds number

height = 0.5               # total height of the domain
Df = 0.825e-2              # fuel diameter
pin_diameter = 0.97e-2     # pin outer diameter
pin_pitch = 1.28e-2        # pin pitch

mu = 8.8e-5                # fluid dynamic viscosity
rho = 723.6                # fluid density
Cp = 5512.0                # fluid isobaric specific heat capacity

Rf = ${fparse Df / 2.0}

flow_area = ${fparse pin_pitch * pin_pitch - pi * pin_diameter * pin_diameter / 4.0}
wetted_perimeter = ${fparse pi * pin_diameter}
hydraulic_diameter = ${fparse 4.0 * flow_area / wetted_perimeter}

U_ref = ${fparse Re * mu / rho / hydraulic_diameter}
mdot = ${fparse rho * U_ref * flow_area}
dT = ${fparse power / mdot / Cp}

[Mesh]
  [solid]
    type = FileMeshGenerator
    file = solid_in.e
  []
[]
(tutorials/pincell_multiphysics/bison.i)

Because some blocks in the solid mesh aren't actually used in the solid solve (i.e. the fluid block we will use to receive fluid temperature and density from NekRS), we need to explicitly tell MOOSE to not throw errors related to checking for material properties on every mesh block.

[Problem]
  type = FEProblem
  material_coverage_check = false
[]
(tutorials/pincell_multiphysics/bison.i)

Next, we set up a nonlinear variable T to represent solid temperature and create kernels representing heat conduction with a volumetric heating in the pellet region. In the fluid region, we need to use a NullKernel to indicate that no actual solve happens on this block. On the cladding surface, we will impose a Dirichlet boundary condition given the NekRS fluid temperature. Finally, we set up material properties for the solid blocks using HeatConductionMaterial.

[Variables]
  [T]
    initial_condition = ${inlet_T}
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
    block = '2 3'
  []
  [source]
    type = CoupledForce
    variable = T
    v = power
    block = '2'
  []
  [null]
    type = NullKernel
    variable = T
    block = '1'
  []
[]

[BCs]
  [pin_outer]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5'
  []
[]

[Materials]
  [uo2]
    type = HeatConductionMaterial
    thermal_conductivity = 5.0
    block = '2'
  []
  [clad]
    type = HeatConductionMaterial
    thermal_conductivity = 20.0
    block = '3'
  []
[]
(tutorials/pincell_multiphysics/bison.i)

Next, we declare auxiliary variables to be used for:

  • coupling to NekRS (to receive the NekRS temperature, nek_temp)

  • computing the pin surface heat flux (to send heat flux flux to NekRS)

  • power to represent the volumetric heating received from OpenMC

On each MOOSE-NekRS substep, we will run MOOSE first. For the very first time step, this means we should set an initial condition for the NekRS fluid temperature, which we simply set to a linear function of height. Finally, we create a DiffusionFluxAux to compute the heat flux on the pin surface.

[AuxVariables]
  [nek_temp]
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
  [power]
    family = MONOMIAL
    order = CONSTANT
    initial_condition = ${fparse power / (pi * Rf * Rf * height)}
  []
[]

[Functions]
  [axial_fluid_temp]
    type = ParsedFunction
    expression = '${inlet_T} + z / ${height} * ${dT}'
  []
[]

[ICs]
  [nek_temp]
    type = FunctionIC
    variable = nek_temp
    function = axial_fluid_temp
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5'
  []
[]
(tutorials/pincell_multiphysics/bison.i)

Next, we create a NekRS sub-application and set up the data transfers between MOOSE and NekRS. There are four transfers - three are related to sending the temperature and heat flux between MOOSE and NekRS, and the fourth is related to a performance optimization in the NekRS wrapping that will only interpolate data to/from NekRS at the synchronization points with the application "driving" NekRS (in this case, MOOSE heat conduction).

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    execute_on = timestep_end
    sub_cycling = true
  []
[]

[Transfers]
  [temperature]
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temp
    from_multi_app = nek
    variable = nek_temp
  []
  [flux]
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = avg_flux
    from_boundaries = '5'
  []
  [flux_integral]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [send]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = send
    to_multi_app = nek
  []
[]
(tutorials/pincell_multiphysics/bison.i)

Next, we set up a number of postprocessors, both for normalizing the total power sent from MOOSE to NekRS, as well as a few diagnostic terms.

[Postprocessors]
  [send]
    type = Receiver
    default = 1.0
  []
  [flux_integral]
    # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5'
  []
  [power]
    type = ElementIntegralVariablePostprocessor
    variable = power
    block = '2'
    execute_on = 'transfer initial'
  []
  [max_T_solid]
    type = ElementExtremeValue
    variable = T
    block = '2 3'
  []
[]
(tutorials/pincell_multiphysics/bison.i)

Finally, we set up the MOOSE heat conduction solver to use a Transient exeuctioner and specify the output format. Important to note here is that a user-provided choice of M will determine how many NekRS time steps are run for each MOOSE time step.

[Executioner]
  type = Transient
  dt = ${fparse M * t_nek * dt0}
  num_steps = 100

  nl_abs_tol = 1e-8
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'
[]

[Outputs]
  exodus = true
  hide = 'power flux_integral send'
[]
(tutorials/pincell_multiphysics/bison.i)

Fluid Input Files

The fluid mass, momentum, and energy transport physics are solved using NekRS. The input file for this portion of the physics is nek.i. We begin by defining a number of constants and by setting up the NekRSMesh mesh mirror. Because we are coupling NekRS via boundary heat transfer to MOOSE, but via volumetric temperature and densities to OpenMC, we need to use a combined boundary and volumetric mesh mirror, so both boundary and volume = true are provided. Because this problem is set up in non-dimensional form, we also need to rescale the mesh to match the units expected by our solid and OpenMC input files.

inlet_T  = 573.0           # inlet temperature
power = 250                # total power (W)
Re = 500.0                 # Reynolds number

pin_diameter = 0.97e-2     # pin outer diameter
pin_pitch = 1.28e-2        # pin pitch

mu = 8.8e-5                # fluid dynamic viscosity
rho = 723.6                # fluid density
Cp = 5512.0                # fluid isobaric specific heat capacity

flow_area = ${fparse pin_pitch * pin_pitch - pi * pin_diameter * pin_diameter / 4.0}
wetted_perimeter = ${fparse pi * pin_diameter}
hydraulic_diameter = ${fparse 4.0 * flow_area / wetted_perimeter}

U_ref = ${fparse Re * mu / rho / hydraulic_diameter}
mdot = ${fparse rho * U_ref * flow_area}
dT = ${fparse power / mdot / Cp}

[Mesh]
  type = NekRSMesh
  boundary = '1'
  scaling = ${hydraulic_diameter}
  volume = true
[]
(tutorials/pincell_multiphysics/nek.i)

The bulk of the NekRS wrapping is specified with NekRSProblem. The NekRS input files are in non-dimensional form, whereas all other coupled applications use dimensional units. The various *_ref and *_0 parameters define the characteristic scales that were used to non-dimensionalize the NekRS input. In order to simplify the input file, we know a priori that OpenMC will not be sending a heat source to NekRS, so we set has_heat_source = false so that we don't need to add a dummy heat source kernel to the fluid.oudf file. If we had volumetric heating in the fluid, then we would instead send a heating term into NekRS, but this is neglected for this example.

[Problem]
  type = NekRSProblem
  casename = 'fluid'

  [Dimensionalize]
    L = ${hydraulic_diameter}
    T = ${inlet_T}
    U = ${U_ref}
    dT = ${dT}
    rho = ${rho}
    Cp = ${Cp}
  []

  has_heat_source = false
  synchronization_interval = parent_app
[]
(tutorials/pincell_multiphysics/nek.i)

Then, we simply set up a Transient executioner with the NekTimeStepper. For postprocessing purposes, we also create two postprocessors to evaluate the average outlet temperature and the maximum fluid temperature. Finally, in order to not overly saturate the screen output, we will only write the Exodus output files and print to the console every 10 Nek time steps.

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  interval = 10
[]
(tutorials/pincell_multiphysics/nek.i)

Execution

To run the input files,

mpiexec -np 4 cardinal-opt -i openmc.i

This will produce a number of output files,

  • openmc_out.e, OpenMC simulation results, mapped to a mesh mirror

  • openmc_out_bison0.e, MOOSE heat conduction simulation results

  • openmc_out_bison0_nek0.e, NekRS simulation results, mapped to a mesh mirror

  • fluid0.f*, NekRS output files

Figure 5 shows the temperature (a) imposed in OpenMC (the output of the CellTemperatureAux) auxiliary kernel; (b) the NekRS fluid temperature; and (c) the MOOSE solid temperature.

Figure 5: Temperatures predicted by NekRS and BISON (middle, right), and what is imposed in OpenMC (left). All images are shown on the same color scale.

The OpenMC power distribution is shown in Figure 6. The small variations of sodium density with temperature cause the power distribution to be fairly symmetric in the axial direction.

Figure 6: OpenMC predicted power distribution

Finally, Figure 7 shows the fluid and solid temperatures (a) with both phases shown and (b) with just the fluid region highlighted. The very lower power in this demonstration results in fairly small temperature gradients in the fuel, but what is important to note is the coupled solution captures typical conjugate heat transfer temperature distributions in rectangular pincells. You can always extend this tutorial to turbulent conditions and increase the power to display temperature distributions more characteristic of real nuclear systems.

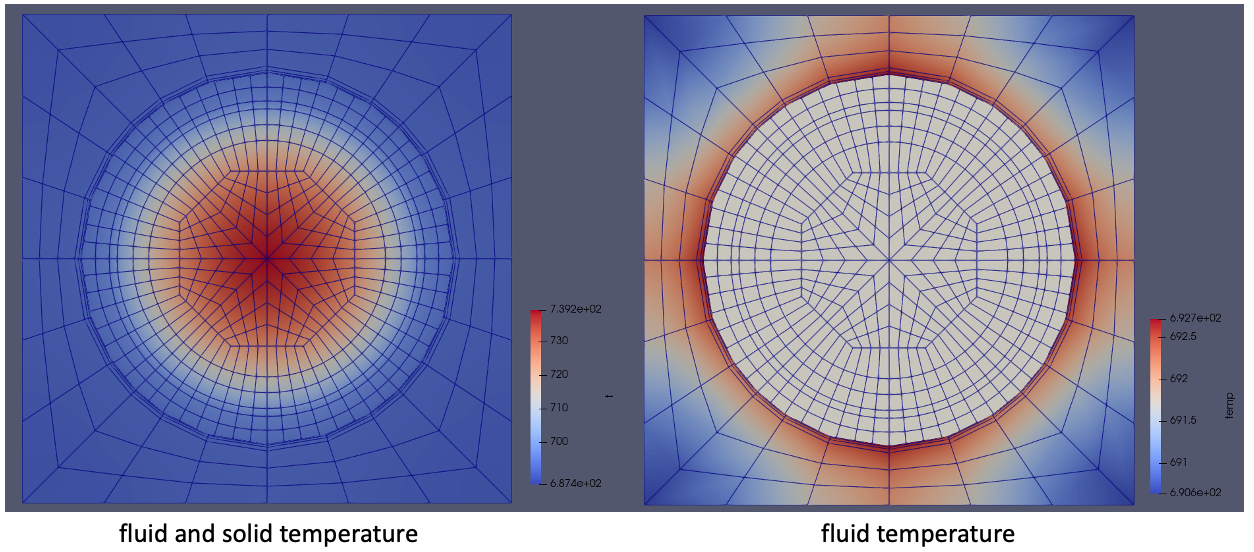
Figure 7: Temperatures predicted by NekRS and BISON on the axial midplane.

In this tutorial, OpenMC, MOOSE, and NekRS each used their own time step. You may want to try re-running this tutorial using different time step sizes in the OpenMC and MOOSE heat conduction input files, to explore how to sub-cycle these codes together.