UO Pebbles
In this tutorial, you will learn how to:
Couple OpenMC via temperature and heat source feedback to MOOSE for pebbles
Establish coupling between OpenMC and MOOSE for nested universe OpenMC models
Couple OpenMC solves in units of centimeters with MOOSE solves in units of meters
Repeat the same mesh tally several times throughout the OpenMC domain
To access this tutorial,
cd cardinal/tutorials/pebbles
Geometry and Computational Models
The geometry and computational model for this case consists of a vertical "stack" of three solid UO pebbles, each of 1.5 cm radius. The pebble centers are located at cm, cm, and cm. FLiBe coolant occupies the space around the pebbles. Heat is produced in the pebbles; we assume the total power is 1500 W.
While "pebbles" in nuclear applications typically refer to TRISO fuel geometries, this tutorial only considers homogeneous pebbles so as to serve as a stepping stone to modeling heterogeneous TRISO geometries in a later tutorial. Here, we first emphasize important features of the OpenMC wrapping having to do with lattices and unstructured mesh tallies.
Heat Conduction Model
The MOOSE heat transfer module is used to solve for steady-state heat conduction,
(1)
where is the solid thermal conductivity, is the solid temperature, and is a volumetric heat source in the solid.
The solid mesh is shown in Figure 1. The pebble surface is sideset 0. The MOOSE solid problem is set up with a length unit of meters, which is convenient for heat transfer applications because material properties for thermal-fluids physics are almost always given in SI units. Further, many MOOSE physics modules inherently assume SI units, such as the fluid property module and solid property module.
Figure 1: Mesh for solid domain
Because heat transfer and fluid flow in the FLiBe is not modeled in this example, heat removal by the fluid is approximated by setting the outer surface of the pebble to a convection boundary condition,
(2)
where W/m/K and is set to a function linearly ranging from 650°C at cm to 750°C at cm. In this example, the MOOSE heat transfer module will be run first. The initial solid temperature is set to 650°C and the heat source to zero.
OpenMC Model
The OpenMC model is built using CSG; we will leverage the lattice feature in OpenMC to repeat a universe in a structured manner throughout the domain. Here, the universe consists of a single pebble and surrounding FLiBe, which is repeated three times throughout the geometry. The overall domain is enclosed in a box with - width of 44 cm and height of 12 cm. All boundaries of this box are reflecting.
OpenMC's Python API is used to create the pebbles model with the script shown below. First, we define materials for the various regions and create the geometry. We create a universe consisting of a single pebble, and then repeat that universe three times in a lattice. Because we have one cell per pebble, each pebble will receive a single temperature from MOOSE. The cell level is 1 because the pebble lattice is nested once with respect to the highest level, and we want to apply feedback to each pebble individually. If we were to specify level zero in the geometry, we would apply feedback to the main_cell, which would apply temperature feedback across the problem globally. The OpenMC geometry as produced via plots is shown in Figure 2.
import openmc
import numpy as np
# Add materials for the pebbles and the FLiBe
uo2 = openmc.Material()
uo2.set_density('g/cc', 10.0)
uo2.add_element('U', 1.0, enrichment=5.0)
uo2.add_element('O', 2.0)
enrichment_li7 = 0.99995
flibe = openmc.Material(name='2LiF-BeF2')
flibe.set_density('kg/m3', 1960)
flibe.add_nuclide('Li7', 2.0*enrichment_li7)
flibe.add_nuclide('Li6', 2.0*(1 - enrichment_li7))
flibe.add_element('Be', 1.0)
flibe.add_element('F', 4.0)
mats = openmc.Materials([uo2, flibe])
mats.export_to_xml()
model = openmc.model.Model()
# create a universe containing the repeatable universe of
# a single pebble plus surrounding flibe
R = 1.5
L = 4.0
sphere_surface = openmc.Sphere(r=R, name='Sphere surface')
flibe_surface = openmc.model.RectangularPrism(L, L, boundary_type='reflective')
sphere_cell = openmc.Cell(fill=uo2, region=-sphere_surface, name='Pebble')
flibe_cell = openmc.Cell(fill=flibe, region=+sphere_surface & -flibe_surface, name='Flibe')
repeatable_univ = openmc.Universe(cells=[sphere_cell, flibe_cell])
outer_cell = openmc.Cell(fill=flibe, region=+sphere_surface & -flibe_surface, name='Outside')
outer_univ = openmc.Universe(cells=[outer_cell])
# create a lattice to repeat the pebble + flibe universe
N = 3
lattice = openmc.RectLattice()
lattice.lower_left = (-L/2.0, -L/2.0, 0)
lattice.pitch = (L, L, L)
lattice.universes = np.full((N, 1, 1), repeatable_univ)
lattice.outer = outer_univ
# create the surfaces that will bound the lattice
top = openmc.ZPlane(z0=N*L, boundary_type='reflective')
bottom = openmc.ZPlane(z0=0.0, boundary_type='reflective')
main_cell = openmc.Cell(fill=lattice, region=-flibe_surface & +bottom & -top, name='Main cell')
model.geometry = openmc.Geometry([main_cell])
model.geometry.export_to_xml()
# Finally, define some run settings
model.settings = openmc.Settings()
model.settings.batches = 1000
model.settings.inactive = 100
model.settings.particles = 10000
lower_left = (-L, -L, 0)
upper_right = (L, L, N*L)
uniform_dist = openmc.stats.Box(lower_left, upper_right, only_fissionable=True)
model.settings.source = openmc.IndependentSource(space=uniform_dist)
model.settings.temperature = {'default': 650.0 + 273.15,
'method': 'interpolation',
'multipole': False,
'tolerance': 1000.0,
'range': (294.0, 1600.0)}
model.settings.export_to_xml()
# create some plots for making images in the tutorial
height = N*L
plot1 = openmc.Plot()
plot1.filename = 'plot1'
plot1.width = (L, height)
plot1.basis = 'xz'
plot1.origin = (0.0, 0.0, height/2.0)
plot1.pixels = (100, 300)
plot1.color_by = 'cell'
plot2 = openmc.Plot()
plot2.filename = 'plot2'
plot2.width = (L, L)
plot2.basis = 'xy'
plot2.origin = (0.0, 0.0, 2.0)
plot2.pixels = (100, 100)
plot2.color_by = 'cell'
plots = openmc.Plots([plot1, plot2])
plots.export_to_xml()
Figure 2: OpenMC geometry (colored by cell ID)
As you can see, there are only two unique cell IDs. This problem is built using distributed cells, meaning a cell with the same ID appears multiple times in the geometry; each time the cell is repeated, we assign a new instance to that cell. So, the three pebbles are represented as:
Cell ID 1, instance 0
Cell ID 1, instance 1
Cell ID 1, instance 2
and the FLiBe region is represented as:
Cell ID 2, instance 0
Cell ID 2, instance 1
Cell ID 2, instance 2
Because OpenMC runs after the MOOSE heat transfer module, initial conditions are only required for the FLiBe temperature, which is set to 650°C. Because there is no density feedback in this example, the densities initially imposed in the OpenMC model remain fixed at the values set in the OpenMC input files.
To create the XML files required to run OpenMC, run the script:
python make_openmc_model.py
Multiphysics Coupling
In this section, OpenMC and MOOSE are coupled for heat source and temperature feedback for the solid regions of a stack of three pebbles. The following sub-sections describe these files.
Solid Input Files
The solid phase is solved with the MOOSE heat transfer module, and is described in the solid.i input. We set up the mesh using the CombinerGenerator to translate a single sphere mesh to multiple locations.
[Mesh]
[pebble]
type = SphereMeshGenerator
nr = 2
radius = 0.015
[]
[repeat]
type = CombinerGenerator
inputs = pebble
positions = '0 0 0.02
0 0 0.06
0 0 0.10'
[]
[]
Next, we define the temperature variable, temp, and specify the governing equations and boundary conditions that we will apply. We set the thermal conductivity of the pebbles to 50 W/m/K.
[Variables]
[temp]
initial_condition = ${T_fluid}
[]
[]
[Kernels]
[hc]
type = HeatConduction
variable = temp
[]
[heat]
type = CoupledForce
variable = temp
v = heat_source
[]
[]
[Functions]
[T_fluid]
type = ParsedFunction
expression = '${T_fluid}+z*1000'
[]
[]
[BCs]
[surface]
type = ConvectiveFluxFunction
T_infinity = T_fluid
coefficient = 1000.0
variable = temp
boundary = '0'
[]
[]
[Materials]
[k]
type = GenericConstantMaterial
prop_values = '50.0'
prop_names = 'thermal_conductivity'
[]
[]
The heat source received from OpenMC is stored in the heat_source auxiliary variable.
[AuxVariables]
[heat_source]
family = MONOMIAL
order = CONSTANT
[]
[]
Finally, we specify that we will run a OpenMC as a sub-application, with data transfers of heat source from OpenMC and temperature to OpenMC and use a transient executioner.
[MultiApps]
[openmc]
type = TransientMultiApp
input_files = 'openmc.i'
execute_on = timestep_end
[]
[]
[Transfers]
[heat_source_from_openmc]
type = MultiAppGeneralFieldNearestLocationTransfer
from_multi_app = openmc
variable = heat_source
source_variable = heat_source
from_postprocessors_to_be_preserved = heat_source
to_postprocessors_to_be_preserved = source_integral
[]
[temp_to_openmc]
type = MultiAppGeneralFieldShapeEvaluationTransfer
to_multi_app = openmc
variable = temp
source_variable = temp
[]
[]
[Postprocessors]
[source_integral]
type = ElementIntegralVariablePostprocessor
variable = heat_source
execute_on = transfer
[]
[max_T]
type = NodalExtremeValue
variable = temp
[]
[]
[Executioner]
type = Transient
petsc_options_iname = '-pc_type -pc_hypre_type'
num_steps = 3
petsc_options_value = 'hypre boomeramg'
nl_abs_tol = 1e-10
[]
[Outputs]
exodus = true
[]
Neutronics Input Files
The neutronics physics is solved over the entire domain using OpenMC. The OpenMC wrapping is described in the openmc.i input file. We begin by defining a mesh mirror on which OpenMC will receive temperature from the coupled MOOSE application, and on which OpenMC will write the fission heat source.
[Mesh]
[pebble]
type = SphereMeshGenerator
nr = 2
radius = 0.015
[]
[repeat]
type = CombinerGenerator
inputs = pebble
positions = '0 0 0.02
0 0 0.06
0 0 0.10'
[]
[]
Even though OpenMC solves in units of centimeters, the mesh put in the [Mesh] block must use the same units as in the coupled MOOSE application. Otherwise, the transfers used to send temperature and heat source to/from OpenMC will not map to the correct elements across applications. For instance, if the [Mesh] in the solid.i input were in units of meters, but the [Mesh] in the openmc.i input were in units of centimeters, then a point m in solid.i would get mapped to the node closest to the point cm in openmc.i (when we actually want the point to map to cm).
Cardinal will also automatically output a variable named cell_id (CellIDAux) and a variable named cell_instance ( CellInstanceAux) to show the spatial mapping. We also define a CellTemperatureAux to show the OpenMC volume-averaged temperatures as they map to the [Mesh].
[AuxVariables]
[cell_temperature]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[cell_temperature]
type = CellTemperatureAux
variable = cell_temperature
[]
[]
The [Problem] and [Tallies] blocks are then used to specify the OpenMC wrapping. We define a total power of 1500 W, and indicate that we'd like to add a CellTally on block 0, which corresponds to the pebbles. The cell tally setup in Cardinal will then automatically add a tally for each unique cell ID+instance combination. Because the repeated pebble cells we'd like to tally are repeated in the lattice nested one level below the root universe, we set the cell_level = 1.
[Problem]
type = OpenMCCellAverageProblem
verbose = true
power = 1500.0
temperature_blocks = '0'
cell_level = 1
scaling = 100.0
[Tallies]
[heat_source]
type = CellTally
blocks = '0'
name = heat_source
[]
[]
[]
The scaling parameter is used to indicate a multiplicative factor that should be applied to the [Mesh] in order to get to units of centimeters. Because the [Mesh] is in units of meters, we set scaling = 100.0. This scaling factor is applied within the OpenMCCellAverageProblem::findCell routine that maps MOOSE elements to OpenMC cells - no actual changes are made to the mesh in the [Mesh] block. The scaling is also applied to ensure that the heat source is on the correct per-unit-volume scale that is expected by the [Mesh].
Finally, we set a transient executioner, specify an Exodus output, and define several postprocessors.
[Executioner]
type = Transient
[]
[Outputs]
exodus = true
csv = true
[]
[Postprocessors]
[heat_source]
type = ElementIntegralVariablePostprocessor
variable = heat_source
[]
[max_tally_rel_err]
type = TallyRelativeError
[]
[k]
type = KEigenvalue
[]
[]
Execution and Postprocessing
To run the coupled calculation,
mpiexec -np 2 cardinal-opt -i solid.i --n-threads=2
This will run both MOOSE and OpenMC with 8 MPI processes and 2 OpenMP threads per rank. When the simulation has completed, you will have created a number of different output files:
solid_out.e, an Exodus file with the solid mesh and solutionsolid_out_openmc0.e, an Exodus file with the OpenMC solution and the data that was ultimately transferred in/out of OpenMC
First, let's examine how the mapping between OpenMC and MOOSE was established. When we run with verbose = true, you will see the following mapping information displayed:
===================> MAPPING FROM OPENMC TO MOOSE <===================
T: # elems providing temperature feedback
T+rho: # elems providing temperature and density feedback
Other: # elems which do not provide feedback to OpenMC
(but receives a cell tally from OpenMC)
Mapped Vol: volume of MOOSE elems each cell maps to
Actual Vol: OpenMC cell volume (computed with 'volume_calculation')
--------------------------------------------------------------------------
| Cell | T | T+rho | Other | Mapped Vol | Actual Vol |
--------------------------------------------------------------------------
| 1, instance 0 (of 3) | 448 | 0 | 0 | 1.322e-05 | |
| 1, instance 1 (of 3) | 448 | 0 | 0 | 1.322e-05 | |
| 1, instance 2 (of 3) | 448 | 0 | 0 | 1.322e-05 | |
--------------------------------------------------------------------------
The three cells representing the pebbles are mapped to the corresponding MOOSE elements for each pebble. Shown below is the heat source computed by OpenMC, along with the temperature computed by MOOSE (before and after being averaged and sent to OpenMC cells). The temperature is shown on a cut plane through the centers of the pebbles; because one temperature is set for each pebble, the temperature in OpenMC for each pebble is an average over the pebble.
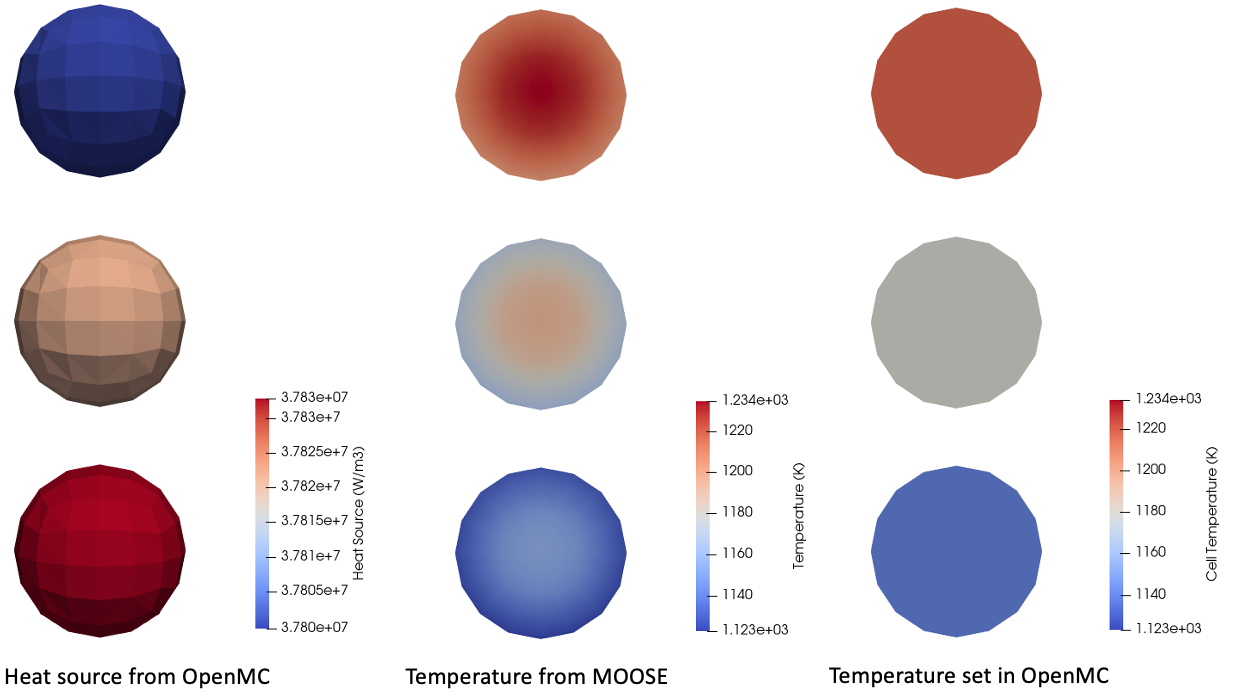
Figure 3: Heat source and temperature computed by a coupled OpenMC-MOOSE model of pebbles
You can confirm that the scaling factor was applied correctly by comparing the heat_source postprocessor, of the volume integral of the heat source, with the total power specified in OpenMCCellAverageProblem - both are equal to 1500 W. If the integral is off by a factor of from the power, then you know right away that the scaling was not applied correctly.
Repeated Mesh Tallies
Many geometries of interest to nuclear reactor analysis contain repeated structures - such as pebbles in a Pebble Bed Reactor (PBR) or pincells in a Light Water Reactor (LWR). In this section, we build upon our model by using an unstructured mesh tally, with a single unstructured mesh translated multiple times throughout the OpenMC geometry. In other words, if the memory used to store an unstructured mesh of a single pebble is 500 kB, then an unstructured mesh tally of 300,000 pebbles still only requires a mesh storage of 500 kB (as opposed to generating a mesh of 300,000 pebbles that is ~150 GB).
The files for this stage of the coupling are the solid_um.i and openmc_um.i inputs in the tutorials/pebbles directory. For the solid, we simply need to swap out the sub-application to point to a different OpenMC input file.
[MultiApps]
[openmc]
type = TransientMultiApp
input_files = 'openmc_um.i'
execute_on = timestep_end
[]
[]
We also use a finer solid pebble heat conduction mesh to provide an example of the case where the OpenMC [Mesh] block differs from the mesh used in the coupled MOOSE application. To do this, we increase nr to add more radial discretization.
[Mesh]
[pebble]
type = SphereMeshGenerator
nr = 4
radius = 0.015
[]
[rotate]
# we can rotate the pebble, MOOSEs mesh transfers still handle the transfer properly
type = TransformGenerator
input = pebble
transform = rotate
vector_value = '0.5 0.2 0.2'
[]
[repeat]
type = CombinerGenerator
inputs = rotate
positions = '0 0 0.02
0 0 0.06
0 0 0.10'
[]
[]
For the OpenMC wrapping, the only changes required are that we change the added tally to a MeshTally, provide a mesh template with the mesh, and specify the translations to apply to replicate the mesh at the desired end positions in OpenMC's domain. For the mesh tally, let's create a mesh for a single pebble using MOOSE's mesh generators. We simply need to run the mesh.i file in --mesh-only mode:
[Mesh]
[pebble]
type = SphereMeshGenerator
nr = 2
radius = 0.015
[]
[]
cardinal-opt -i mesh.i --mesh-only
which will create a mesh file named mesh_in.e. We then list that mesh as the mesh_template in the [Tallies] block.
[Problem]
type = OpenMCCellAverageProblem
verbose = true
power = 1500.0
temperature_blocks = '0'
normalize_by_global_tally = false
cell_level = 1
scaling = 100.0
[Tallies]
[heat_source]
type = MeshTally
mesh_translations = '0 0 0.02
0 0 0.06
0 0 0.10'
mesh_template = mesh_in.e
name = heat_source
[]
[]
[]
Note that the mesh template and mesh translations must be in the same units as the [Mesh] block. In addition, because our sphere mesh does not perfectly preserve the volume of the sphere cells, we set normalize_by_global_tally to false so that we normalize only by the sum of the mesh tally. Otherwise, we would miss a small amount of power produced within the spheres, but slightly outside the faceted surface of the sphere mesh. Setting this parameter to false ensures that the tally normalization is correct in that the heat sources are normalized by a tally sum over the same tally domain in the OpenMC model.
To run this input,
mpiexec -np 2 cardinal-opt -i solid_um.i --n-threads=2
Figure 4 shows the heat source computed by OpenMC, the heat source applied in MOOSE, the temperature computed by MOOSE, and the temperature applied in OpenMC. The MOOSE transfers handle the different meshes seamlessly. The mesh translation feature allows a single pebble mesh to be translated to three individual positions in the OpenMC tally. Note that the heat sources on the OpenMC [Mesh] and on the MOOSE heat conduction mesh are shown on a different color scale - the volumetric power density on the MOOSE mesh is lower than that on the OpenMC mesh because the MOOSE mesh has a greater volume (since there is a better approximation of the sphere volume). The conservative MultiAppGeneralFieldNearestLocationTransfer conserves total integrated power.
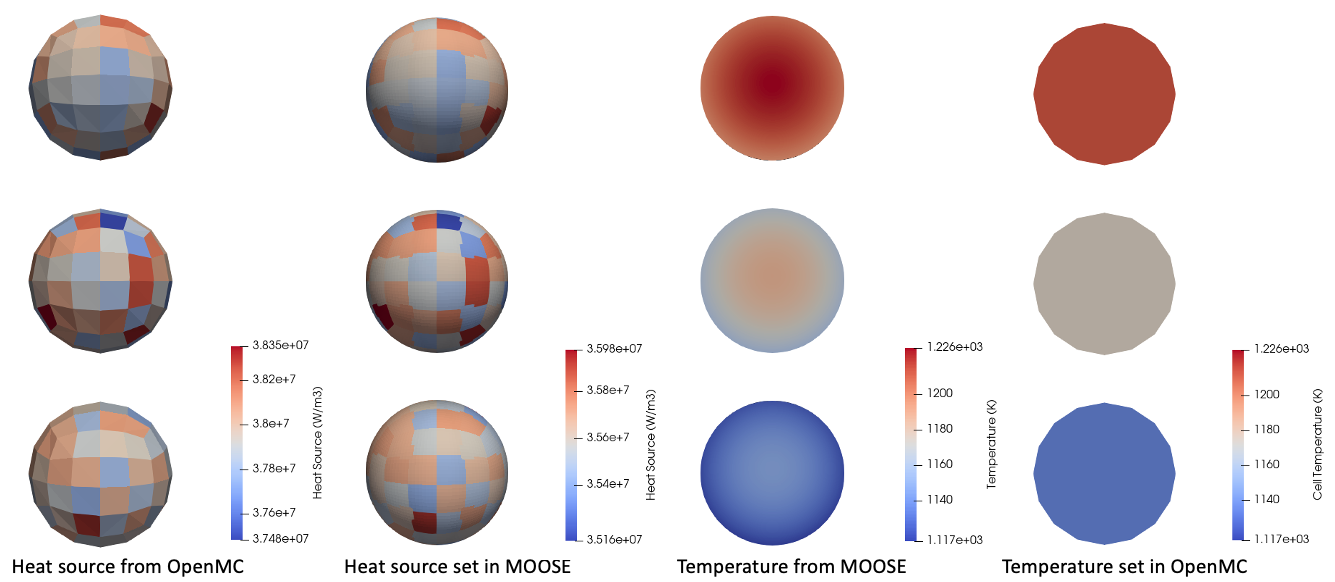
Figure 4: Temperature and heat source distributions shown on the different MOOSE and OpenMC meshes. The temperatures are shown on a slice through the centers of the pebbles.
Finally, recall that adding unstructured mesh tallies does not affect the resolution of temperature and density feedback sent to OpenMC - this resolution is controlled by the cell definitions when constructing the OpenMC input. Therefore, each pebble still receives a single temperature value from MOOSE because each pebble is represented as a single cell.