Multiphysics for a TRISO Gas-Cooled Compact
In this tutorial, you will learn how to:
Couple OpenMC, NekRS/THM, and MOOSE together for multiphysics modeling of a Tri-Structural Isotropic (TRISO) compact
Use two different MultiApp hierarchies to achieve different data transfers
Use triggers to automatically terminate the OpenMC active batches once reaching the desired statistical uncertainty
Automatically detect steady state
To access this tutorial,
cd cardinal/tutorials/gas_compact_multiphysics
This tutorial also requires you to download mesh files and a NekRS restart file from Box. Please download the files from the gas_compact_multiphysics folder here and place these within the same directory structure in tutorials/gas_compact_multiphysics.
This tutorial requires HPC resources to run the NekRS cases. You will be able to run the OpenMC-THM-MOOSE files without any special resources.
In this tutorial, we couple OpenMC to the MOOSE heat transfer module, with fluid feedback provided by either NekRS or THM,
NekRS: wall-resolved - Reynolds Averaged Navier-Stokes (RANS) equations
Thermal Hydraulics Module (THM): 1-D area-averaged Navier-Stokes equations
Two different multiapp hierarchies will be used in order to demonstrate the flexibility of the MultiApp system. The same OpenMC model can be used to provide feedback to different combinations of MOOSE applications.
In this tutorial, OpenMC receives temperature feedback from the MOOSE heat conduction module (for the solid regions) and NekRS/THM (for the fluid regions). Density feedback is provided by NekRS/THM for the fluid regions. This tutorial models a partial-height TRISO-fueled unit cell of a prismatic gas reactor assembly, and is a continuation of the conjugate heat transfer tutorial (where we coupled NekRS and MOOSE heat conduction) and the OpenMC-heat conduction tutorial (where we coupled OpenMC and MOOSE heat conduction) for this geometry.
This tutorial was developed with support from the NEAMS Thermal Fluids Center of Excellence and is described in more detail in our journal article Novak et al. (2022).
Geometry and Computational Model
The geometry consists of a TRISO-fueled gas reactor compact unit cell INL (2016). A top-down view of the geometry is shown in Figure 1. The fuel is cooled by helium flowing in a cylindrical channel of diameter . Cylindrical fuel compacts containing randomly-dispersed TRISO particles at 15% packing fraction are arranged around the coolant channel in a triangular lattice. The TRISO particles use a conventional design that consists of a central fissile uranium oxycarbide kernel enclosed in a carbon buffer, an inner Pyrolitic Carbon (PyC) layer, a silicon carbide layer, and finally an outer PyC layer. The geometric specifications are summarized in Table 1. Heat is produced in the TRISO particles to yield a total power of 38 kW.
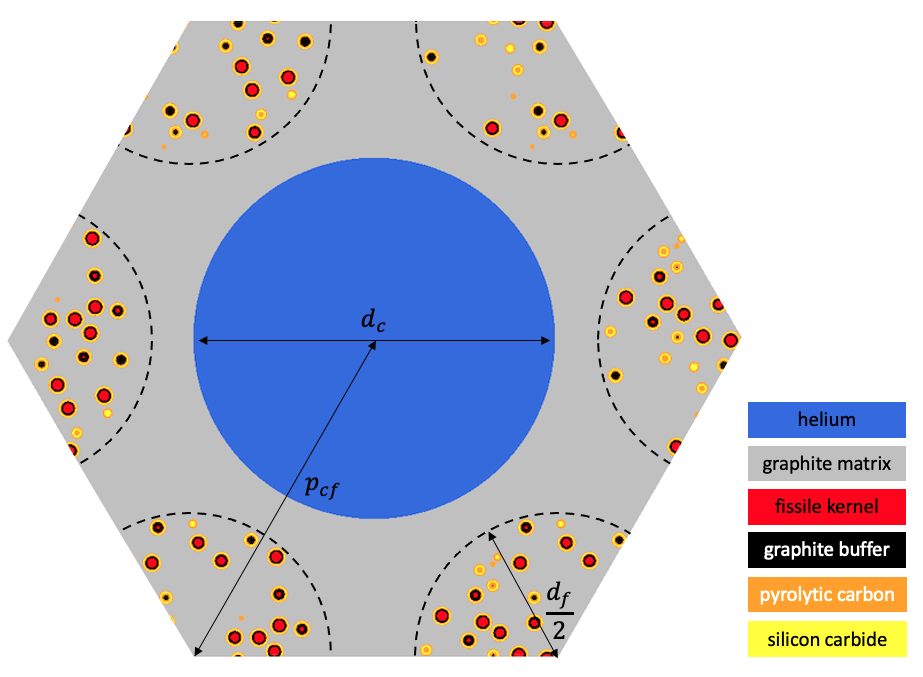
Figure 1: TRISO-fueled gas reactor compact unit cell
Table 1: Geometric specifications for a TRISO-fueled gas reactor compact
| Parameter | Value (cm) |
|---|---|
| Coolant channel diameter, | 1.6 |
| Fuel compact diameter, | 1.27 |
| Fuel-to-coolant center distance, | 1.88 |
| Height | 160 |
| TRISO kernel radius | 214.85e-4 |
| Buffer layer radius | 314.85e-4 |
| Inner PyC layer radius | 354.85e-4 |
| Silicon carbide layer radius | 389.85e-4 |
| Outer PyC layer radius | 429.85e-4 |
Two different MultiApp hierarchies are used:
A "single stack" design where each application has either a single "parent" application or a single "child" application
A "tree" design where each application has a single "parent" application, but multiple "child" applications
Figure 2 shows a conceptual depiction of these hierarchies. We will describe these in greater detail later, but introduce them here to assist with describing a few aspects of the single-physics models. The circled numbers indicate the order in which the applications run.
Solid lines depict transfers that occur directly from application to application , or between the source and receiver of that field. Dashed lines, on the other hand, depict transfers that do not occur directly between the source and receiver of the field - for instance, in the "single stack" hierarchy, the NekRS application can only communicate data with it's immediate parent application. Therefore, to send fluid density and temperature from NekRS to OpenMC, there are actually two transfers - 1) sending fluid density and temperature from NekRS to the MOOSE heat transfer module, and 2) sending fluid density and temperature from the MOOSE heat transfer module to OpenMC.
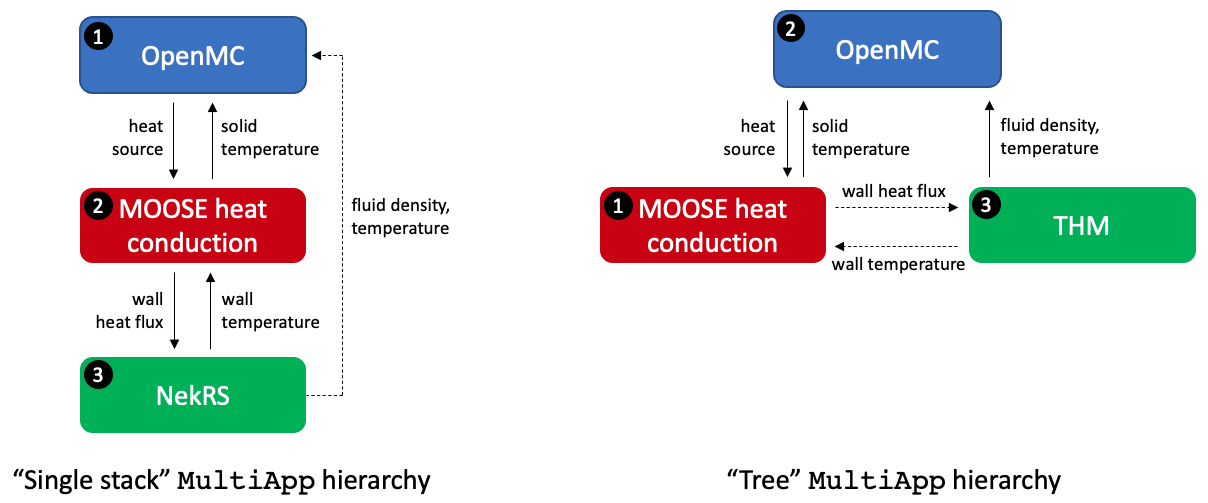
Figure 2: MultiApp hierarchies used in this tutorial; data transfers are shown with solid and dashed lines. Solid lines indicate transfers that occur directly from application A to application B, while dashed lines show transfers that have to first pass through an intermediate application to get to the eventual target application.
Conversely, with the "tree" hierarhcy, MOOSE MultiApps communicate with parent/child applications. Therefore, all data communicated between the MOOSE heat transfer module and THM actually has to first pass through their common parent application before reaching the desired target application.
In the time since we originally developed this tutorial, MOOSE has been extended to support sibling transfers, which would allow MOOSE and THM to communicate data directly to one another (in the "tree" hierarchy shown in Figure 2).
OpenMC Model
The OpenMC model is built using Constructive Solid Geometry (CSG). The TRISO positions are sampled using the Random Sequential Addition (RSA) algorithm in OpenMC. OpenMC's Python Application Programming Interface (API) is used to create the model with the script shown below. First, we define materials. Next, we create a single TRISO particle universe consisting of the five layers of the particle and an infinite extent of graphite filling all other space. We then pack pack uniform-radius spheres into a cylindrical region representing a fuel compact, setting each sphere to be filled with the TRISO universe.
#!/bin/env python
from argparse import ArgumentParser
import math
import numpy as np
import matplotlib.pyplot as plt
import openmc
import sys
import os
# Get common input parameters shared by other physics
script_dir = os.path.dirname(__file__)
sys.path.append(script_dir)
import common_input as specs
import materials as mats
def coolant_temp(t_in, t_out, l, z):
"""
THIS IS ONLY USED FOR SETTING AN INITIAL CONDITION IN OPENMC's XML FILES -
the coolant temperature will be applied from MOOSE, we just set an initial
value here in case you want to run these files in standalone mode (i.e. with
the "openmc" executable).
Computes the coolant temperature based on an expected cosine power distribution
for a specified temperature rise. The total core temperature rise is governed
by energy conservation as dT = Q / m / Cp, where dT is the total core temperature
rise, Q is the total core power, m is the mass flowrate, and Cp is the fluid
isobaric specific heat. If you neglect axial heat conduction and assume steady
state, then the temperature rise in a layer of fluid i can be related to the
ratio of the power in that layer to the total power,
dT_i / dT = Q_i / Q. We assume here a sinusoidal power distribution to get
a reasonable estimate of an initial coolant temperature distribution.
Parameters
----------
t_in : float
Inlet temperature of the channel
t_out : float
Outlet temperature of the channel
l : float
Length of the channel
z : float or 1-D numpy.array
Axial position where the temperature will be computed
Returns
-------
float or 1-D numpy array of float depending on z
"""
dT = t_out - t_in
Q = 2 * l / math.pi
distance_from_inlet = specs.unit_cell_height - z
Qi = (l - l * np.cos(math.pi * distance_from_inlet / l)) / math.pi
t = t_in + Qi / Q * dT
return t
def coolant_density(t):
"""
THIS IS ONLY USED FOR SETTING AN INITIAL CONDITION IN OPENMC's XML FILES -
the coolant density will be applied from MOOSE, we just set an initial
value here in case you want to run these files in standalone mode (i.e. with
the "openmc" executable).
Computes the helium density (kg/m3) from temperature assuming a fixed operating pressure.
Parameters
----------
t : float
Fluid temperature
Returns
_______
float or 1-D numpy array of float depending on t
"""
p_in_bar = specs.outlet_P * 1.0e-5
return 48.14 * p_in_bar / (t + 0.4446 * p_in_bar / math.pow(t, 0.2))
# -------------- Unit Conversions: OpenMC requires cm -----------
m = 100.0
# -------------------------------------------
### RADIANT UNIT CELL SPECS (INFERRED FROM REPORTS) ###
unit_cell_mdot = specs.mdot / (specs.n_bundles * specs.n_coolant_channels_per_block)
unit_cell_power = specs.power / (specs.n_bundles * specs.n_coolant_channels_per_block) * (specs.unit_cell_height / specs.height)
# estimate the outlet temperature using bulk energy conservation for steady state
coolant_outlet_temp = unit_cell_power / unit_cell_mdot / specs.fluid_Cp + specs.inlet_T
# geometry
coolant_channel_diam = specs.channel_diameter * m
reactor_bottom = 0.0
reactor_height = specs.unit_cell_height * m
reactor_top = reactor_bottom + reactor_height
### ARBITRARILY DETERMINED PARAMETERS ###
cell_pitch = specs.fuel_to_coolant_distance * m
fuel_channel_diam = specs.compact_diameter * m
hex_orientation = 'x'
def unit_cell(n_ax_zones, n_inactive, n_active):
axial_section_height = reactor_height / n_ax_zones
# superimposed search lattice
triso_lattice_shape = (4, 4, int(axial_section_height))
lattice_orientation = 'x'
cell_edge_length = cell_pitch
model = openmc.model.Model()
### Geometry ###
# TRISO particle
radius_pyc_outer = specs.oPyC_radius * m
s_fuel = openmc.Sphere(r=specs.kernel_radius*m)
s_c_buffer = openmc.Sphere(r=specs.buffer_radius*m)
s_pyc_inner = openmc.Sphere(r=specs.iPyC_radius*m)
s_sic = openmc.Sphere(r=specs.SiC_radius*m)
s_pyc_outer = openmc.Sphere(r=radius_pyc_outer)
c_triso_fuel = openmc.Cell(name='c_triso_fuel' , fill=mats.m_fuel, region=-s_fuel)
c_triso_c_buffer = openmc.Cell(name='c_triso_c_buffer' , fill=mats.m_graphite_c_buffer, region=+s_fuel & -s_c_buffer)
c_triso_pyc_inner = openmc.Cell(name='c_triso_pyc_inner', fill=mats.m_graphite_pyc, region=+s_c_buffer & -s_pyc_inner)
c_triso_sic = openmc.Cell(name='c_triso_sic' , fill=mats.m_sic, region=+s_pyc_inner & -s_sic)
c_triso_pyc_outer = openmc.Cell(name='c_triso_pyc_outer', fill=mats.m_graphite_pyc, region=+s_sic & -s_pyc_outer)
c_triso_matrix = openmc.Cell(name='c_triso_matrix' , fill=mats.m_graphite_matrix, region=+s_pyc_outer)
u_triso = openmc.Universe(cells=[c_triso_fuel, c_triso_c_buffer, c_triso_pyc_inner, c_triso_sic, c_triso_pyc_outer, c_triso_matrix])
# Channel surfaces
fuel_cyl = openmc.ZCylinder(r=0.5 * fuel_channel_diam)
coolant_cyl = openmc.ZCylinder(r=0.5 * coolant_channel_diam)
# create a TRISO lattice for one axial section (to be used in the rest of the axial zones)
# center the TRISO region on the origin so it fills lattice cells appropriately
min_z = openmc.ZPlane(z0=-0.5 * axial_section_height)
max_z = openmc.ZPlane(z0=0.5 * axial_section_height)
# region in which TRISOs are generated
r_triso = -fuel_cyl & +min_z & -max_z
rand_spheres = openmc.model.pack_spheres(radius=radius_pyc_outer, region=r_triso, pf=specs.triso_pf, seed=1.0)
random_trisos = [openmc.model.TRISO(radius_pyc_outer, u_triso, i) for i in rand_spheres]
llc, urc = r_triso.bounding_box
pitch = (urc - llc) / triso_lattice_shape
# insert TRISOs into a lattice to accelerate point location queries
triso_lattice = openmc.model.create_triso_lattice(random_trisos, llc, pitch, triso_lattice_shape, mats.m_graphite_matrix)
# create a hexagonal lattice for the coolant and fuel channels
fuel_univ = openmc.Universe(cells=[openmc.Cell(region=-fuel_cyl, fill=triso_lattice),
openmc.Cell(region=+fuel_cyl, fill=mats.m_graphite_matrix)])
# extract the coolant cell and set temperatures based on the axial profile
coolant_cell = openmc.Cell(region=-coolant_cyl, fill=mats.m_coolant)
# set the coolant temperature on the cell to approximately match the expected
# temperature profile
axial_coords = np.linspace(reactor_bottom, reactor_top, n_ax_zones + 1)
lattice_univs = []
fuel_ch_cells = []
i = 0
for z_min, z_max in zip(axial_coords[0:-1], axial_coords[1:]):
# create a new coolant universe for each axial zone in the coolant channel;
# this generates a new material as well (we only need to do this for all
# cells except the first cell)
if (i == 0):
c_cell = coolant_cell
else:
c_cell = coolant_cell.clone()
i += 1
# use the middle of the axial section to compute the temperature and density
ax_pos = 0.5 * (z_min + z_max)
t = coolant_temp(specs.inlet_T, coolant_outlet_temp, reactor_height, ax_pos)
c_cell.temperature = t
c_cell.fill.set_density('kg/m3', coolant_density(t))
# set the solid cells and their temperatures
graphite_cell = openmc.Cell(region=+coolant_cyl, fill=mats.m_graphite_matrix)
fuel_ch_cell = openmc.Cell(region=-fuel_cyl, fill=triso_lattice)
fuel_ch_matrix_cell = openmc.Cell(region=+fuel_cyl, fill=mats.m_graphite_matrix)
graphite_cell.temperature = t
fuel_ch_cell.temperature = t
fuel_ch_matrix_cell.temperature = t
fuel_ch_cells.append(fuel_ch_cell)
fuel_u = openmc.Universe(cells=[fuel_ch_cell, fuel_ch_matrix_cell])
coolant_u = openmc.Universe(cells=[c_cell, graphite_cell])
lattice_univs.append([[fuel_u] * 6, [coolant_u]])
# create a hexagonal lattice used in each axial zone to represent the cell
hex_lattice = openmc.HexLattice(name="Unit cell lattice")
hex_lattice.orientation = lattice_orientation
hex_lattice.center = (0.0, 0.0, 0.5 * (reactor_bottom + reactor_top))
hex_lattice.pitch = (cell_pitch, axial_section_height)
hex_lattice.universes = lattice_univs
graphite_outer_cell = openmc.Cell(fill=mats.m_graphite_matrix)
graphite_outer_cell.temperature = t
inf_graphite_univ = openmc.Universe(cells=[graphite_outer_cell])
hex_lattice.outer = inf_graphite_univ
# hexagonal bounding cell
hex = openmc.model.HexagonalPrism(cell_edge_length, hex_orientation, boundary_type='periodic')
hex_cell_vol = 6.0 * (math.sqrt(3) / 4.0) * cell_edge_length**2 * reactor_height
# create additional axial regions
axial_planes = [openmc.ZPlane(z0=coord) for coord in axial_coords]
# axial planes
min_z = axial_planes[0]
min_z.boundary_type = 'vacuum'
max_z = axial_planes[-1]
max_z.boundary_type = 'vacuum'
# fill the unit cell with the hex lattice
hex_cell = openmc.Cell(region=-hex & +min_z & -max_z, fill=hex_lattice)
model.geometry = openmc.Geometry([hex_cell])
### Settings ###
settings = openmc.Settings()
settings.particles = 150000
settings.inactive = n_inactive
settings.batches = settings.inactive + n_active
# the only reason we use 'nearest' here is to be sure we have a robust test for CI;
# otherwise, 1e-16 differences in temperature (due to numerical roundoff when using
# different MPI ranks) do change the tracking do to the stochastic interpolation
settings.temperature['method'] = 'nearest'
settings.temperature['range'] = (294.0, 1500.0)
settings.temperature['tolerance'] = 200.0
hexagon_half_flat = math.sqrt(3.0) / 2.0 * cell_edge_length
lower_left = (-cell_edge_length, -hexagon_half_flat, reactor_bottom)
upper_right = (cell_edge_length, hexagon_half_flat, reactor_top)
source_dist = openmc.stats.Box(lower_left, upper_right)
source = openmc.IndependentSource(space=source_dist)
settings.source = source
model.settings = settings
m_colors = {}
m_colors[mats.m_coolant] = 'royalblue'
m_colors[mats.m_fuel] = 'red'
m_colors[mats.m_graphite_c_buffer] = 'black'
m_colors[mats.m_graphite_pyc] = 'orange'
m_colors[mats.m_sic] = 'yellow'
m_colors[mats.m_graphite_matrix] = 'silver'
plot1 = openmc.Plot()
plot1.filename = 'plot1'
plot1.width = (2 * cell_pitch, 4 * axial_section_height)
plot1.basis = 'xz'
plot1.origin = (0.0, 0.0, reactor_height/2.0)
plot1.pixels = (int(800 * 2 * cell_pitch), int(800 * 4 * axial_section_height))
plot1.color_by = 'cell'
plot2 = openmc.Plot()
plot2.filename = 'plot2'
plot2.width = (3 * cell_pitch, 3 * cell_pitch)
plot2.basis = 'xy'
plot2.origin = (0.0, 0.0, axial_section_height / 2.0)
plot2.pixels = (int(800 * cell_pitch), int(800 * cell_pitch))
plot2.color_by = 'material'
plot2.colors = m_colors
plot3 = openmc.Plot()
plot3.filename = 'plot3'
plot3.width = plot2.width
plot3.basis = plot2.basis
plot3.origin = plot2.origin
plot3.pixels = plot2.pixels
plot3.color_by = 'cell'
model.plots = openmc.Plots([plot1, plot2, plot3])
return model
def main():
ap = ArgumentParser()
ap.add_argument('-n', dest='n_axial', type=int, default=50,
help='Number of axial cell divisions')
ap.add_argument('-i', dest='n_inactive', type=int, default=20,
help='Number of inactive cycles')
ap.add_argument('-a', dest='n_active', type=int, default=45,
help='Number of active cycles')
args = ap.parse_args()
model = unit_cell(args.n_axial, args.n_inactive, args.n_active)
model.export_to_xml()
if __name__ == "__main__":
main()
Finally, we loop over axial layers and create unique cells for each of the six compacts, the graphite block, and the coolant. Recall that we need unique cells in order for each region to obtain a a unique temperature from MOOSE. The level on which we will apply feedback from MOOSE is set to 1 because each layer is a component in a lattice nested once with respect to the highest level. To accelerate the particle tracking, we:
Repeat the same TRISO universe in each axial layer and within each compact
Superimpose a Cartesian search lattice in the fuel channel regions.
The OpenMC geometry, colored by cell ID, is shown in Figure 3. The lateral faces of the unit cell are periodic, while the top and bottom boundaries are vacuum. The Cartesian search lattice in the fuel compact regions is also visible.
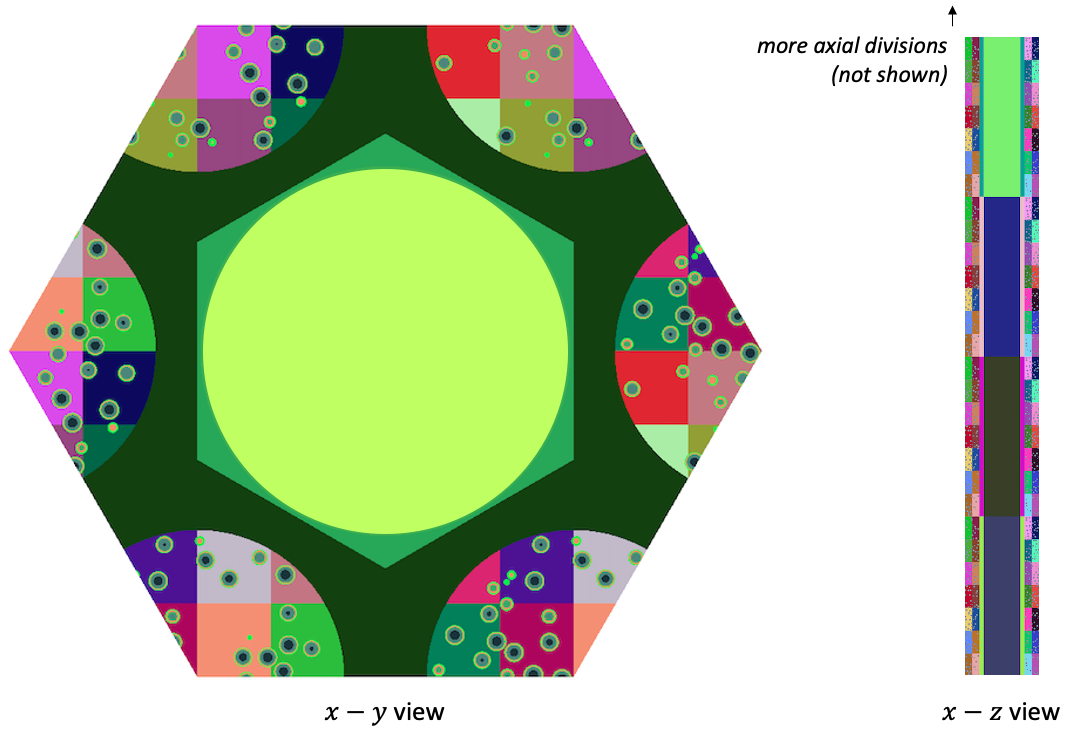
Figure 3: OpenMC model, colored by cell ID
For the "single-stack" MultiApp hierarchy, OpenMC runs first, so the initial temperature is set to uniform in the radial direction and given by a linear variation between the inlet and outlet fluid temperatures. The fluid density is then set using the ideal gas Equation of State (EOS) with pressure taken as the fixed outlet of 7.1 MPa given the temperature, i.e. . For the "tree" MultiApp hierarchy, OpenMC instead runs after the MOOSE heat transfer module, but before THM. For this structure, initial conditions are only required for fluid temperature and density, which are taken as the same initial conditions as for the "single-stack" case.
To create the XML files required to run OpenMC, run the script:
python unit_cell.py
You can also use the XML files checked in to the tutorials/gas_compact_multiphysics directory.
Heat Conduction Model
The MOOSE heat transfer module is used to solve for energy conservation in the solid. The solid mesh is shown in Figure 4; the only sideset defined in the domain is the coolant channel surface. The solid geometry uses a length unit of meters.
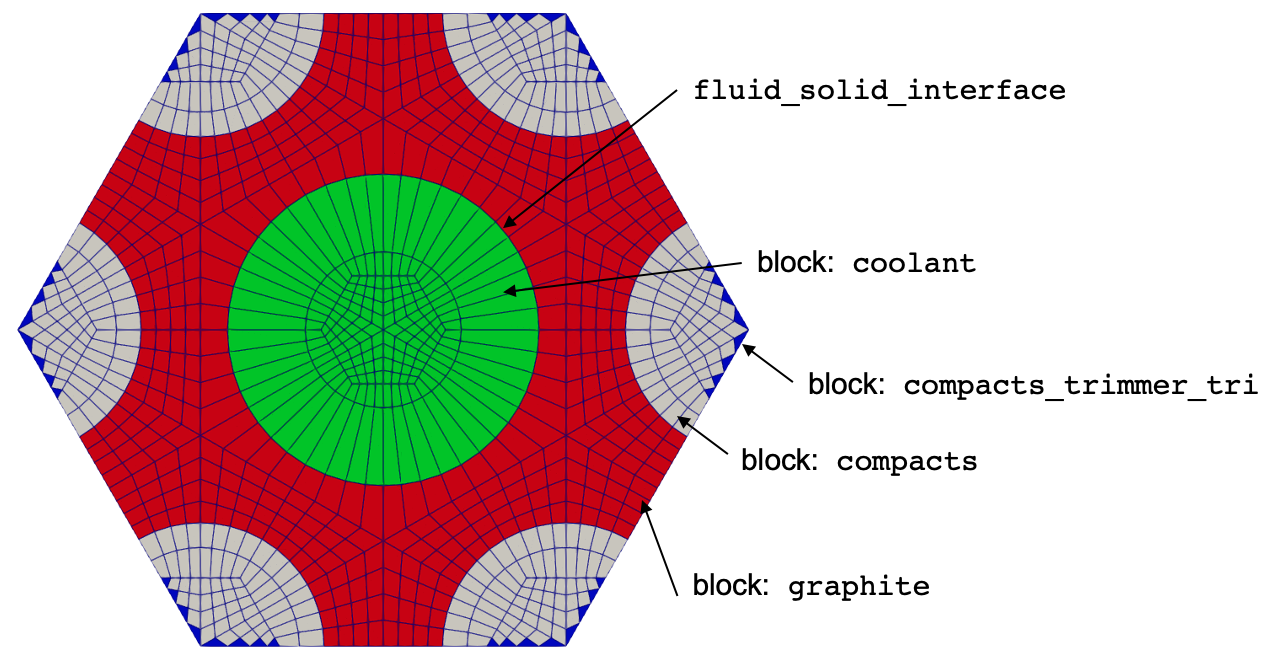
Figure 4: Mesh for the solid heat conduction model
This mesh is generated using MOOSE mesh generators in the solid_mesh.i file.
[Mesh]
[fuel_pin]
type = PolygonConcentricCircleMeshGenerator
num_sides = 6
polygon_size = '${fparse fuel_to_coolant_distance / 2.0}'
ring_radii = '${fparse 0.8 * compact_diameter / 2.0} ${fparse compact_diameter / 2.0}'
ring_intervals = '1 1'
num_sectors_per_side = '${ns} ${ns} ${ns} ${ns} ${ns} ${ns}'
ring_block_ids = '2 2'
ring_block_names = 'compacts compacts'
background_block_names = 'graphite'
background_intervals = 4
[]
[coolant_pin]
type = PolygonConcentricCircleMeshGenerator
num_sides = 6
polygon_size = '${fparse fuel_to_coolant_distance / 2.0}'
ring_radii = '${fparse channel_diameter / 2.0}'
ring_intervals = '2'
num_sectors_per_side = '${ns} ${ns} ${ns} ${ns} ${ns} ${ns}'
ring_block_ids = '101 101'
ring_block_names = 'coolant coolant'
background_block_names = 'graphite'
interface_boundary_id_shift = 100
background_intervals = 3
[]
[bundle]
type = PatternedHexMeshGenerator
inputs = 'fuel_pin coolant_pin'
hexagon_size = '${fparse 2.0 * fuel_to_coolant_distance}'
pattern = '0 0;
0 1 0;
0 0'
[]
[trim]
type = HexagonMeshTrimmer
input = bundle
trim_peripheral_region = '1 1 1 1 1 1'
peripheral_trimming_section_boundary = peripheral_section
[]
[rotate]
type = TransformGenerator
input = trim
transform = rotate
vector_value = '30.0 0.0 0.0'
[]
[extrude]
type = AdvancedExtruderGenerator
input = rotate
heights = ${height}
num_layers = ${n_layers}
direction = '0 0 1'
[]
[fluid_solid_interface]
type = SideSetsBetweenSubdomainsGenerator
input = extrude
primary_block = 'graphite'
paired_block = 'coolant'
new_boundary = 'fluid_solid_interface'
[]
[]
We first create a full 7-pin bundle, and then apply a trimming operation to split the compacts. Because MOOSE does not support multiple element types (e.g. tets, hexes) on the same block ID, the trimmer automatically creates an additional block (compacts_trimmer_tri) to represent the triangular prism elements formed in the compacts. Note that within this mesh, we include the fluid region - for the "single stack" MultiApp hierarchy, we will need somewhere for NekRS to write the fluid temperature solution. So, while this block does not participate in the solid solve, we include it in the mesh just for data transfers. You can generate this mesh by running
cardinal-opt -i solid_mesh.i --mesh-only
which will create the mesh, named solid_mesh_in.e.
On the coolant channel surface, a Dirichlet temperature is provided by NekRS/THM. All other boundaries are insulated. The volumetric power density is provided by OpenMC, with normalization to ensure the total specified power. When using the "single stack" hierarchy, MOOSE runs after OpenMC but before NekRS, and an initial condition is only required for the wall temperature, which is set to a linear variation from inlet to outlet fluid temperature. When using the "tree" hierarchy, MOOSE runs first, in which case the initial wall temperature is taken as the same linear variation, while the power is taken as uniform.
NekRS Model
NekRS is used to solve the incompressible k-tau RANS model. The inlet mass flowrate is 0.0905 kg/s; with the channel diameter of 1.6 cm and material properties of helium, this results in a Reynolds number of 223214 and a Prandtl number of 0.655. This highly-turbulent flow results in extremely thin momentum and thermal boundary layers on the no-slip surfaces forming the periphery of the coolant channel. In order to resolve the near-wall behavior with a wall-resolved model, an extremely fine mesh is required in the NekRS simulation. To accelerate the overall coupled solve that is of interest in this tutorial, the NekRS model is split into a series of calculations:
We first run a partial-height, periodic flow-only case to obtain converged , , and distributions.
Then, we extrapolate the and to the full-height case.
We use the converged, full-height and distributions to transport a temperature passive scalar in a Conjugate Heat Transfer (CHT) calculation with MOOSE.
Finally, we use the converged CHT case as an initial condition for the multiphysics simulation with OpenMC and MOOSE feedback.
Steps 1-3 were performed in an earlier tutorial - for brevity, we skip repeating the discussion of steps 1-3.
For the multiphysics case, we will load the restart file produced from step 3, compute from the loaded solutions for and , and then transport temperature with coupling to MOOSE heat conduction and OpenMC particle transport. Let's now describe the NekRS input files needed for the passive scalar solve:
ranstube.re2: NekRS meshranstube.par: High-level settings for the solver, boundary condition mappings to sidesets, and the equations to solveranstube.udf: User-defined C++ functions for on-line postprocessing and model setupranstube.oudf: User-defined Open Concurrent Compute Abstraction (OCCA) kernels for boundary conditions and source terms
A detailed description of all of the available parameters, settings, and use cases for these input files is available on the NekRS documentation website. Because the purpose of this analysis is to demonstrate Cardinal's capabilities, only the aspects of NekRS required to understand the present case will be covered. First, the NekRS mesh is shown in Figure 5. Boundary 1 is the inlet, boundary 2 is the outlet, and boundary 3 is the wall. The same mesh was used for the periodic flow solve, except with a shorter height.
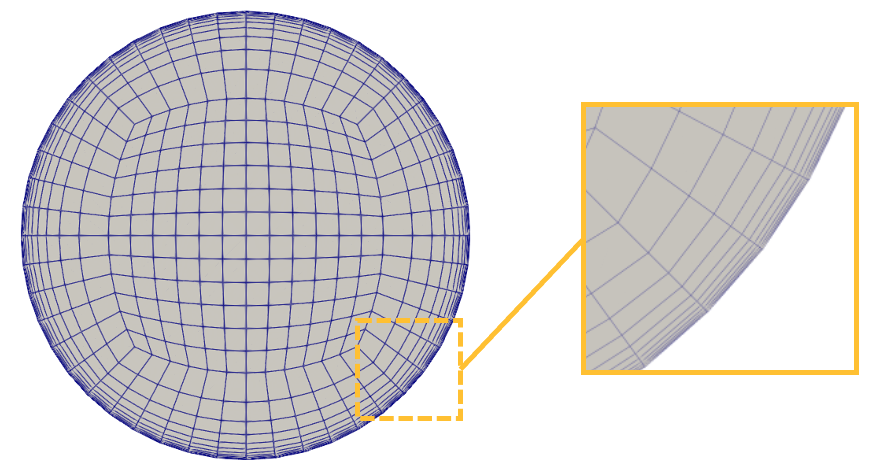
Figure 5: Mesh for the NekRS RANS model
Next, the .par file contains problem setup information. This input sets up a nondimensional passive scalar solution, loading , , , and from a restart file. We "freeze" the flow by setting solver = none in the [VELOCITY], [SCALAR01] ( passive scalar), and [SCALAR02] ( passive scalar) blocks. In the nondimensional formulation, the "viscosity" becomes , where is the Reynolds number, while the "thermal conductivity" becomes , where is the Peclet number. These nondimensional numbers are used to set various diffusion coefficients in the governing equations with syntax like -223214, which is equivalent in NekRS syntax to . The only equation that NekRS will solve is for temperature.
# Model of a turbulent channel flow.
#
# L_ref = 0.016 m coolant channel diameter
# T_ref = 598 K coolant inlet temperature
# dT_ref = 82.89 K coolant nominal temperature rise in the unit cell
# U_ref = 81.089 coolant inlet velocity
# length = 1.6 m coolant channel flow length
#
# rho_0 = 5.5508 kg/m3 coolant density
# mu_0 = 3.22639e-5 Pa-s coolant dynamic viscosity
# Cp_0 = 5189 J/kg/K coolant isobaric heat capacity
# k_0 = 0.2556 W/m/K coolant thermal conductivity
#
# Re = 223214
# Pr = 0.655
# Pe = 146205
[GENERAL]
startFrom = converged_cht.fld
polynomialOrder = 7
dt = 6e-3
timeStepper = BDF2
# end the simulation at specified number of time steps
stopAt = numSteps
numSteps = 1000
# write an output file every specified time steps
writeControl = steps
writeInterval = 1000
[PROBLEMTYPE]
stressFormulation = true
[PRESSURE]
residualTol = 1e-04
[VELOCITY]
solver = none
viscosity = -223214
density = 1.0
boundaryTypeMap = v, o, W
residualTol = 1e-06
[TEMPERATURE]
rhoCp = 1.0
conductivity = -146205
boundaryTypeMap = t, o, f
residualTol = 1e-06
[SCALAR01] # k
solver = none
boundaryTypeMap = t, I, o
residualTol = 1e-06
rho = 1.0
diffusivity = -223214
[SCALAR02] # tau
solver = none
boundaryTypeMap = t, I, o
residualTol = 1e-06
rho = 1.0
diffusivity = -223214
Next, the .udf file is used to setup initial conditions and define how should be computed based on and the restart values of and . In turbulent_props, a user-defined function, we use from the input file in combination with the and (read from the restart file later in the .udf file) to adjust the total diffusion coefficient on temperature to according to the turbulent Prandtl number definition. This adjustment must happen on device, in a new GPU kernel we name scalarScaledAddKernel. This kernel will be defined in the .oudf file; we instruct the JIT compilation to compile this new kernel by calling udfBuildKernel.
Then, in UDF_Setup we store the value of computed in the restart file.
#include <math.h>
#include "udf.hpp"
occa::memory o_mu_t_from_restart;
#define length 100.0 // non-dimensional channel length
#define Pr_T 0.91 // turbulent Prandtl number
static occa::kernel scalarScaledAddKernel;
void turbulent_props(nrs_t *nrs, double time, occa::memory o_U, occa::memory o_S,
occa::memory o_UProp, occa::memory o_SProp)
{
// fetch the laminar thermal conductivity and specify the desired turbulent Pr
dfloat k_laminar;
platform->options.getArgs("SCALAR00 DIFFUSIVITY", k_laminar);
// o_diff is the turbulent conductivity for all passive scalars, so we grab the first
// slice, since temperature is the first passive scalar
occa::memory o_mu = nrs->cds->o_diff + 0 * nrs->cds->fieldOffset[0] * sizeof(dfloat);
scalarScaledAddKernel(0, nrs->cds->mesh[0]->Nlocal, k_laminar, 1.0 / Pr_T,
o_mu_t_from_restart /* turbulent viscosity */, o_mu /* laminar viscosity */);
}
void UDF_LoadKernels(occa::properties & kernelInfo)
{
scalarScaledAddKernel = oudfBuildKernel(kernelInfo, "scalarScaledAdd");
}
void UDF_Setup(nrs_t *nrs)
{
mesh_t *mesh = nrs->cds->mesh[0];
int n_gll_points = mesh->Np * mesh->Nelements;
// allocate space for the k and tau that we will read from the file
dfloat * mu_t = (dfloat *) calloc(n_gll_points, sizeof(dfloat));
for (int n = 0; n < n_gll_points; ++n)
{
// fetch the restart value of mu_T, which is equal to k * tau, the second and third
// passive scalars
mu_t[n] = nrs->cds->S[n + 1 * nrs->cds->fieldOffset[0]] *
nrs->cds->S[n + 2 * nrs->cds->fieldOffset[0]];
}
o_mu_t_from_restart = platform->device.malloc(n_gll_points * sizeof(dfloat), mu_t);
udf.properties = &turbulent_props;
}
void UDF_ExecuteStep(nrs_t * nrs, double time, int tstep)
{
}
In the .oudf file, we define boundary conditions for temperature and also the form of the scalarScaledAdd kernel that we use to compute . The inlet boundary is set to a temperature of 0 (a dimensional temperature of ), while the fluid-solid interface will receive a heat flux from MOOSE.
@kernel void scalarScaledAdd(const dlong offset, const dlong N,
const dfloat a,
const dfloat b,
@restrict const dfloat* X,
@restrict dfloat* Y)
{
for (dlong n = 0; n < N; ++n; @tile(256,@outer,@inner))
if (n < N)
Y[n] = a + b * X[n + offset];
}
// Boundary conditions are only needed for temperature, since the solves of pressure,
// velocity, k, and tau are all frozen
void scalarDirichletConditions(bcData *bc)
{
// inlet temperature
bc->s = 0.0;
}
void scalarNeumannConditions(bcData *bc)
{
// wall temperature
// note: when running with Cardinal, Cardinal will allocate the usrwrk
// array. If running with NekRS standalone (e.g. nrsmpi), you need to
// replace the usrwrk with some other value or allocate it youself from
// the udf and populate it with values.
bc->flux = bc->usrwrk[bc->idM];
}
For this tutorial, NekRS runs last in the "single-stack" MultiApp hierarchy, so no initial conditions are required aside from the , , and taken from the converged_cht.fld restart file on Box.
THM Model
THM is used to solve the 1-D area-averaged Navier-Stokes equations. The THM mesh contains 150 elements; the mesh is constucted automatically within THM. The fluid geometry uses a length unit of meters. The heat flux imposed in the THM elements is obtained by area averaging the heat flux from the heat conduction model in 150 layers along the fluid-solid interface. For the reverse transfer, the wall temperature sent to MOOSE heat conduction is set to a uniform value along the fluid-solid interface according to a nearest-node mapping to the THM elements.
For this tutorial, THM runs last in the "tree" MultiApp hierarchy; because THM solves time-dependent equations, initial conditions are only required for the solution variables for which THM solves - pressure, fluid temperature, and velocity, all of which are set to uniform conditions.
Multiphysics Coupling
In this section, OpenMC, NekRS/THM, and MOOSE heat conduction are coupled for multiphysics modeling of the TRISO gas compact. Two separate simulations are performed here:
Coupling of OpenMC, NekRS, and MOOSE heat conduction in a "single-stack" MultiApp hierarchy
Coupling of OpenMC, THM, and MOOSE heat conduction in a "tree" MultiApp hierarchy
By individually describing the two setups, you will understand the customizability of the MultiApp system and the flexibility shared by all MOOSE applications for seamlessly exchanging tools of varying resolution for one another.
OpenMC-NekRS-MOOSE
In this section, we describe the coupling of OpenMC, NekRS, and MOOSE in the "single-stack" MultiApp hierarchy shown in Figure 2.
OpenMC Input Files
The neutronics physics is solved over the entire domain with OpenMC. The OpenMC wrapping used for the OpenMC-NekRS-MOOSE coupling is described in the openmc_nek.i input file. We begin by defining a number of constants and by setting up the mesh mirror on which OpenMC will receive temperature and density from THM-MOOSE, and on which OpenMC will write the fission heat source. Because the coupled applications use length units of meters, the mesh mirror must also be in units of meters. For simplicity, we just use the same mesh as generated with solid_mesh.i earlier, though this it not necessary.
# This input file runs coupled OpenMC Monte Carlo transport, MOOSE heat
# conduction, and NekRS fluid flow and heat transfer.
# This input should be run with:
#
# cardinal-opt -i common_input.i openmc_nek.i
num_layers_for_THM = 150
density_blocks = 'coolant'
temperature_blocks = 'graphite compacts compacts_trimmer_tri'
fuel_blocks = 'compacts compacts_trimmer_tri'
unit_cell_power = ${fparse power / (n_bundles * n_coolant_channels_per_block) * unit_cell_height / height}
U_ref = ${fparse mdot / (n_bundles * n_coolant_channels_per_block) / fluid_density / (pi * channel_diameter * channel_diameter / 4.0)}
t0 = ${fparse channel_diameter / U_ref}
nek_dt = 6e-3
N = 1000
[Mesh]
[solid]
type = FileMeshGenerator
file = solid_mesh_in.e
[]
[]
Next, we define a number of auxiliary variables to query the OpenMC solution and set up multiphysics coupling. We add cell_temperature and cell_density in order to read the cell temperatures and densities directly from OpenMC in order to visualize the temperatures and densities ultimately applied to OpenMC's cells. In order to compute density using the ideal gas EOS given a temperature and a fixed pressure, we use a FluidDensityAux to set density.
[AuxVariables]
[cell_temperature]
family = MONOMIAL
order = CONSTANT
[]
[cell_density]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[cell_temperature]
type = CellTemperatureAux
variable = cell_temperature
[]
[cell_density]
type = CellDensityAux
variable = cell_density
[]
[density]
type = FluidDensityAux
variable = density
p = ${outlet_P}
T = nek_temp
fp = helium
execute_on = 'timestep_begin'
[]
[]
[FluidProperties]
[helium]
type = IdealGasFluidProperties
molar_mass = 4e-3
gamma = 1.668282 # should correspond to Cp = 5189 J/kg/K
k = 0.2556
mu = 3.22639e-5
[]
[]
Next, we define the necessary initial conditions using functions; all temperatures (nek_temp and solid_temp are to be discussed shortly) are set to a linear variation from the inlet to outlet fluid temperatures.
[ICs]
[temp]
type = FunctionIC
variable = nek_temp
function = temp_ic
[]
[solid_temp]
type = FunctionIC
variable = solid_temp
function = temp_ic
[]
[]
[Functions]
[temp_ic]
type = ParsedFunction
expression = '${inlet_T} + z / ${unit_cell_height} * ${unit_cell_power} / (${mdot} / ${n_bundles} / ${n_coolant_channels_per_block}) / ${fluid_Cp}'
[]
[]
The wrapping of OpenMC is specified in the [Problem] block and the addition of tallies is done in the [Tallies] block. Here, we indicate that we will provide both temperature and density feedback to OpenMC. In order to visualize the tally standard deviation, we output the fission tally standard deviation using the output parameter. The heat source from OpenMC will be relaxed using Robbins-Monro relaxation.
By default, OpenMC will try to read temperature from the temp variable. However, in this case we have multiple applications (NekRS/THM for the fluids, MOOSE for the solids) which want to send temperatures into OpenMC. To be sure one data transfer does not overwrite the second, we need to tell OpenMC the names of the variables to read temperature from. Cardinal contains convenient syntax to automatically set up the necessary receiver variables for temperature, by using the temperature_variables and temperature_blocks parameters.
Finally, a number of "triggers" are used to automatically terminate OpenMC's active batches once reaching desired uncertainties in and the fission tally. The number of batches here is terminated once both of the following are satisfied:
Standard deviation in is less than 75 pcm
Maximum fission tally relative error is less than 1%
These criteria are checked every batch_interval, up to a maximum number of batches.
[Problem]
type = OpenMCCellAverageProblem
power = ${unit_cell_power}
scaling = 100.0
density_blocks = ${density_blocks}
cell_level = 1
relaxation = robbins_monro
temperature_variables = 'solid_temp; nek_temp'
temperature_blocks = '${temperature_blocks}; ${density_blocks}'
k_trigger = std_dev
k_trigger_threshold = 7.5e-4
batches = 40
max_batches = 100
batch_interval = 5
[Tallies]
[heat_source]
type = CellTally
blocks = ${fuel_blocks}
name = heat_source
check_equal_mapped_tally_volumes = true
trigger = rel_err
trigger_threshold = 1e-2
output = 'unrelaxed_tally_std_dev'
[]
[]
[]
Next, we define a transient executioner - while OpenMC is technically solving a steady -eigenvalue problem, using a time-dependent executioner with the notion of a "time step" will allow us to control the frequency with which OpenMC sends data to/from it's sub-app (MOOSE heat conduction). Here, we set the time step to be 1000 times the NekRS fluid time step. We will terminate the solution once reaching the specified steady_state_tolerance, which by setting check_aux = true will terminate the entire solution once reaching less than 1% change in all auxiliary variables in the OpenMC input file (which includes temperatures and power).
[Executioner]
type = Transient
dt = '${fparse N * nek_dt * t0}'
# This is somewhat loose, and you should use a tighter tolerance for production runs;
# we use 1e-2 to obtain a faster tutorial
steady_state_detection = true
check_aux = true
steady_state_tolerance = 1e-2
[]
Next, we define the MOOSE heat conduction sub-application and data transfers to/from that application. Most important to note is that while the MOOSE heat transfer module does not itself compute fluid temperature, we see a transfer getting the fluid temperature that has been transferred to the MOOSE heat transfer module by the doubly-nested NekRS sub-application.
[MultiApps]
[bison]
type = TransientMultiApp
input_files = 'solid_nek.i'
execute_on = timestep_end
sub_cycling = true
[]
[]
[Transfers]
[solid_temp_to_openmc]
type = MultiAppGeometricInterpolationTransfer
source_variable = T
variable = solid_temp
from_multi_app = bison
[]
[source_to_bison]
type = MultiAppGeneralFieldShapeEvaluationTransfer
source_variable = heat_source
variable = power
to_multi_app = bison
from_postprocessors_to_be_preserved = heat_source
to_postprocessors_to_be_preserved = power
[]
[temp_from_nek]
type = MultiAppGeneralFieldShapeEvaluationTransfer
source_variable = nek_bulk_temp
from_multi_app = bison
variable = nek_temp
[]
[]
Next, we define several postprocessors for querying the solution. The heat_source postprocessor will be used to ensure conservation of power when sent to the MOOSE heat conduction application. All other postprocessors are used for general solution monitoring purposes.
[Postprocessors]
[heat_source]
type = ElementIntegralVariablePostprocessor
variable = heat_source
execute_on = 'transfer initial timestep_end'
[]
[max_tally_err]
type = TallyRelativeError
value_type = max
[]
[k]
type = KEigenvalue
[]
[k_std_dev]
type = KStandardDeviation
[]
[min_power]
type = ElementExtremeValue
variable = heat_source
value_type = min
block = ${fuel_blocks}
[]
[max_power]
type = ElementExtremeValue
variable = heat_source
value_type = max
block = ${fuel_blocks}
[]
[]
For postprocessing, we also compute the average power distribution in a number of layers using a LayeredAverage and output to CSV using a SpatialUserObjectVectorPostprocessor, in combination with a CSV output.
[UserObjects]
[average_power_axial]
type = LayeredAverage
variable = heat_source
direction = z
num_layers = ${num_layers_for_plots}
block = ${fuel_blocks}
[]
[]
[VectorPostprocessors]
[power_avg]
type = SpatialUserObjectVectorPostprocessor
userobject = average_power_axial
[]
[]
[Outputs]
[out]
type = Exodus
hide = 'solid_temp nek_temp'
[]
[csv]
type = CSV
file_base = 'csv_nek/openmc_nek'
[]
[]
Solid Input Files
The solid heat conduction physics is solved over the solid regions of the unit cell using the MOOSE heat transfer module. The input file for this portion of the physics is the solid_nek.i input. We begin by defining a number of constants and by setting up the mesh for solving heat conduction.
channel_diameter = 0.016 # diameter of the coolant channels (m)
n_bundles = 12 # number of bundles in the full core
n_coolant_channels_per_block = 108 # number of coolant channels per assembly
unit_cell_height = 1.6 # unit cell height - arbitrarily selected
kernel_radius = 214.85e-6 # fissile kernel outer radius (m)
buffer_radius = 314.85e-6 # buffer outer radius (m)
iPyC_radius = 354.85e-6 # inner PyC outer radius (m)
SiC_radius = 389.85e-6 # SiC outer radius (m)
oPyC_radius = 429.85e-6 # outer PyC outer radius (m)
buffer_k = 0.5 # buffer thermal conductivity (W/m/K)
PyC_k = 4.0 # PyC thermal conductivity (W/m/K)
SiC_k = 13.9 # SiC thermal conductivity (W/m/K)
kernel_k = 3.5 # fissil kernel thermal conductivity (W/m/K)
matrix_k = 15.0 # graphite matrix thermal conductivity (W/m/K)
inlet_T = 598.0 # inlet fluid temperature (K)
power = 200e6 # full core power (W)
mdot = 117.3 # fluid mass flowrate (kg/s)
num_layers_for_plots = 50 # number of layers to average fields over for plotting
height = 6.343 # height of the full core (m)
fluid_density = 5.5508 # fluid density (kg/m3)
fluid_Cp = 5189.0 # fluid isobaric specific heat (J/kg/K)
triso_pf = 0.15 # TRISO packing fraction (%)
density_blocks = 'coolant'
temperature_blocks = 'graphite compacts compacts_trimmer_tri'
fuel_blocks = 'compacts compacts_trimmer_tri'
unit_cell_power = ${fparse power / (n_bundles * n_coolant_channels_per_block) * unit_cell_height / height}
unit_cell_mdot = ${fparse mdot / (n_bundles * n_coolant_channels_per_block)}
# compute the volume fraction of each TRISO layer in a TRISO particle
# for use in computing average thermophysical properties
kernel_fraction = ${fparse kernel_radius^3 / oPyC_radius^3}
buffer_fraction = ${fparse (buffer_radius^3 - kernel_radius^3) / oPyC_radius^3}
ipyc_fraction = ${fparse (iPyC_radius^3 - buffer_radius^3) / oPyC_radius^3}
sic_fraction = ${fparse (SiC_radius^3 - iPyC_radius^3) / oPyC_radius^3}
opyc_fraction = ${fparse (oPyC_radius^3 - SiC_radius^3) / oPyC_radius^3}
N = 50
U_ref = ${fparse mdot / (n_bundles * n_coolant_channels_per_block) / fluid_density / (pi * channel_diameter * channel_diameter / 4.0)}
t0 = ${fparse channel_diameter / U_ref}
nek_dt = 6e-3
[Mesh]
[solid]
type = FileMeshGenerator
file = solid_mesh_in.e
[]
[]
Because we have a block in the problem that we don't need to define any material properties on, we technically need to turn off a material coverage check, or else we're going to get an error from MOOSE. FEProblem is just the default problem, which we need to list in order to turn off the material coverage check.
[Problem]
type = FEProblem
material_coverage_check = false
[]
Next, we define the nonlinear variable that this application will solve for (T), the solid temperature. On the solid blocks, we solve the heat equation, but on the fluid blocks that exist exclusively for transferring data, we add a NullKernel to skip the solve in those regions. On the channel wall, the temperature from NekRS is applied as a Dirichlet condition.
[Variables]
[T]
initial_condition = ${inlet_T}
[]
[]
[Kernels]
[diffusion]
type = HeatConduction
variable = T
block = ${temperature_blocks}
[]
[source]
type = CoupledForce
variable = T
v = power
block = ${fuel_blocks}
[]
[null] # The value of T on the fluid blocks is meaningless
type = NullKernel
variable = T
block = ${density_blocks}
[]
[]
[BCs]
[pin_outer]
type = MatchedValueBC
variable = T
v = nek_temp
boundary = 'fluid_solid_interface'
[]
[]
[ICs]
[nek_temp]
type = FunctionIC
variable = nek_temp
function = axial_fluid_temp
[]
[]
Next, we define a number of functions to set the solid material properties and define an initial condition for the wall temperature. The solid material properties are then applied with a HeatConductionMaterial.
[ICs]
[nek_temp]
type = FunctionIC
variable = nek_temp
function = axial_fluid_temp
[]
[]
[Functions]
[k_graphite]
type = ParsedFunction
expression = '${matrix_k}'
[]
[k_TRISO]
type = ParsedFunction
expression = '${kernel_fraction} * ${kernel_k} + ${buffer_fraction} * ${buffer_k} + ${fparse ipyc_fraction + opyc_fraction} * ${PyC_k} + ${sic_fraction} * ${SiC_k}'
[]
[k_compacts]
type = ParsedFunction
expression = '${triso_pf} * k_TRISO + ${fparse 1.0 - triso_pf} * k_graphite'
symbol_names = 'k_TRISO k_graphite'
symbol_values = 'k_TRISO k_graphite'
[]
[axial_fluid_temp]
type = ParsedFunction
expression = '${inlet_T} + z / ${unit_cell_height} * ${unit_cell_power} / ${unit_cell_mdot} / ${fluid_Cp}'
[]
[]
[Materials]
[graphite]
type = HeatConductionMaterial
thermal_conductivity_temperature_function = k_graphite
temp = T
block = 'graphite'
[]
[compacts]
type = HeatConductionMaterial
thermal_conductivity_temperature_function = k_compacts
temp = T
block = ${fuel_blocks}
[]
[]
[AuxVariables]
[nek_temp]
block = ${density_blocks}
[]
[nek_bulk_temp]
block = ${density_blocks}
[]
[flux]
family = MONOMIAL
order = CONSTANT
[]
[power]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[flux]
type = DiffusionFluxAux
diffusion_variable = T
component = normal
diffusivity = thermal_conductivity
variable = flux
boundary = 'fluid_solid_interface'
[]
[]
Next, we define a number of auxiliary variables - power will receive the heat source from OpenMC, nek_temp will receive the wall temperature from NekRS, nek_bulk_temp will receive the volumetric fluid temperature from NekRS, and finally flux will be used to compute the wall heat flux to send to NekRS.
[AuxVariables]
[nek_temp]
block = ${density_blocks}
[]
[nek_bulk_temp]
block = ${density_blocks}
[]
[flux]
family = MONOMIAL
order = CONSTANT
[]
[power]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[flux]
type = DiffusionFluxAux
diffusion_variable = T
component = normal
diffusivity = thermal_conductivity
variable = flux
boundary = 'fluid_solid_interface'
[]
[]
We then add a NekRS sub-application and define the transfers to/from NekRS, including the transfer of fluid temperature from the NekRS volume to the dummy coolant blocks in the MOOSE solid model. Because the NekRS mesh mirror will be a volume mirror (in order to extract volumetric temperatures for the neutronics feedback), a significant cost savings can be obtained by using the "minimal transfer" feature of NekRSProblem (which requires sending a dummy Receiver postprocessor, here named synchronization_to_nek, to indicate when data is to be exchanged). For more information, please consult the documentation for NekRSProblem.
[MultiApps]
[nek]
type = TransientMultiApp
input_files = 'nek.i'
sub_cycling = true
execute_on = timestep_end
[]
[]
[Transfers]
[heat_flux_to_nek]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = flux
variable = avg_flux
from_boundaries = 'fluid_solid_interface'
to_boundaries = '3'
to_multi_app = nek
[]
[flux_integral_to_nek]
type = MultiAppPostprocessorTransfer
to_postprocessor = flux_integral
from_postprocessor = flux_integral
to_multi_app = nek
[]
[temperature_to_bison]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = temp
variable = nek_temp
from_boundaries = '3'
to_boundaries = 'fluid_solid_interface'
from_multi_app = nek
[]
[bulk_temperature_to_bison]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = temp
variable = nek_bulk_temp
from_multi_app = nek
[]
[synchronization_to_nek]
type = MultiAppPostprocessorTransfer
to_postprocessor = transfer_in
from_postprocessor = synchronization_to_nek
to_multi_app = nek
[]
[]
We add several postprocessors to facilitate the data transfers as well as to query the solution.
[Postprocessors]
[flux_integral]
# evaluate the total heat flux for normalization
type = SideDiffusiveFluxIntegral
diffusivity = thermal_conductivity
variable = T
boundary = 'fluid_solid_interface'
[]
[max_fuel_T]
type = ElementExtremeValue
variable = T
value_type = max
block = ${fuel_blocks}
[]
[max_block_T]
type = ElementExtremeValue
variable = T
value_type = max
block = 'graphite'
[]
[synchronization_to_nek]
type = Receiver
default = 1.0
[]
[power]
type = ElementIntegralVariablePostprocessor
variable = power
block = ${fuel_blocks}
execute_on = transfer
[]
[]
We add a transient executioner - again, even though the MOOSE heat conduction module in this tutorial solves steady equations, a transient executioner allows us to control the frequency with which MOOSE and NekRS iterate the CHT physics. Here, we use a time step that is 50 times bigger than the NekRS time step.
[Executioner]
type = Transient
dt = '${fparse N * nek_dt * t0}'
nl_abs_tol = 1e-5
nl_rel_tol = 1e-16
petsc_options_value = 'hypre boomeramg'
petsc_options_iname = '-pc_type -pc_hypre_type'
[]
The ability to use different data transfer "frequencies" is a key advantage of the "single-stack" MultiApp hierarchy. So far, we have shown that OpenMC will exchange data every 1000 time steps with MOOSE, but MOOSE exchanges data every 50 times steps with NekRS. In other words, for every update of the OpenMC fission distribution, we perform 20 sub-iterations of the CHT physics. Depending on the problem, begin able to iterate the thermal-fluid physics on a finer granularity than the neutronics feedback can be essential to obtaining a stable solution without an inordinately high number of Monte Carlo solves.
Finally, we add a number of LayeredAverage user objects to compute averages of the fuel and graphite temperatures in the axial direction, which are output to CSV using a SpatialUserObjectVectorPostprocessor, in combination with a CSV output.
[UserObjects]
[average_fuel_axial]
type = LayeredAverage
variable = T
direction = z
num_layers = ${num_layers_for_plots}
block = ${fuel_blocks}
[]
[average_block_axial]
type = LayeredAverage
variable = T
direction = z
num_layers = ${num_layers_for_plots}
block = 'graphite'
[]
[]
[VectorPostprocessors]
[fuel_axial_avg]
type = SpatialUserObjectVectorPostprocessor
userobject = average_fuel_axial
[]
[block_axial_avg]
type = SpatialUserObjectVectorPostprocessor
userobject = average_block_axial
[]
[]
[Outputs]
exodus = true
hide = 'synchronization_to_nek'
[csv]
file_base = 'csv/solid_nek'
type = CSV
[]
[]
Fluid Input Files
The fluid mass, momentum, and energy transport physics are solved using NekRS. The input file for this portion of the physics is the nek.i input. We begin by defining a number of constants and by setting up the NekRSMesh mesh mirror. Because we are coupling via boundary CHT to MOOSE, we set boundary = '3' so that we will be able to extract the boundary temperature from boundary 3 (the wall). We are also coupling via volumes to OpenMC higher in the MultiApp hierarchy. In order to extract volume representations of the fluid temperature, we also set volume = true.
# copy-pasta from common_input.i
channel_diameter = 0.016 # diameter of the coolant channels (m)
height = 6.343 # height of the full core (m)
inlet_T = 598.0 # inlet fluid temperature (K)
power = 200e6 # full core power (W)
mdot = 117.3 # fluid mass flowrate (kg/s)
fluid_density = 5.5508 # fluid density (kg/m3)
fluid_Cp = 5189.0 # fluid isobaric specific heat (J/kg/K)
n_bundles = 12 # number of bundles in the full core
n_coolant_channels_per_block = 108 # number of coolant channels per assembly
unit_cell_height = 1.6 # unit cell height - arbitrarily selected
[Mesh]
type = NekRSMesh
boundary = '3'
volume = true
scaling = ${channel_diameter}
[]
The bulk of the NekRS wrapping occurs in the [Problem] block with NekRSProblem. The NekRS input files are in non-dimensional form, whereas all other coupled applications use dimensional units. The various *_ref and *_0 parameters define the characteristic scales that were used to non-dimensionalize the NekRS input. In order to simplify the input file, we know a priori that OpenMC will not be sending a heat source to NekRS, so we set has_heat_source = false so that we don't need to add a dummy heat source kernel to the ranstube.oudf file. Finally, we indicate that we will be minimizing the data transfers in/out of NekRS unless new data is actually available from the MOOSE heat transfer module with the synchronization_interval = parent_app parameter.
[Problem]
type = NekRSProblem
casename = 'ranstube'
has_heat_source = false
n_usrwrk_slots = 2
nondimensional = true
U_ref = '${fparse mdot / (n_bundles * n_coolant_channels_per_block) / fluid_density / (pi * channel_diameter * channel_diameter / 4.0)}'
T_ref = ${inlet_T}
dT_ref = '${fparse power / mdot / fluid_Cp * unit_cell_height / height}'
L_ref = ${channel_diameter}
rho_0 = ${fluid_density}
Cp_0 = ${fluid_Cp}
synchronization_interval = parent_app
[]
Next, we will allow NekRS to select its own time step using the NekTimeStepper, combined with a transient executioner.
[Executioner]
type = Transient
[TimeStepper]
type = NekTimeStepper
[]
[]
We also add a number of postprocessors to query the Nek solution.
[Postprocessors]
[inlet_T]
type = NekSideAverage
field = temperature
boundary = '1'
[]
[outlet_T]
type = NekSideAverage
field = temperature
boundary = '2'
[]
[max_T]
type = NekVolumeExtremeValue
field = temperature
value_type = max
[]
[]
Finally, we define the output formats and hide the automatically-created flux_integral and transfer_in postprocessors from the screen (console) to have neater output.
[Outputs]
exodus = true
[screen]
type = Console
hide = 'flux_integral transfer_in'
[]
[csv]
file_base = 'csv/nek'
type = CSV
[]
[]
OpenMC-THM-MOOSE
In this section, we describe the coupling of OpenMC, THM, and MOOSE in the "tree" MultiApp hierarchy shown in Figure 2. For the most part, the OpenMC and MOOSE heat conduction input files only have small differences from those presented earlier for the OpenMC-NekRS-MOOSE coupling. Therefore, for the OpenMC and MOOSE heat conduction cases, we only point out the aspects that differ from the earlier presentation. Differences will exist in several areas:
Due to the use of the "tree" MultiApp hierarchy, different initial conditions are required because the applications execute in a different order
Due to the use of the "tree" MultiApp hierarhcy, the wall heat flux and wall temperature exchanged between MOOSE and THM will need to go "up a level" to their common parent application, while the thermal-fluid application can now directly send fluid temperature to OpenMC
THM requires a slightly different data transfer than NekRS due to its 1-D representation of the flow channels, which requires us to compute an average of the wall heat flux along the wall channel
OpenMC Input Files
The neutronics physics is solved over the entire domain with OpenMC. The OpenMC wrapping used for the OpenMC-THM-MOOSE coupling is described in the openm_thm.i input file. Relative to the OpenMC input files used for the OpenMC-NekRS-MOOSE coupling shown previously, we now need to add variables to hold the wall temperature, thm_temp_wall, that THM passes to the MOOSE heat transfer module, and the wall heat flux, flux, that the MOOSE heat transfer module passes to THM. Both of these are simply receiver variables that are written into by the two sub-applications (MOOSE heat conduction and THM).
[AuxVariables]
[cell_temperature]
family = MONOMIAL
order = CONSTANT
[]
[cell_density]
family = MONOMIAL
order = CONSTANT
[]
[thm_temp_wall]
family = MONOMIAL
order = CONSTANT
block = ${density_blocks}
[]
[flux]
[]
[q_wall]
[]
[]
Next, when using the "tree" MultiApp hierarchy, OpenMC runs after the MOOSE heat transfer module, but before THM. Therefore, initial conditions are required for the fluid temperature (for OpenMC) as well as for the fluid wall temperature (which will be sent to the MOOSE heat transfer module on the first time step). Because OpenMC sends its heat source to the MOOSE heat transfer module at the beginning of a time step, we also need to set an initial condition on the heat source.
[ICs]
[fluid_temp_wall]
type = FunctionIC
variable = thm_temp_wall
function = temp_ic
[]
[fluid_temp]
type = FunctionIC
variable = thm_temp
function = temp_ic
[]
[heat_source]
type = ConstantIC
variable = heat_source
block = ${fuel_blocks}
value = ${fparse unit_cell_power / (2.0 * pi * compact_diameter * compact_diameter / 4.0 * unit_cell_height)}
[]
[]
[Functions]
[temp_ic]
type = ParsedFunction
expression = '${inlet_T} + z / ${unit_cell_height} * ${unit_cell_power} / (${mdot} / ${n_bundles} / ${n_coolant_channels_per_block}) / ${fluid_Cp}'
[]
[]
The [Problem] block is identical to that shown earlier for the OpenMC-NekRS-MOOSE coupling. Next, we define the two sub-applications and the transfers. The transfers of wall heat flux and wall temperature between MOOSE and THM first pass up through OpenMC to one of the sub-applications, giving four additional transfers in the main application's input file than we saw for the "single-stack" hierarchy.
[MultiApps]
[bison]
type = TransientMultiApp
input_files = 'solid_thm.i'
execute_on = timestep_begin
[]
[thm]
type = FullSolveMultiApp
input_files = 'thm.i'
execute_on = timestep_end
max_procs_per_app = 1
bounding_box_padding = '0.1 0.1 0'
[]
[]
[Transfers]
[solid_temp_to_openmc]
type = MultiAppGeometricInterpolationTransfer
source_variable = T
variable = solid_temp
from_multi_app = bison
[]
[heat_flux_to_openmc]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = flux
variable = flux
from_multi_app = bison
from_boundaries = 'fluid_solid_interface'
to_boundaries = 'fluid_solid_interface'
from_postprocessors_to_be_preserved = flux_integral
to_postprocessors_to_be_preserved = flux_integral
[]
[source_to_bison]
type = MultiAppGeneralFieldShapeEvaluationTransfer
source_variable = heat_source
variable = power
to_multi_app = bison
from_postprocessors_to_be_preserved = heat_source
to_postprocessors_to_be_preserved = power
[]
[thm_temp_to_bison]
type = MultiAppGeometricInterpolationTransfer
source_variable = thm_temp_wall
variable = fluid_temp
to_multi_app = bison
[]
[q_wall_to_thm]
type = MultiAppGeneralFieldUserObjectTransfer
variable = q_wall
to_multi_app = thm
source_user_object = q_wall_avg
[]
[T_wall_from_thm]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = T_wall
from_multi_app = thm
variable = thm_temp_wall
[]
[T_bulk_from_thm]
type = MultiAppGeneralFieldNearestLocationTransfer
source_variable = T
from_multi_app = thm
variable = thm_temp
[]
[]
The advantage of the "tree" MultiApp hierarhcy is in the simpler solid input file that we will see in Solid Input Files , which will not need to have a dummy part of the mesh for the fluid region or any NullKernels.
Finally, because we are coupling to THM, we need to average the wall heat flux around the coolant channel into a number of layers to transfer from the 3-D MOOSE heat conduction model to the 1-D fluid flow model. Heat flux is averaged using a LayeredSideAverage.
[UserObjects]
[q_wall_avg]
type = LayeredSideAverage
boundary = fluid_solid_interface
variable = flux
# Note: make this to match the num_elems in the channel
direction = z
num_layers = ${num_layers_for_THM}
direction_min = 0.0
direction_max = ${unit_cell_height}
[]
[average_power_axial]
type = LayeredAverage
variable = heat_source
direction = z
num_layers = ${num_layers}
block = ${fuel_blocks}
[]
[]
All other aspects of the input file are the same as for the OpenMC-NekRS-MOOSE case.
Solid Input Files
The solid heat conduction input file is the solid_thm.i input. This input file is identical to the solid_nek.i input file for the OpenMC-NekRS-MOOSE case except for:
There are no MultiApps, and therefore no transfers, to a thermal-fluid code
There are no initial conditions in the input file, since OpenMC sends the MOOSE heat conduction file all necessary initial conditions for wall temperature and heat source
There is no need to explicitly turn off the material coverage check or add a NullKernel because there is not a dummy fluid block to receive fluid temperature from a sub-application
Because all of these differences are simply omissions, this concludes the discussion of the solid input file. For reference, the full file is below.
# copy-pasta from common_input.i
inlet_T = 598.0 # inlet fluid temperature (K)
buffer_k = 0.5 # buffer thermal conductivity (W/m/K)
PyC_k = 4.0 # PyC thermal conductivity (W/m/K)
SiC_k = 13.9 # SiC thermal conductivity (W/m/K)
kernel_k = 3.5 # fissil kernel thermal conductivity (W/m/K)
matrix_k = 15.0 # graphite matrix thermal conductivity (W/m/K)
num_layers_for_plots = 50 # number of layers to average fields over for plotting
triso_pf = 0.15 # TRISO packing fraction (%)
kernel_radius = 214.85e-6 # fissile kernel outer radius (m)
buffer_radius = 314.85e-6 # buffer outer radius (m)
iPyC_radius = 354.85e-6 # inner PyC outer radius (m)
SiC_radius = 389.85e-6 # SiC outer radius (m)
oPyC_radius = 429.85e-6 # outer PyC outer radius (m)
# compute the volume fraction of each TRISO layer in a TRISO particle
# for use in computing average thermophysical properties
kernel_fraction = ${fparse kernel_radius^3 / oPyC_radius^3}
buffer_fraction = ${fparse (buffer_radius^3 - kernel_radius^3) / oPyC_radius^3}
ipyc_fraction = ${fparse (iPyC_radius^3 - buffer_radius^3) / oPyC_radius^3}
sic_fraction = ${fparse (SiC_radius^3 - iPyC_radius^3) / oPyC_radius^3}
opyc_fraction = ${fparse (oPyC_radius^3 - SiC_radius^3) / oPyC_radius^3}
fuel_blocks = 'compacts compacts_trimmer_tri'
[Mesh]
[mesh]
type = FileMeshGenerator
file = solid_mesh_in.e
[]
[delete_coolant]
type = BlockDeletionGenerator
input = mesh
block = 'coolant'
[]
[]
[Variables]
[T]
initial_condition = ${inlet_T}
[]
[]
[Kernels]
[diffusion]
type = HeatConduction
variable = T
[]
[source]
type = CoupledForce
variable = T
v = power
block = ${fuel_blocks}
[]
[]
[BCs]
[pin_outer]
type = MatchedValueBC
variable = T
v = fluid_temp
boundary = 'fluid_solid_interface'
[]
[]
[Functions]
[k_graphite]
type = ParsedFunction
expression = '${matrix_k}'
[]
[k_TRISO]
type = ParsedFunction
expression = '${kernel_fraction} * ${kernel_k} + ${buffer_fraction} * ${buffer_k} + ${fparse ipyc_fraction + opyc_fraction} * ${PyC_k} + ${sic_fraction} * ${SiC_k}'
[]
[k_compacts]
type = ParsedFunction
expression = '${triso_pf} * k_TRISO + ${fparse 1.0 - triso_pf} * k_graphite'
symbol_names = 'k_TRISO k_graphite'
symbol_values = 'k_TRISO k_graphite'
[]
[]
[Materials]
[graphite]
type = HeatConductionMaterial
thermal_conductivity_temperature_function = k_graphite
temp = T
block = 'graphite'
[]
[compacts]
type = HeatConductionMaterial
thermal_conductivity_temperature_function = k_compacts
temp = T
block = ${fuel_blocks}
[]
[]
[Postprocessors]
[flux_integral] # evaluate the total heat flux for normalization
type = SideDiffusiveFluxIntegral
diffusivity = thermal_conductivity
variable = T
boundary = 'fluid_solid_interface'
[]
[max_fuel_T]
type = ElementExtremeValue
variable = T
value_type = max
block = ${fuel_blocks}
[]
[max_block_T]
type = ElementExtremeValue
variable = T
value_type = max
block = 'graphite'
[]
[power]
type = ElementIntegralVariablePostprocessor
variable = power
block = ${fuel_blocks}
execute_on = 'transfer'
[]
[]
[AuxVariables]
[fluid_temp]
[]
[flux]
family = MONOMIAL
order = CONSTANT
[]
[power]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[flux]
type = DiffusionFluxAux
diffusion_variable = T
component = normal
diffusivity = thermal_conductivity
variable = flux
boundary = 'fluid_solid_interface'
[]
[]
[Executioner]
type = Transient
nl_abs_tol = 1e-5
nl_rel_tol = 1e-16
petsc_options_value = 'hypre boomeramg'
petsc_options_iname = '-pc_type -pc_hypre_type'
[]
[UserObjects]
[average_fuel_axial]
type = LayeredAverage
variable = T
direction = z
num_layers = ${num_layers_for_plots}
block = ${fuel_blocks}
[]
[average_block_axial]
type = LayeredAverage
variable = T
direction = z
num_layers = ${num_layers_for_plots}
block = 'graphite'
[]
[]
[VectorPostprocessors]
[fuel_axial_avg]
type = SpatialUserObjectVectorPostprocessor
userobject = average_fuel_axial
[]
[block_axial_avg]
type = SpatialUserObjectVectorPostprocessor
userobject = average_block_axial
[]
[]
[Outputs]
exodus = true
print_linear_residuals = false
[csv]
type = CSV
file_base = 'csv_thm/solid_out'
[]
[]
Fluid Input Files
The fluid mass, momentum, and energy transport physics are solved using THM. The input file for this portion of the physics is the thm.i input. The THM input file is built using syntax specific to THM - we will only briefly cover the syntax, and instead refer users to the THM documentation for more information. First, we define a number of constants at the beginning of the file and apply some global settings. We set the initial conditions for pressure, velocity, and temperature and indicate the fluid EOS object using IdealGasFluidProperties.
# copy-pasta from common.i
inlet_T = 598.0 # inlet fluid temperature (K)
mdot = ${fparse 117.3 / 12 / 108} # fluid mass flowrate (kg/s)
outlet_P = 7.1e6 # fluid outlet pressure (Pa)
channel_diameter = 0.016 # diameter of the coolant channels (m)
unit_cell_height = 1.6 # unit cell height - arbitrarily selected
num_layers_for_THM = 150
[GlobalParams]
initial_p = ${outlet_P}
initial_T = ${inlet_T}
initial_vel = ${fparse mdot / outlet_P / 8.3144598 * 4.0e-3 / inlet_T / (pi * channel_diameter * channel_diameter / 4.0)}
rdg_slope_reconstruction = full
closures = none
fp = helium
[]
[Closures]
[none]
type = Closures1PhaseNone
[]
[]
[FluidProperties]
[helium]
type = IdealGasFluidProperties
molar_mass = 4e-3
gamma = 1.668282 # should correspond to Cp = 5189 J/kg/K
k = 0.2556
mu = 3.22639e-5
[]
[]
Next, we define the "components" in the domain. These components essentially consist of the physics equations and boundary conditions solved by THM, but expressed in THM-specific syntax. These components define single-phase flow in a pipe, an inlet mass flowrate boundary condition, an outlet pressure condition, and heat transfer to the pipe wall.
[Components]
[channel]
type = FlowChannel1Phase
position = '0 0 0'
orientation = '0 0 1'
A = '${fparse pi * channel_diameter * channel_diameter / 4}'
D_h = ${channel_diameter}
length = ${unit_cell_height}
n_elems = ${num_layers_for_THM}
[]
[inlet]
type = InletMassFlowRateTemperature1Phase
input = 'channel:in'
m_dot = ${mdot}
T = ${inlet_T}
[]
[outlet]
type = Outlet1Phase
input = 'channel:out'
p = ${outlet_P}
[]
[ht_ext]
type = HeatTransferFromExternalAppHeatFlux1Phase
flow_channel = channel
P_hf = '${fparse channel_diameter * pi}'
[]
[]
Associated with these components are a number of closures, defined as materials. We set up the Churchill correlation for the friction factor and the Dittus-Boelter correlation for the convective heat transfer coefficient. For the Dittus-Boelter correlation, we use a corrected version of the closure (with the leading coefficient changed from 0.023 to 0.021) based on the NekRS simulations described in an earlier tutorial. Additional materials are created to represent dimensionless numbers and other auxiliary terms, such as the wall temperature. As can be seen here, the Material system is not always used to represent quantities traditioanlly thought of as "material properties."
[Materials]
# wall friction closure
[f_mat]
type = ADWallFrictionChurchillMaterial
block = channel
D_h = D_h
f_D = f_D
vel = vel
rho = rho
mu = mu
[]
# Wall heat transfer closure (all important is in Nu_mat)
[Re_mat]
type = ADReynoldsNumberMaterial
block = channel
Re = Re
D_h = D_h
mu = mu
vel = vel
rho = rho
[]
[Pr_mat]
type = ADPrandtlNumberMaterial
block = channel
cp = cp
mu = mu
k = k
[]
[Nu_mat]
type = ADParsedMaterial
block = channel
# Dittus-Boelter
expression = '0.021 * pow(Re, 0.8) * pow(Pr, 0.4)'
property_name = 'Nu'
material_property_names = 'Re Pr'
[]
[Hw_mat]
type = ADConvectiveHeatTransferCoefficientMaterial
block = channel
D_h = D_h
Nu = Nu
k = k
[]
[T_wall]
type = ADTemperatureWall3EqnMaterial
Hw = Hw
T = T
q_wall = q_wall
[]
[]
THM computes the wall temperature to apply a boundary condition in the MOOSE heat transfer module. To convert the T_wall material into an auxiliary variable, we use the ADMaterialRealAux.
[AuxVariables]
[T_wall]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[Tw_aux]
type = ADMaterialRealAux
block = channel
variable = T_wall
property = T_wall
[]
[]
Finally, we set the preconditioner, a Transient executioner, and set an Exodus output. We will run THM to convergence based on a tight steady state relative tolerance of .
[Preconditioning]
[pc]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
dt = 0.1
steady_state_detection = true
steady_state_tolerance = 1e-08
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
solve_type = NEWTON
line_search = basic
[]
[Outputs]
exodus = true
print_linear_residuals = false
[console]
type = Console
outlier_variable_norms = false
[]
[csv]
type = CSV
file_base = 'csv_thm/thm'
[]
[]
Execution and Postprocessing
To run the coupled OpenMC-NekRS-MOOSE calculation, run the following:
mpiexec -np 500 cardinal-opt -i common_input.i openmc_nek.i
This will run with 500 Message Passing Interface (MPI) processes (you may run with other parallel configurations as needed, but you will find that the NekRS simulation requires HPC resources due to the large mesh). To run the coupled OpenMC-THM-MOOSE calculation, run the following:
mpiexec -np 2 cardinal-opt -i common_input.i openmc_thm.i --n-threads=36
which will run with 2 MPI ranks with 36 threads each (again, these parallel resource choices are only examples). When the two simulations have completed, you will have created a number of different output files. For the OpenMC-NekRS-MOOSE calculation:
openmc_nek_out.e, an Exodus file with the OpenMC solutionopenmc_nek_out_bison0.e, an Exodus file with the MOOSE heat conduction solutionopenmc_nek_out_bison0_nek0.e, an Exodus file with the NekRS solutioncsv_nek/*, CSV files with various postprocessors and userobjects
And for the OpenMC-THM-MOOSE calculation:
openmc_thm_out.e, an Exodus file with the OpenMC solutionopenmc_thm_out_bison0.e, an Exodus file with the MOOSE heat conduction solutionopenmc_thm_out_thm0.e, an Exodus file with the THM solutioncsv_thm/*, CSV files with various postprocessors and userobjects
We now briefly present the coupled physics predictions. Figure 6 shows the fission power predicted by OpenMC with thermal-fluid feedback from NekRS-MOOSE and THM-MOOSE. Also shown is the difference between the two predictions (NekRS case minus the THM case). For the six compacts with 50 axial cell layers, the OpenMC model contains a total of 300 tallies; the maximum tally relative error of 1% does introduce some slight asymmetries among the six compacts, which are easiest to discern in the "difference" image in Figure 6.
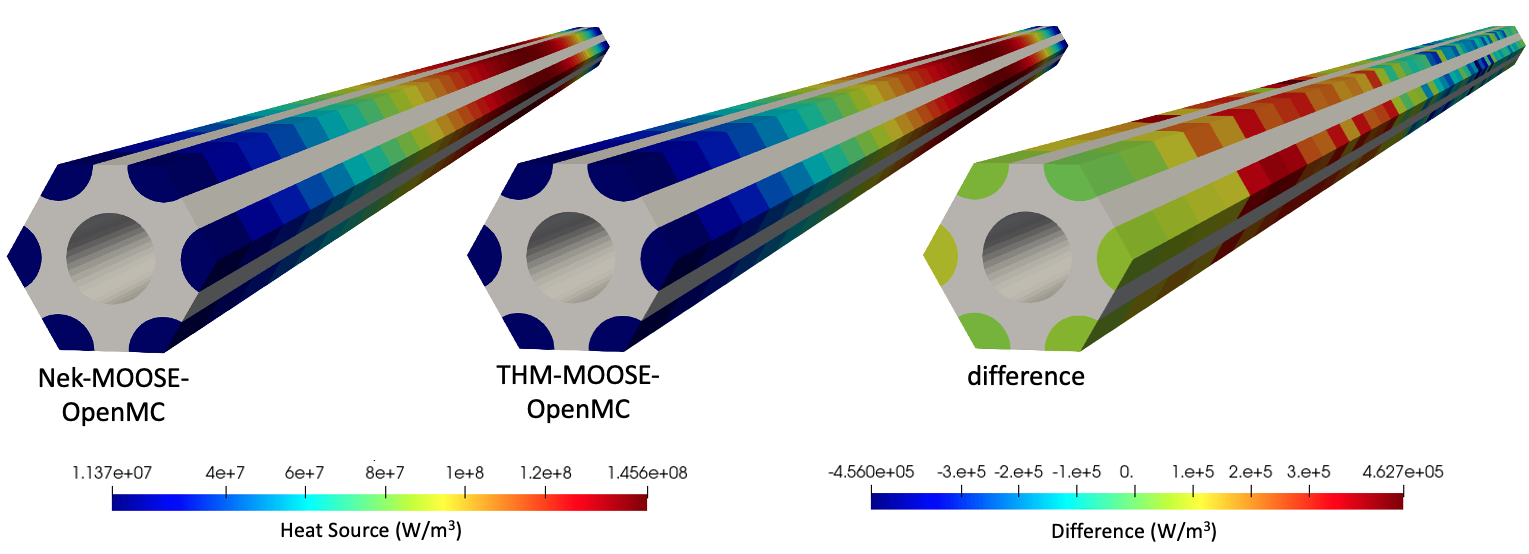
Figure 6: Heat source predicted by OpenMC with thermal feedback from either NekRS-MOOSE or THM-MOOSE
The lack of reflectors results in a relatively high leakage percentage of about 18.8%. For the unit cell, recall that the fluid temperature rise is only 82 K. These two effects combine to give a power distribution that is very nearly symmetric in the axial direction - while the lower solid temperatures near the inlet do cause power to shift slightly downwards, the magnitude of the shift is moderated by the effect of pushing the fission source closer to external boundaries, where those neutrons would be more likely to exit the domain.
In the earlier conjugate heat transfer tutorial, we showed that CHT calculations with NekRS-MOOSE and THM-MOOSE agree very well with one another in terms of fluid temperature, solid temperature, and fluid density. Especially when considering that the neutronics feedback due to fluid temperature and density are very small for gas-cooled systems, the excellent agreement in OpenMC's fission distribution shown in Figure 6 is as expected. When cast in terms of a percent difference (as opposed to the absolute difference shown in Figure 6), the NekRS-MOOSE-OpenMC and THM-MOOSE-OpenMC cases agree to within 1%, which is within the range of the uncertainty in the fission tally itself.
Figure 7 shows the solid temperature predicted by the MOOSE heat transfer module, with physics feedback provided by either NekRS-OpenMC or THM-OpenMC. The solid temperature peaks slightly downstream of the maximum OpenMC power due to the combined effects of the power distribution and convective heat transfer at the wall. Figure 7 helps explain the trend in the power difference shown in Figure 6. Near the inlet, NekRS predicts a lower temperature than THM, while near the outlet NekRS predicts a higher temperature than THM. Due to the negative temperature reactivity coefficient of the unit cell, this causes the NekRS-based coupled model to predict a higher power than THM near the inlet, but a lower power than THM near the outlet.
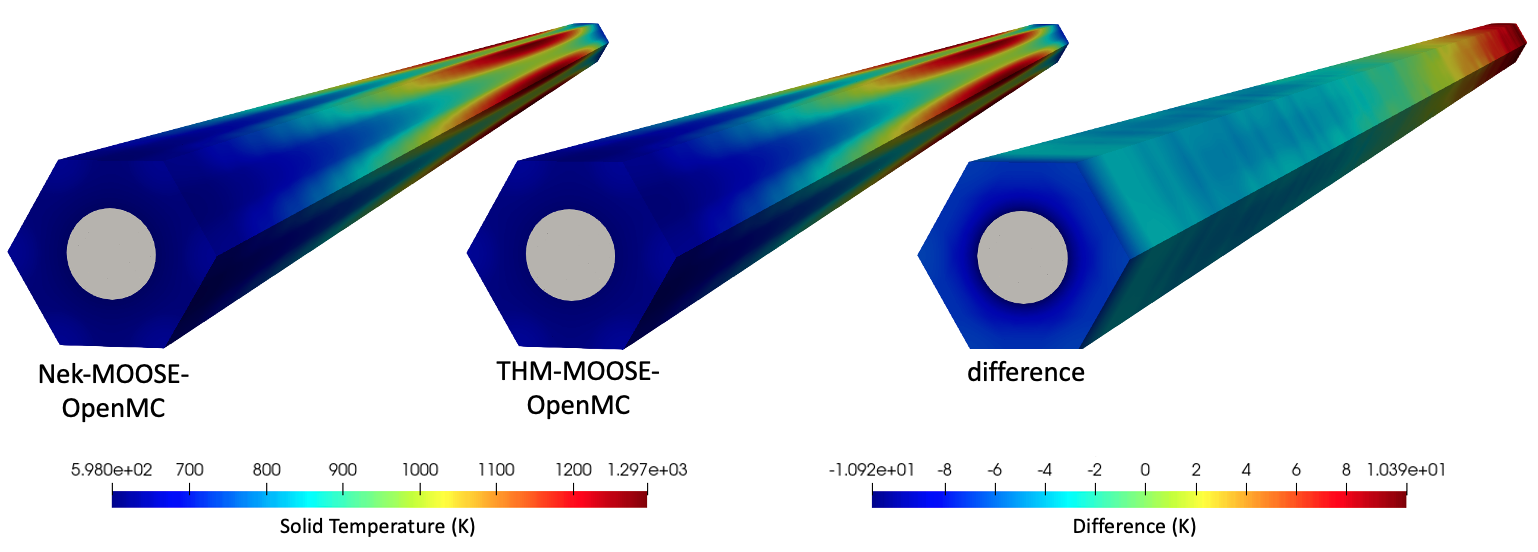
Figure 7: Solid temperature predicted by the MOOSE heat transfer module with physics feedback from either OpenMC-NekRS or OpenMC-THM.
Figure 8 shows the solid temperature predictions on the axial midplane with physics feedback provided by either NekRS-OpenMC or THM-OpenMC. Also shown is the difference between the two (NekRS-based case minus the THM-based case). The THM simulations are unable to capture the radial variation in heat flux along the channel wall, causing THM to underpredict temperatures near the channel wall close to the fuel compacts. However, an additional source of difference is now also present - small radial asymmetries in OpenMC's fission distribution contribute a small asymmetry in solid temperature on the order of 2 K. The tolerance on the fission power uncertainty can simply be increased in order to push down this contribution.
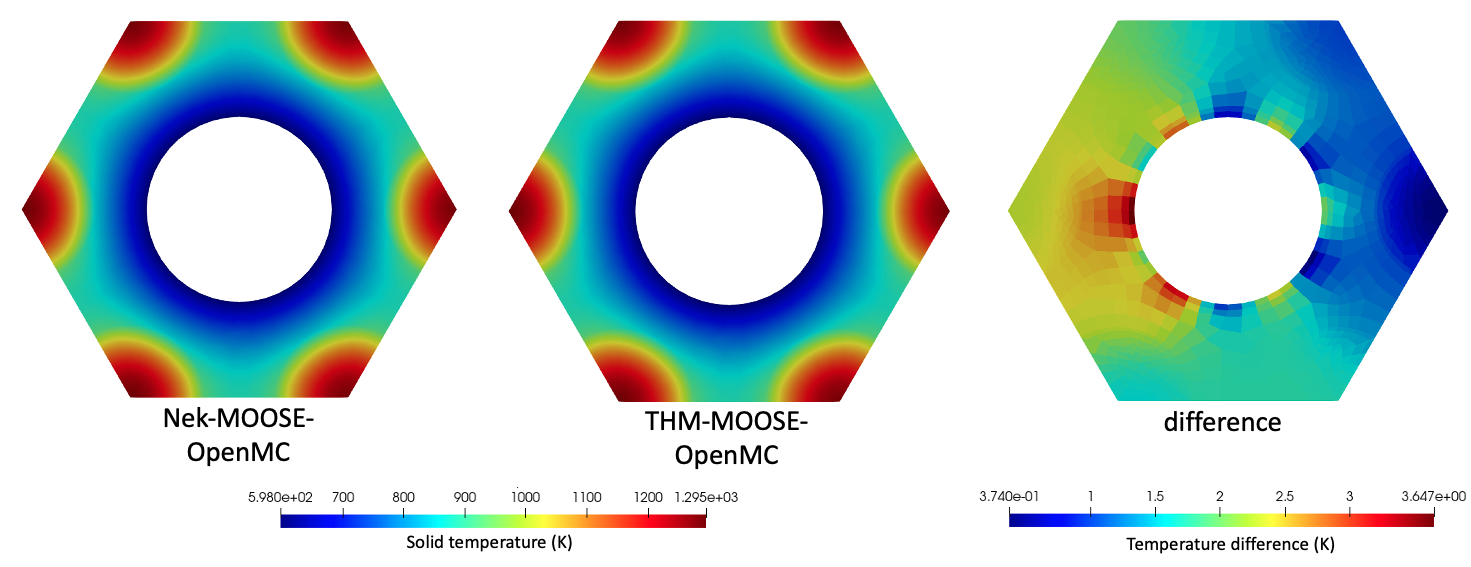
Figure 8: Solid temperature predicted by the MOOSE heat transfer module with physics feedback from either OpenMC-NekRS or OpenMC-THM on the axial mid-plane.
On each axial layer, the OpenMC model receives a total of 14 temperatures (six compacts plus six graphite regions around them, one graphite cell surrounding the coolant channel, and the coolant channel). Figure 9 shows the solid temperature predicted by the NekRS-MOOSE-OpenMC high-resolution simulations along with the actual cell temperature imposed in OpenMC for a half-height slice of the unit cell. OpenMC sets a volume-average temperature for each cell according to the mesh mirror element centroid mappings to OpenMC's cells.
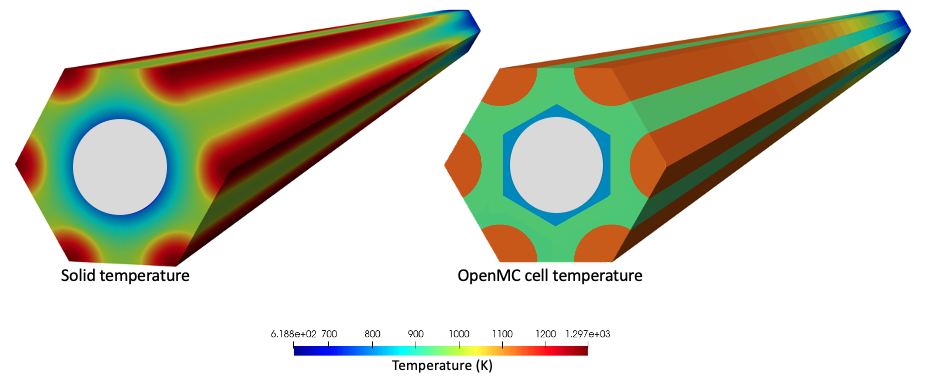
Figure 9: Solid temperature predicted by the MOOSE heat transfer module with physics feedback from OpenMC-NekRS and the solid temperature actually imposed in OpenMC for a half-height portion of the unit cell
Figure 10 shows the fluid temperature predicted by NekRS and THM, with physics feedback provided by MOOSE-OpenMC. NekRS resolves the thermal boundary layer, whereas the THM model uses the Dittus-Boelter correlation to represent the temperature drop from the heated wall to the bulk. Therefore, the fluid temperature shown in Figure 10 for THM is the area-averaged fluid temperature. The wall temperature predicted by NekRS follows a very similar distribution as the heat flux, with a profile that peaks slightly downstream of the maximum power due to the combined effects of convective heat transfer and the fission power distribution.
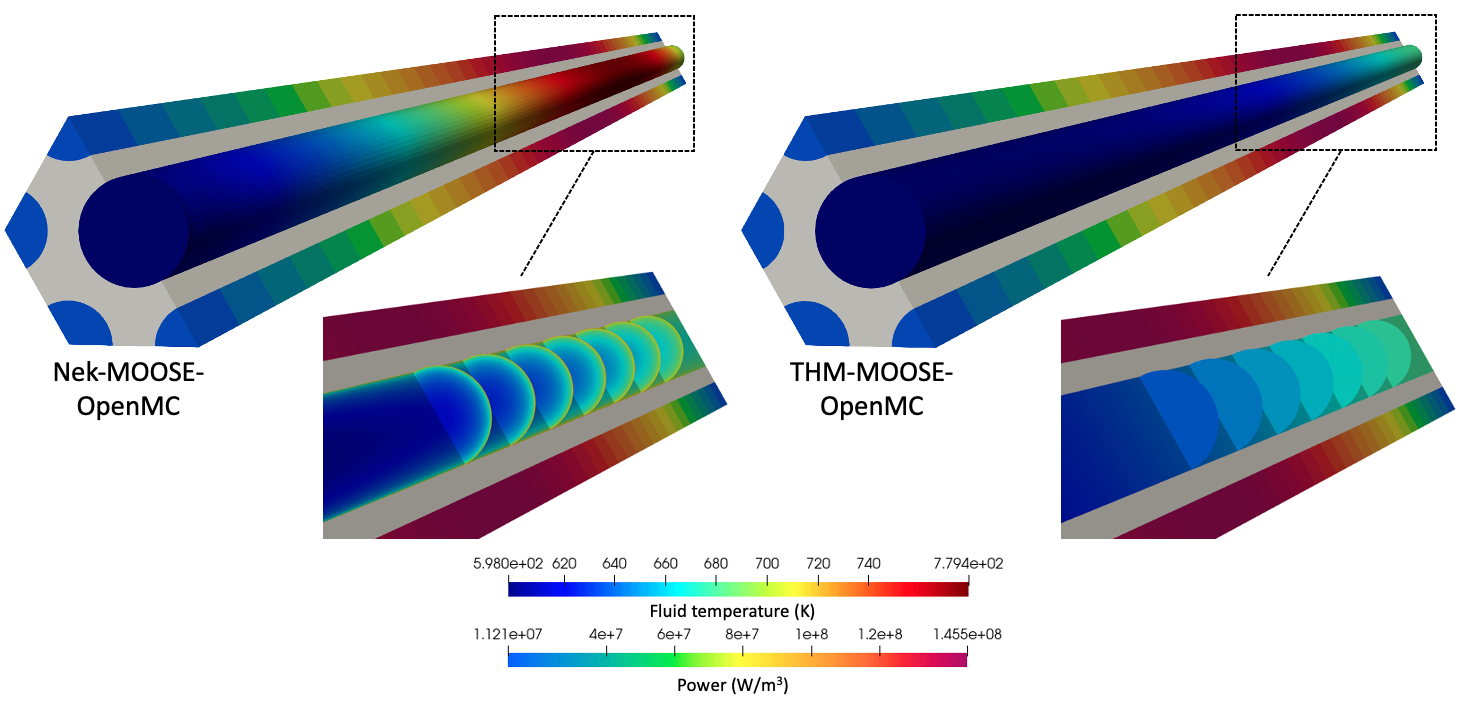
Figure 10: Fluid temperature predicted for the multiphysics simulations for NekRS-MOOSE-OpenMC and THM-MOOSE-OpenMC.
Figure 11 shows the radially-averaged temperatures for the two thermal-fluid feedback options. The fluid bulk temperature increases along the flow direction, with a faster rate of increase where the power density is highest.
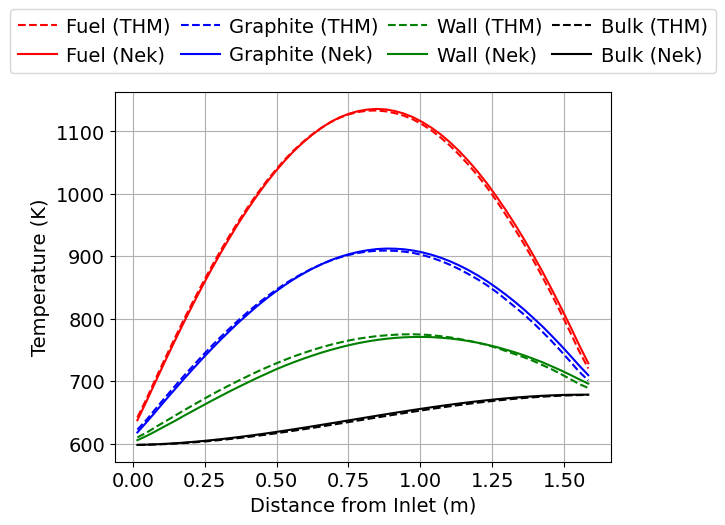
Figure 11: Radially-averaged temperatures for the NekRS-MOOSE-OpenMC and THM-MOOSE-OpenMC simulations.
References
- INL.
High-Temperature Gas-Cooled Test Reactor Point Design.
Technical Report INL/EXT-16-38296, Idaho National Laboratory, 2016.
URL: https://tinyurl.com/v9a4hym5.[BibTeX]
- A.J. Novak, D. Andrs, P. Shriwise, J. Fang, H. Yuan, D. Shaver, E. Merzari, P.K. Romano, and R.C. Martineau.
Coupled Monte Carlo and Thermal-Fluid Modeling of High Temperature Gas Reactors Using Cardinal.
Annals of Nuclear Energy, 177:109310, 2022.
doi:10.1016/j.anucene.2022.109310.[BibTeX]