Conjugate Heat Transfer for Laminar Pin Bundle Flow

In this tutorial, you will learn how to:

Couple NekRS with MOOSE for CHT in a 7-pin bundle
Use different CHT boundary conditions
Control how flux normalization is performed in NekRS (by either lumping all sidesets together, or preserving for each sideset individually)
Reduce the amount of copy to/from commands between host and device for NekRS (an advanced user feature)

To access this tutorial,


cd cardinal/tutorials/sfr_7pin

This tutorial also requires you to download a mesh file from Box. Please download the files from the sfr_7pin folder here and place these files within the same directory structure in tutorials/sfr_7pin.

Geometry and Computational Model

The geometry is a shorter, 7-pin version of the fuel bundles in the Advanced Burner Test Reactor (ABTR) Cahalan et al. (2006). Relevant dimensions are summarized in Table 1.

Table 1: Geometric and operating conditions for the ABTR, based on Cahalan et al. (2006)

Parameter	Value
Pellet diameter	6.03 mm
Clad diameter	8.00 mm
Clad thickness	0.52 mm
Height	0.2032 m
Flat-to-flat distance inside duct	0.02625 m
Bundle power	21 kW
Core inlet temperature	355°C
Mass flowrate	0.1 kg/s
Coolant	sodium

Heat Conduction Model

The MOOSE heat transfer module is used to solve for energy conservation in the solid. The tops and bottoms of the pins and ducts are insulated. The outer boundary condition on the duct is a convective cooling boundary condition.

The gap region between the pellet and the cladding is unmeshed, and a quadrature-based thermal contact model is applied based on the sum of thermal conduction and thermal radiation (across a transparent medium). For a paired set of boundaries, each quadrature point on boundary $var element = document.getElementById("moose-equation-6b631b72-5317-4b1b-8f29-e3e95daca91f");katex.render("A", element, {displayMode:false,throwOnError:false});$ is paired with the nearest quadrature point on boundary B. Then, the sum of the radiation and conduction heat fluxes imposed between pairs of quadrature points is

$(1)var element = document.getElementById("moose-equation-54afeb43-e7f1-47a5-b2c4-a37b034468f0");katex.render(" q^{''}=\\sigma\\frac{T^4-T_{gap}^4}{\\frac{1}{\\sigma_A}+\\frac{1}{\\sigma_B}-1}+\\frac{T-T_{gap}}{r_{th}}", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-23d29849-b47c-463c-8882-6bb87f9859a1");katex.render("\\sigma", element, {displayMode:false,throwOnError:false});$ is the Stefan-Boltzmann constant, $var element = document.getElementById("moose-equation-17658219-46d1-4026-92f7-7c19de785cb3");katex.render("T", element, {displayMode:false,throwOnError:false});$ is the temperature at a quadrature point, $var element = document.getElementById("moose-equation-cbc42c8d-4166-4549-a7e1-0f9c7d004973");katex.render("T_{gap}", element, {displayMode:false,throwOnError:false});$ is the temperature of the nearest quadrature point across the gap, $var element = document.getElementById("moose-equation-ac8313d9-1044-4ecd-af16-3063c627c3cc");katex.render("\\sigma_A", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-ba9cc11b-c2ef-4be5-8786-95dcb706d4ad");katex.render("\\sigma_B", element, {displayMode:false,throwOnError:false});$ are emissivities of boundaries $var element = document.getElementById("moose-equation-23ff09be-efd5-429e-8602-f63e3a641c85");katex.render("A", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-78060d70-1cb1-48f3-af72-d3ff09e383fd");katex.render("B", element, {displayMode:false,throwOnError:false});$ , respectively, and $var element = document.getElementById("moose-equation-7f6a2d27-fbe4-437d-9dd7-a4a4b05e3397");katex.render("r_{th}", element, {displayMode:false,throwOnError:false});$ is the conduction resistance. For cylinders, the conduction is

$(2)var element = document.getElementById("moose-equation-70b8cf1e-3a19-401d-840b-8bf992de2222");katex.render(" r_{th}=\\frac{\\ln{\\left(\\frac{r_2}{r_1}\\right)}}{2\\pi L k}", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-dbb7dd31-3f91-4e21-9374-636946fff575");katex.render("r_2>r_1", element, {displayMode:false,throwOnError:false});$ are the outer and inner radii of the cylindrical annulus, $var element = document.getElementById("moose-equation-fb46f97b-a3f8-4cdc-9f3b-15fbe5830c9f");katex.render("L", element, {displayMode:false,throwOnError:false});$ is the height of the annulus, and $var element = document.getElementById("moose-equation-d4fc674b-d489-4cb2-b5b0-cdcf8d969082");katex.render("k", element, {displayMode:false,throwOnError:false});$ is the thermal conductivity of the annulus material.

In this tutorial, we will demonstrate two different CHT coupling options for the boundary condition on the fuel pin surfaces and the duct inner boundary (the boundaries in contact with a modeled fluid):

"Cond. Flux - Temperature" in Cond. Flux-Temperature CHT Coupling boundary condition applied to the solid is wall temperature
"Cond. Flux - Conv. Flux" in Cond. Flux-Conv. Flux Coupling Option : boundary condition applied to the solid is wall convective flux

The "Cond. Flux - Temperature" option will be described first, and then sections towards the end will describe the modifications necessary to use alternate CHT boundary conditions.

NekRS Model

NekRS is used to solve the incompressible Navier-Stokes equations. The inlet velocity is selected such that the mass flowrate is 0.1 kg/s, which is low enough that the flow is laminar and a turbulence model is not required. At the outlet, a zero (gage) pressure is imposed and an outflow condition is applied for the energy conservation equation. On all solid-fluid interfaces, the velocity is set to the no-slip condition. The boundary conditions on the pin outer surface and the duct inner surface depends on the CHT boundary conditions:

"Cond. Flux - Temperature" in Cond. Flux-Temperature CHT Coupling : boundary condition applied to NekRs is wall conductive flux
"Cond. Flux - Conv. Flux" in Cond. Flux-Conv. Flux Coupling Option : boundary condition applied to NekRS is wall conductive flux

The initial pressure is set to zero. Both the velocity and temperature are set to uniform initial conditions that match the inlet conditions.

Meshing

Solid Mesh

MOOSE MeshGenerators are used to generate the meshes for the solid. The same solid mesh will be used in the various different models in this tutorial, so we place the content to generate the mesh in mesh.i, and then include it from within the other files.

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]

# --- DUCT --- #

  # Make the duct mesh in 2-D; we first create a "solid" hexagon with two blocks
  # so that we can set the inner wall sideset as the boundary between these two blocks,
  # and then delete an inner block to get just the duct walls
  [duct]
    type = PolygonConcentricCircleMeshGenerator<<<{"description": "This PolygonConcentricCircleMeshGenerator object is designed to mesh a polygon geometry with optional rings centered inside.", "href": "../source/meshgenerators/PolygonConcentricCircleMeshGenerator.html"}>>>
    num_sides<<<{"description": "Number of sides of the polygon."}>>> = 6
    polygon_size<<<{"description": "Size of the polygon to be generated (given as either apothem or radius depending on polygon_size_style)."}>>> = ${fparse bundle_pitch / 2.0 + duct_thickness}
    num_sectors_per_side<<<{"description": "Number of azimuthal sectors per polygon side (rotating counterclockwise from top right face)."}>>> = '14 14 14 14 14 14'
    uniform_mesh_on_sides<<<{"description": "Whether the side elements are reorganized to have a uniform size."}>>> = true

    duct_sizes<<<{"description": "Distance(s) from polygon center to duct(s) inner boundaries."}>>> = '${fparse bundle_pitch / 2.0}'
    duct_block_ids<<<{"description": "Optional customized block ids for each duct geometry block."}>>> = '10'
    duct_intervals<<<{"description": "Number of meshing intervals in each enclosing duct excluding duct boundary layers."}>>> = '4'
    duct_sizes_style<<<{"description": "Style in which polygon center to duct inner boundary distance is given (apothem = center to face, radius = center to vertex). Options: apothem radius"}>>> = apothem
  []
  [inner_sideset]
    type = SideSetsBetweenSubdomainsGenerator<<<{"description": "MeshGenerator that creates a sideset composed of the nodes located between two or more subdomains.", "href": "../source/meshgenerators/SideSetsBetweenSubdomainsGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = duct
    new_boundary<<<{"description": "The list of boundary names to create on the supplied subdomain"}>>> = '10'
    primary_block<<<{"description": "The primary set of blocks for which to draw a sideset between"}>>> = '10'
    paired_block<<<{"description": "The paired set of blocks for which to draw a sideset between"}>>> = '1'
  []
  [delete_inside_block]
    type = BlockDeletionGenerator<<<{"description": "Mesh generator which removes elements from the specified subdomains", "href": "../source/meshgenerators/BlockDeletionGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = inner_sideset
    block<<<{"description": "The list of blocks to be deleted"}>>> = '1'
  []

  # rotate the duct by 30 degrees, then add names for sidesets. Delete sideset 1 because
  # we will name some other part of our mesh with sideset 1.
  [rotate]
    type = TransformGenerator<<<{"description": "Applies a linear transform to the entire mesh.", "href": "../source/meshgenerators/TransformGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = delete_inside_block
    transform<<<{"description": "The type of transformation to perform (TRANSLATE, TRANSLATE_CENTER_ORIGIN, TRANSLATE_MIN_ORIGIN, ROTATE, SCALE)"}>>> = rotate
    vector_value<<<{"description": "The value to use for the transformation. When using TRANSLATE or SCALE, the xyz coordinates are applied in each direction respectively. When using ROTATE, the values are interpreted as the Euler angles phi, theta and psi given in degrees."}>>> = '30.0 0.0 0.0'
  []
  [rename_sideset_names]
    type = RenameBoundaryGenerator<<<{"description": "Changes the boundary IDs and/or boundary names for a given set of boundaries defined by either boundary ID or boundary name. The changes are independent of ordering. The merging of boundaries is supported.", "href": "../source/meshgenerators/RenameBoundaryGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = rotate
    old_boundary<<<{"description": "Elements with these boundary ID(s)/name(s) will be given the new boundary information specified in 'new_boundary'"}>>> = '10000 10'
    new_boundary<<<{"description": "The new boundary ID(s)/name(s) to be given by the boundary elements defined in 'old_boundary'."}>>> = 'duct_outer duct_inner'
  []
  [delete_extraneous]
    type = BoundaryDeletionGenerator<<<{"description": "Mesh generator which removes side sets", "href": "../source/meshgenerators/BoundaryDeletionGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = rename_sideset_names
    boundary_names<<<{"description": "The boundaries to be deleted / kept"}>>> = '1'
  []

# --- CLAD --- #

  [clad]
    type = AnnularMeshGenerator<<<{"description": "For rmin>0: creates an annular mesh of QUAD4 elements. For rmin=0: creates a disc mesh of QUAD4 and TRI3 elements. Boundary sidesets are created at rmax and rmin, and given these names. If dmin!=0 and dmax!=360, a sector of an annulus or disc is created. In this case boundary sidesets are also created at dmin and dmax, and given these names", "href": "../source/meshgenerators/AnnularMeshGenerator.html"}>>>
    nr<<<{"description": "Number of elements in the radial direction"}>>> = 3
    nt<<<{"description": "Number of elements in the angular direction"}>>> = 20
    rmin<<<{"description": "Inner radius.  If rmin=0 then a disc mesh (with no central hole) will be created."}>>> = ${fparse d_pin / 2.0 - t_clad}
    rmax<<<{"description": "Outer radius"}>>> = ${fparse d_pin / 2.0}
    quad_subdomain_id<<<{"description": "The subdomain ID given to the QUAD4 elements"}>>> = 1
    tri_subdomain_id<<<{"description": "The subdomain ID given to the TRI3 elements (these exist only if rmin=0, and they exist at the center of the disc"}>>> = 0
  []
  [rename_clad] # this renames some sidesets on the clad to avoid name clashes
    type = RenameBoundaryGenerator<<<{"description": "Changes the boundary IDs and/or boundary names for a given set of boundaries defined by either boundary ID or boundary name. The changes are independent of ordering. The merging of boundaries is supported.", "href": "../source/meshgenerators/RenameBoundaryGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = clad
    old_boundary<<<{"description": "Elements with these boundary ID(s)/name(s) will be given the new boundary information specified in 'new_boundary'"}>>> = '1 0' # outer surface, inner surface
    new_boundary<<<{"description": "The new boundary ID(s)/name(s) to be given by the boundary elements defined in 'old_boundary'."}>>> = '5 4'
  []
  [rename_clad_names] # this renames some names on the clad to avoid name clashes
    type = RenameBoundaryGenerator<<<{"description": "Changes the boundary IDs and/or boundary names for a given set of boundaries defined by either boundary ID or boundary name. The changes are independent of ordering. The merging of boundaries is supported.", "href": "../source/meshgenerators/RenameBoundaryGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = rename_clad
    old_boundary<<<{"description": "Elements with these boundary ID(s)/name(s) will be given the new boundary information specified in 'new_boundary'"}>>> = '5 4' # outer surface, inner surface
    new_boundary<<<{"description": "The new boundary ID(s)/name(s) to be given by the boundary elements defined in 'old_boundary'."}>>> = 'clad_outer clad_inner'
  []

# --- FUEL --- #

  [fuel]
    type = AnnularMeshGenerator<<<{"description": "For rmin>0: creates an annular mesh of QUAD4 elements. For rmin=0: creates a disc mesh of QUAD4 and TRI3 elements. Boundary sidesets are created at rmax and rmin, and given these names. If dmin!=0 and dmax!=360, a sector of an annulus or disc is created. In this case boundary sidesets are also created at dmin and dmax, and given these names", "href": "../source/meshgenerators/AnnularMeshGenerator.html"}>>>
    nr<<<{"description": "Number of elements in the radial direction"}>>> = 10
    nt<<<{"description": "Number of elements in the angular direction"}>>> = 20
    rmin<<<{"description": "Inner radius.  If rmin=0 then a disc mesh (with no central hole) will be created."}>>> = 0
    rmax<<<{"description": "Outer radius"}>>> = ${fparse d_pellet / 2.0}
    quad_subdomain_id<<<{"description": "The subdomain ID given to the QUAD4 elements"}>>> = 2
    tri_subdomain_id<<<{"description": "The subdomain ID given to the TRI3 elements (these exist only if rmin=0, and they exist at the center of the disc"}>>> = 3
    growth_r<<<{"description": "The ratio of radial sizes of successive rings of elements"}>>> = -1.2
  []

# --- COMBINE --- #

  [combine] # this combines the fuel and clad together to make one pin
    type = CombinerGenerator<<<{"description": "Combine multiple meshes (or copies of one mesh) together into one (disjoint) mesh.  Can optionally translate those meshes before combining them.", "href": "../source/meshgenerators/CombinerGenerator.html"}>>>
    inputs<<<{"description": "The input MeshGenerators.  This can either be N generators or 1 generator.  If only 1 is given then 'positions' must also be given."}>>> = 'rename_clad_names fuel'
  []
  [repeat] # this repeats the pincell 7 times to get the 7 pins, and adds the duct
    type = CombinerGenerator<<<{"description": "Combine multiple meshes (or copies of one mesh) together into one (disjoint) mesh.  Can optionally translate those meshes before combining them.", "href": "../source/meshgenerators/CombinerGenerator.html"}>>>
    inputs<<<{"description": "The input MeshGenerators.  This can either be N generators or 1 generator.  If only 1 is given then 'positions' must also be given."}>>> = 'combine combine combine combine combine combine combine delete_extraneous'
    positions<<<{"description": "The (optional) position of each given mesh.  If N 'inputs' were given then this must either be left blank or N positions must be given.  If 1 input was given then this MUST be provided."}>>> = '+0.00000000 +0.00000000 +0.00000000
                 +0.00452000 +0.00782887 +0.00000000
                 -0.00452000 +0.00782887 +0.00000000
                 -0.00904000 +0.00000000 +0.00000000
                 -0.00452000 -0.00782887 +0.00000000
                 +0.00452000 -0.00782887 +0.00000000
                 +0.00904000 +0.00000000 +0.00000000
                 +0.0        +0.0        +0.0'
  []
  [extrude]
    type = AdvancedExtruderGenerator<<<{"description": "Extrudes a 1D mesh into 2D, or a 2D mesh into 3D, can have a variable height for each elevation, variable number of layers within each elevation, variable growth factors of axial element sizes within each elevation and remap subdomain_ids, boundary_ids and element extra integers within each elevation as well as interface boundaries between neighboring elevation layers.", "href": "../source/meshgenerators/AdvancedExtruderGenerator.html"}>>>
    input<<<{"description": "The mesh to extrude"}>>> = repeat
    direction<<<{"description": "A vector that points in the direction to extrude (note, this will be normalized internally - so don't worry about it here)"}>>> = '0 0 1'
    num_layers<<<{"description": "The number of layers for each elevation - must be num_elevations in length!"}>>> = '40'
    heights<<<{"description": "The height of each elevation"}>>> = '${L}'
  []
[]

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

The solid mesh is shown in Figure 1; the different regions in this mesh are first created in 2-D, and then extruded into 3-D. You can visualize the mesh when you run the simulations (in the output files), or you can generate it without running the simulation (if you wanted to view it separately from a simulation) by doing

cardinal-opt -i solid.i --mesh-only

which will create the mesh as solid_in.e. The boundary names are illustrated towards the right by showing the highlighted surface to which each boundary corresponds. A unique block ID is used for the set of elements in the cladding, the duct, and for the pellet elements. Two block IDs are required to describe the pellet regions because two different element types (quads and prisms) are present in the pellet region. The pellet-clad gap is unmeshed.

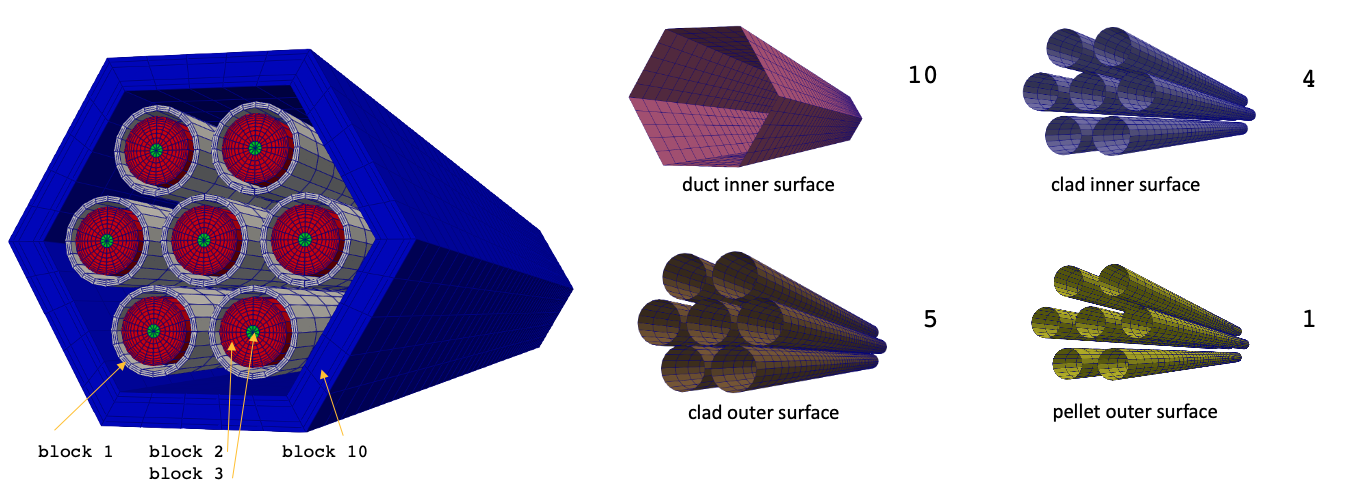
Figure 1: Mesh for the solid portions of the 7-pin bare Sodium Fast Reactor (SFR) bundle

Unique boundary names are set for each boundary to which we will apply a unique boundary condition. Because we will apply insulated boundary conditions on the top and bottom surfaces, as well as on the outside of the duct, we don't need to define sidesets ( the "do-nothing" boundary condition in the finite element method is a zero-flux condition).

Fluid Mesh

The fluid mesh is shown in Figure 2. You can download this mesh from Box, or you can generate it yourself using the meshing scripts in Cardinal.

To generate the mesh yourself, navigate to the cardinal/utils/meshing/assembly directory. The mesh_settings.py file contains a set of configurable parameters to generate this mesh. The settings used for this tutorial are shown below, which will generate a 7-pin mesh in dimensional units and with geometry choices consistent with Table 1.

nondimensional = False        # whether to generate the mesh in non-dimensional form
pin_diameter = 8e-3           # pin diameter
pin_pitch = 0.00904           # pin pitch
flat_to_flat = 0.02625        # duct inner flat-to-flat
wire_diameter = 0             # wire diameter
wire_pitch = 0                # wire axial pitch
h = 20.32e-2                  # height
n_pins = 7                    # number of pins

e_per_side = 4                # number of elements along each 1/6 of the pin
e_per_bl = 3                  # number of elements in each boundary layer
e_per_pin_background = 3      # number of background elements in pincell
e_per_assembly_background = 3 # number of background elements in assembly
growth_factor = 1.8           # boundary layer growth factor
nl = 30                       # number of axial layers
bl_height = 0.00006           # height of first boundary layer

# If you would like to apply a radius of curvature to the corners of the
# duct, set the following parameters.
#
# corner_radius: radius of curvature of duct corners
# corner_smoothing: Smoothing factors to apply to the corner movement; must match
#                   the length of the e_per_bl + e_per_assembly_background. You may
#                   need to adjust this parameter if the default doesn't work nicely.
corner_radius = 0
corner_smoothing = '1.0 1.0 1.0 0.75 0.25 0.25'

You can then generate the mesh in exodus format (fluid.exo) and then convert it into NekRS's .re2 format by running


python mesh.py -g
~/Nek5000/bin/exo2nek

The complete fluid mesh is shown in Figure 2. The boundary names are illustrated by showing the highlighted surface to which each corresponds. Note that the meshes in Figure 1 and Figure 2 do not need to share nodes between the fluid and solid boundaries through which CHT coupling will be performed - interpolations using MOOSE's Transfers handle any differences in the mesh.

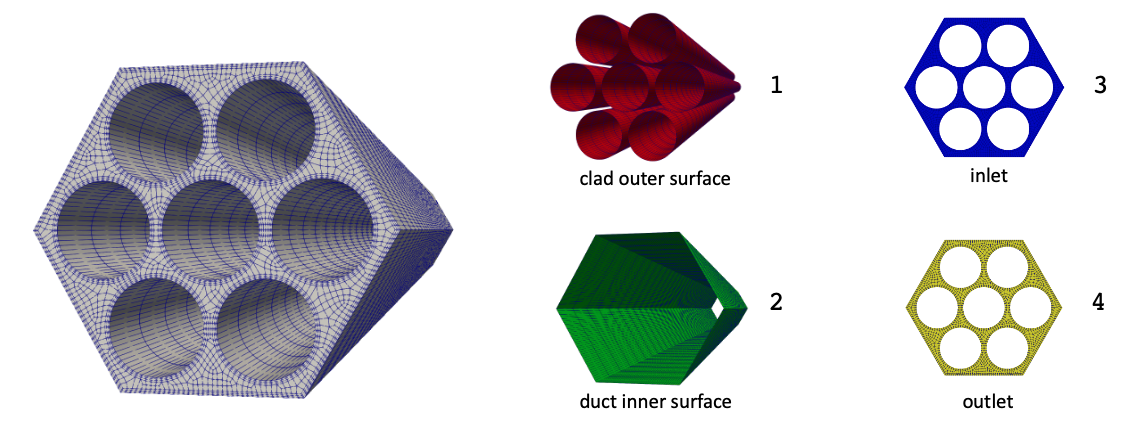
Figure 2: Mesh for the fluid portions of the 7-pin bare SFR bundle

Cond. Flux-Temperature CHT Coupling

In this section, NekRS and MOOSE are coupled for CHT using the "Cond. Flux - Temperature" coupling mode.

Solid Input Files

The solid phase is solved with the MOOSE heat transfer module, and is described in the solid.i input file. At the top of this file, various problem parameters are defined as file-local variables to help with setting up the uniform heat source in the fuel.

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

The heat transfer module will solve for temperature, which is defined as a nonlinear variable.

[Variables<<<{"href": "../syntax/Variables/index.html"}>>>]
  [T]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 500.0
  []
[]

The Transfer system is used to communicate variables across applications; a boundary heat flux will be computed by MOOSE and applied as a boundary condition in NekRS. In the opposite direction, NekRS will compute a surface temperature that will be applied as a boundary condition in MOOSE. Therefore, we define auxiliary variables to hold the flux computed by MOOSE (flux) and the surface temperature received from NekRS (nek_temp).

[AuxVariables<<<{"href": "../syntax/AuxVariables/index.html"}>>>]
  [nek_temp]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 500.0
  []
  [flux]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    block = '1 10'
  []
[]

Next, the governing equation solved by MOOSE is specified with the Kernels block as the HeatConduction kernel with a volumetric heat source in the pellets with the BodyForce kernel. Notice how we can do math with the file-local variables that were defined at the top of the file, with ${fparse <math statement>} syntax.

[Kernels<<<{"href": "../syntax/Kernels/index.html"}>>>]
  [diffusion]
    type = HeatConduction<<<{"description": "Diffusive heat conduction term $-\\nabla\\cdot(k\\nabla T)$ of the thermal energy conservation equation", "href": "../source/kernels/HeatConduction.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
  []
  [source]
    # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce<<<{"description": "Demonstrates the multiple ways that scalar values can be introduced into kernels, e.g. (controllable) constants, functions, and postprocessors. Implements the weak form $(\\psi_i, -f)$.", "href": "../source/kernels/BodyForce.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    function<<<{"description": "A function that describes the body force"}>>> = '${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}'
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '2 3'
  []
[]

For computing the heat flux on the boundaries coupled to NekRS (the clad outer surface and the duct inner surface), we use a DiffusionFluxAux.

[AuxKernels<<<{"href": "../syntax/AuxKernels/index.html"}>>>]
  [flux]
    type = DiffusionFluxAux<<<{"description": "Compute components of flux vector for diffusion problems $(\\vec{J} = -D \\nabla C)$.", "href": "../source/auxkernels/DiffusionFluxAux.html"}>>>
    diffusion_variable<<<{"description": "The name of the variable"}>>> = T
    component<<<{"description": "The desired component of flux."}>>> = normal
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation."}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = flux
    boundary<<<{"description": "The list of boundaries (ids or names) from the mesh where this object applies"}>>> = '5 10'
  []
[]

The GenericConstantMaterial is then used to specify constant values for the thermal conductivity of the pellet, clad, and duct.

[Materials<<<{"href": "../syntax/Materials/index.html"}>>>]
  [clad_and_duct]
    type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = 'thermal_conductivity'
    prop_values<<<{"description": "The values associated with the named properties"}>>> = '26'
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = 'thermal_conductivity'
    prop_values<<<{"description": "The values associated with the named properties"}>>> = '23'
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '2 3'
  []
[]

Next, we define boundary conditions for the solid. Between the pellet surface and the clad inner surface, we impose a thermal contact model as described in Eq. (1). On fluid-solid interfaces, the solid temperature is set equal to the surface temperature computed by NekRS. The convective cooling boundary condition is applied to the duct outer surface.

[ThermalContact<<<{"href": "../syntax/Modules/HeatTransfer/ThermalContact/index.html"}>>>]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs<<<{"href": "../syntax/BCs/index.html"}>>>]
  [pin_and_duct]
    type = MatchedValueBC<<<{"description": "Implements a NodalBC which equates two different Variables' values on a specified boundary.", "href": "../source/bcs/MatchedValueBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    v<<<{"description": "The variable whose value we are to match."}>>> = nek_temp
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC<<<{"description": "Convective heat transfer boundary condition with temperature and heat transfer coefficent given by material properties.", "href": "../source/bcs/ConvectiveHeatFluxBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    T_infinity<<<{"description": "Material property for far-field temperature"}>>> = 600
    heat_transfer_coefficient<<<{"description": "Material property for heat transfer coefficient"}>>> = 1000
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'duct_outer'
  []
[]

Next, the MultiApps and Transfers blocks describe the interaction between Cardinal and MOOSE. The MOOSE heat transfer module is here run as the main application, with the NekRS wrapping run as the sub-application. Three transfers are required to couple Cardinal and MOOSE; the first is a transfer of surface temperature from Cardinal to MOOSE. The second is a transfer of heat flux from MOOSE to Cardinal. And the third is a transfer of the total integrated heat flux from MOOSE to Cardinal (computed as a postprocessor), which is then used internally by NekRS to re-normalize the heat flux (after interpolation onto its GLL points).

[MultiApps<<<{"href": "../syntax/MultiApps/index.html"}>>>]
  [nek]
    type = TransientMultiApp<<<{"description": "MultiApp for performing coupled simulations with the parent and sub-application both progressing in time.", "href": "../source/multiapps/TransientMultiApp.html"}>>>
    input_files<<<{"description": "The input file for each App.  If this parameter only contains one input file it will be used for all of the Apps.  When using 'positions_from_file' it is also admissable to provide one input_file per file."}>>> = 'nek.i'
    sub_cycling<<<{"description": "Set to true to allow this MultiApp to take smaller timesteps than the rest of the simulation.  More than one timestep will be performed for each parent application timestep"}>>> = true
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
  []
[]

[Transfers<<<{"href": "../syntax/Transfers/index.html"}>>>]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = temperature
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_temp
    to_boundaries<<<{"description": "The boundary we are transferring to (if not specified, whole domain is used)."}>>> = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = flux
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = heat_flux
    from_boundaries<<<{"description": "The boundary we are transferring from (if not specified, whole domain is used)."}>>> = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = heat_flux_integral
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = flux_integral
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = transfer_in
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = synchronize
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
[]

In addition to these three transfers necessary to couple NekRS with MOOSE, there is a fourth transfer - synchronize_in, which transfers the synchronize postprocessor to NekRS. This is an optional transfer and is only used for performance reasons to reduce the number of data transfers. The synchronize postprocessor is simply a Receiver postprocessor that is set to a value of 1. No applications will transfer anything in to synchronize, so the value of this postprocessor remains always fixed at 1. In addition to the synchronize postprocessor, below are listed other postprocessors used to facilitate the data transfers and output certain quantities of interest.

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [flux_integral]
    # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral<<<{"description": "Computes the integral of the diffusive flux over the specified boundary", "href": "../source/postprocessors/SideDiffusiveFluxIntegral.html"}>>>
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation. This must be provided if the variable is of finite element type"}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable which this postprocessor integrates"}>>> = T
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '10'
  []
  [synchronize]
    type = Receiver<<<{"description": "Reports the value stored in this processor, which is usually filled in by another object. The Receiver does not compute its own value.", "href": "../source/postprocessors/Receiver.html"}>>>
    default<<<{"description": "The default value"}>>> = 1
  []
[]

To understand the purpose of this (optional) transfer, we need to describe in more detail the data transfers that occur when sub-cycling. Please note that this is an advanced feature added for very large runs to squeeze out as much performance as possible - this feature is not necessary for beginner users.

Consider the case where the main application has a time step of 1, but NekRS has a time step of 0.2. After the solution of the main application, the heat flux transfer into NekRS consists of several steps:

Transfer from flux in the main application to the heat_flux receiver variable in the MOOSE-wrapped NekRS app. This is the transfer that happens in the Transfers block.
Once the heat flux is available in the heat_flux variable in the nek.i input, transfer that heat flux into NekRS on the host (i.e. the CPU) by interpolating from the NekRSMesh to the GLL points. Also normalize the heat flux using the heat_flux_integral postprocesor to ensure conservation.
Once the heat flux has been normalized on the host, it is then copied from the host to the device (i.e. the parallel backend, which will be either a CPU or GPU).

If NekRS is run with a much smaller time step than the main application, steps 2 and 3 can be omitted to save on the interpolation from the NekRSMesh to NekRS's GLL points and on the copy from the host to the device. However, MOOSE's design means that the sub-application doesn't really know anything about how it fits into the hierarchical multiapp tree - it is agnostic. So, the user of this postprocessor (plus some settings in NekRSProblem, to be discussed shortly) can be used to only perform steps 2 and 3 only on the synchronization points between NekRS and MOOSE. In other words, if NekRS runs with a time step 100 times smaller than a main application, this feature reduces the mesh interpolation and host-to-device copying by a factor of 100. By transferring this "dummy" postprocessor to the NekRS wrapping, NekRS will have a signal of when the synchronization points occur.

Finally, we specify an executioner and an exodus output for the solid solution.

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
[]

Fluid Input Files

The fluid phase is solved with NekRS, and is specified in the nek.i file. For CHT coupling, first we construct a mirror of NekRS's mesh on the boundaries of interest - the IDs associated with the fluid-solid interfaces (as known to NekRS) are boundaries 1 and 4.

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]
  type = NekRSMesh
  boundary = '1 4'
  volume = true
[]

Next, NekRSProblem is used to describe all aspects of the NekRS wrapping.

[Problem<<<{"href": "../syntax/Problem/index.html"}>>>]
  type = NekRSProblem
  casename<<<{"description": "Case name for the NekRS input files; this is <case> in <case>.par, <case>.udf, <case>.oudf, and <case>.re2."}>>> = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers<<<{"href": "../syntax/Problem/FieldTransfers/index.html"}>>>]
    [heat_flux]
      type = NekBoundaryFlux<<<{"description": "Reads/writes boundary flux data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = to_nek
      usrwrk_slot<<<{"description": "When 'direction = to_nek', the slot(s) in the usrwrk array to write the incoming data; provide one entry for each quantity being passed"}>>> = 0
    []
    [temperature]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
  []
[]

We use synchronization_interval = parent_app to indicate that we want to transfer data into NekRS's .oudf backend only when new coupling data is available from the parent application. When this option is used, NekRSProblem automatically adds a Receiver postprocessor named transfer_in, as if the following were added to the input file:

[Postprocessors]
  [transfer_in]
    type = Receiver
  []
[]

The transfer_in postprocessor simply receives the synchronize postprocessor from the main application, as shown in the MultiAppPostprocessorTransfer in the solid input file. We also add two FieldTransfers. The NekBoundaryFlux will read from an auxiliary variable named heat_flux (automatically created by Cardinal) and normalize according to a postprocessor named heat_flux_integral (also automatically created by Cardinal). The NekFieldVariable will then read from the field variable temperature internal to NekRS and write it into an auxiliary variable (automatically created by Cardinal) named temperature.

We specify a number of other postprocessors in order to query the NekRS solution for each time step.

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral<<<{"description": "Heat flux over a boundary in the NekRS mesh", "href": "../source/postprocessors/NekHeatFluxIntegral.html"}>>>
    boundary<<<{"description": "Boundary ID(s) for which to compute the postprocessor"}>>> = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral<<<{"description": "Heat flux over a boundary in the NekRS mesh", "href": "../source/postprocessors/NekHeatFluxIntegral.html"}>>>
    boundary<<<{"description": "Boundary ID(s) for which to compute the postprocessor"}>>> = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue<<<{"description": "Extreme value (max/min) of a field over the NekRS mesh", "href": "../source/postprocessors/NekVolumeExtremeValue.html"}>>>
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    value_type<<<{"description": "Whether to give the maximum or minimum extreme value"}>>> = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue<<<{"description": "Extreme value (max/min) of a field over the NekRS mesh", "href": "../source/postprocessors/NekVolumeExtremeValue.html"}>>>
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    value_type<<<{"description": "Whether to give the maximum or minimum extreme value"}>>> = min
  []
[]

Finally, we specify a Transient executioner and NekTimeStepper in order for NekRS to choose its time step (subject to any synchronization points specified by the main application). We also specify an Exodus output file format.

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Transient

  [TimeStepper<<<{"href": "../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = NekTimeStepper
  []
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval<<<{"description": "The interval (number of time steps) at which output occurs"}>>> = ${interval}
[]

Additional files necessary to set up the NekRS problem are the same files you'd need to set up a standalone NekRS simulation -

sfr_7pin.re2: NekRS mesh
sfr_7pin.par: High-level settings for the solver, boundary condition mappings to sidesets, and the equations to solve
sfr_7pin.udf: User-defined C++ functions for on-line postprocessing and model setup
sfr_7pin.oudf: User-defined OCCA kernels for boundary conditions and source terms

Begin with the sfr_7pin.par file.

[GENERAL]
  stopAt = numSteps
  numSteps = 1000
  dt = 5.0e-4
  timeStepper = tombo2
  writeControl = steps
  writeInterval = 1000
  polynomialOrder = 3

[MESH]
  file=fluid.re2

[VELOCITY]
  viscosity = 2.37e-4
  density = 834.5
  boundaryTypeMap = W, v, O, W
  residualTol = 1.0e-6

[PRESSURE]
  residualTol = 1.0e-6

[TEMPERATURE]
  conductivity = 64.21
  rhoCp = 1024766.0
  boundaryTypeMap = f, t, O, f
  residualTol = 1.0e-5

Boundaries 1 and 4 will receive heat flux from MOOSE, so these two boundaries are set to flux boundaries, or f for the [TEMPERATURE] block. Other settings are largely the same.

The assignment of boundary condition values is performed in the sfr_7pin.oudf file, shown below. Note that for boundaries 1 and 4, where we want to receive heat flux from MOOSE, we set the value of the flux equal to bc->usrwrk[bc->idM], or the scratch array that is written by NekRSProblem.

void velocityDirichletConditions(bcData * bc)
{
  bc->u = 0.0; // x-velocity
  bc->v = 0.0; // y-velocity
  bc->w = Vz;  // z-velocity
}

void scalarDirichletConditions(bcData * bc)
{
  bc->s = inlet_T;
}

void scalarNeumannConditions(bcData * bc)
{
  // note: when running with Cardinal, Cardinal will allocate the usrwrk
  // array. If running with NekRS standalone (e.g. nrsmpi), you need to
  // replace the usrwrk with some other value or allocate it youself from
  // the udf and populate it with values.
  bc->flux = bc->usrwrk[bc->idM];
}

Finally, the sfr_7pin.udf file contains C++ functions to set up boundary conditions and perform other post-processing operations. In UDF_Setup, we set initial conditions for velocity, pressure, and temperature. For convenience, we define local functions like mass_flowrate() to be able to set problem parameters in a single place and use them multiple places (these functions are not NekRS syntax - i.e. we could equivalently have done something like #define mdot 0.1).

#include "udf.hpp"

float mass_flowrate()
{
  return 0.1;
}

float inlet_temp()
{
  return 355 + 273.15;
}

float inlet_velocity()
{
  setupAide & options = platform->options;

  // flow area (comes from Cubit area measurement)
  float flow_area = 0.000245;

  // get density from input file
  float rho;
  options.getArgs("DENSITY", rho);

  return mass_flowrate() / flow_area / rho;
}

void UDF_LoadKernels(occa::properties & kernelInfo)
{
  // inlet axial velocity (assuming zero radial and azimuthal components)
  kernelInfo["defines/Vz"] = inlet_velocity();

  // inlet temperature
  kernelInfo["defines/inlet_T"] = inlet_temp();
}

void UDF_Setup(nrs_t *nrs)
{
  // set initial conditions for the velocity, temperature, and pressure
  mesh_t * mesh = nrs->cds->mesh[0];

  float inlet_vel = inlet_velocity();

  // loop over all the GLL points and assign directly to the solution arrays by
  // indexing according to the field offset necessary to hold the data for each
  // solution component
  int n_gll_points = mesh->Np * mesh->Nelements;
  for (int n = 0; n < n_gll_points; ++n)
  {
    nrs->U[n + 0 * nrs->fieldOffset] = 0.0;
    nrs->U[n + 1 * nrs->fieldOffset] = 0.0;
    nrs->U[n + 2 * nrs->fieldOffset] = inlet_vel;

    nrs->P[n] = 0.0;

    nrs->cds->S[n + 0 * nrs->cds->fieldOffset[0]] = inlet_temp();
  }
}

Execution and Postprocessing

To run the pseudo-steady model,


mpiexec -np 4 cardinal-opt -i solid.i

Because we used synchronization_interval = parent_app, you will see in the screen output that the data transfers into NekRS only occur on synchronization points with the main application - all other time steps will omit the messages about normalizing heat flux and extracting temperatures from NekRS.

After converting the NekRS output files to a format viewable in Paraview (see instructions here), the simulation results can be displayed. Figure 3 shows the fluid temperature along with the solid mesh; and the solid temperature along with the fluid mesh. The temperature color scale is the same in both figures.

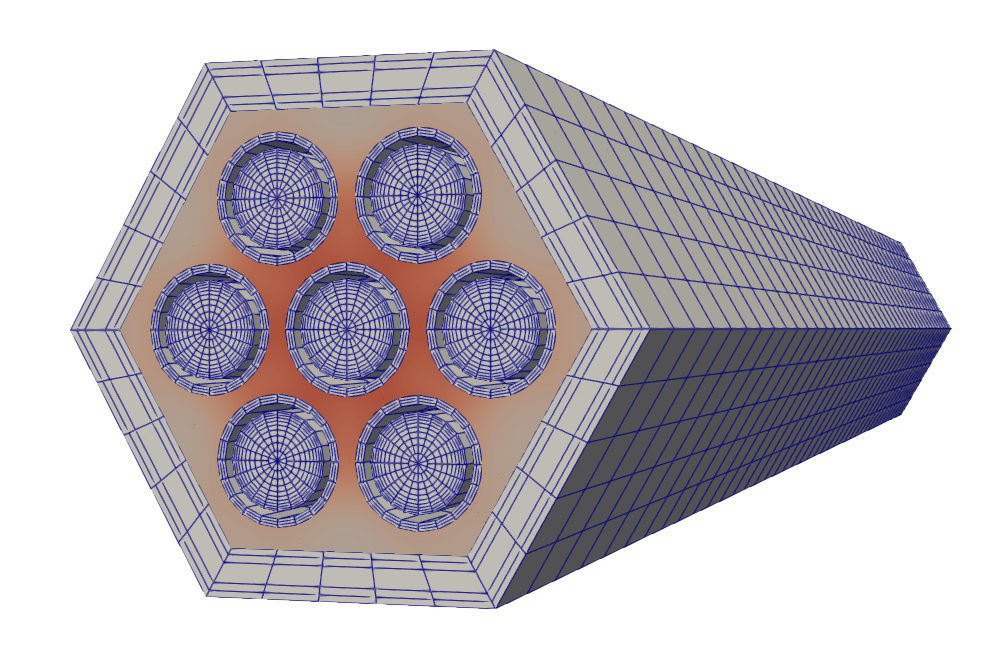
Figure 3: Left: Fluid temperature computed by NekRS for CHT coupling for a bare 7-pin SFR bundle with solid mesh lines shown in blue. Right: Solid temperature computed by MOOSE for CHT coupling for a bare 7-pin SFR bundle with fluid mesh lines shown in blue.

Preserving Flux on Individual Sidesets

By default, NekBoundaryFlux will lump all "receiving" sidesets in NekRS together for the purpose of normalization. For this example, this means that the pin outer surface flux will not exactly match the pin outer flux from MOOSE (and similarly for the duct inner surface flux), because these surfaces are lumped together. In this section, we illustrate a more advanced option to individually preserve flux by sideset.

The input files we will use are the solid_vpp.i and nek_vpp.i files. These files are almost identical to the files described in the previous section, so we only emphasize the differences. First, in the solid model we need to set up individual postprocessors for the heat flux corresponding to each NekRS boundary. Then, we need to set up a VectorOfPostprocessors to fill a vector with each flux postprocessor. Note that the order of the postprocessors must match the boundaries they get mapped to in NekRSMesh.

[VectorPostprocessors<<<{"href": "../syntax/VectorPostprocessors/index.html"}>>>]
  [flux]
    type = VectorOfPostprocessors<<<{"description": "Outputs the values of an arbitrary user-specified set of postprocessors as a vector in the order specified by the user", "href": "../source/vectorpostprocessors/VectorOfPostprocessors.html"}>>>
    postprocessors<<<{"description": "The postprocessors whose values are to be reported"}>>> = 'pin_flux duct_flux'
  []
[]

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [pin_flux]
    type = SideDiffusiveFluxIntegral<<<{"description": "Computes the integral of the diffusive flux over the specified boundary", "href": "../source/postprocessors/SideDiffusiveFluxIntegral.html"}>>>
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation. This must be provided if the variable is of finite element type"}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable which this postprocessor integrates"}>>> = T
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '5'
  []
  [duct_flux]
    type = SideDiffusiveFluxIntegral<<<{"description": "Computes the integral of the diffusive flux over the specified boundary", "href": "../source/postprocessors/SideDiffusiveFluxIntegral.html"}>>>
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation. This must be provided if the variable is of finite element type"}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable which this postprocessor integrates"}>>> = T
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '10'
  []
  [max_fuel_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = T
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = '10'
  []
  [synchronize]
    type = Receiver<<<{"description": "Reports the value stored in this processor, which is usually filled in by another object. The Receiver does not compute its own value.", "href": "../source/postprocessors/Receiver.html"}>>>
    default<<<{"description": "The default value"}>>> = 1
  []
[]

Then, we simply need to replace the MultiAppPostprocessorTransfer with a MultiAppReporterTransfer.

[Transfers<<<{"href": "../syntax/Transfers/index.html"}>>>]
  [nek_temp]
    # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = temperature
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_temp
  []
  [flux]
    # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = flux
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = heat_flux
  []
  [flux_integral_to_nek]
    # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppReporterTransfer<<<{"description": "Transfers reporter data between two applications.", "href": "../source/transfers/MultiAppReporterTransfer.html"}>>>
    to_reporters<<<{"description": "List of the reporter names (object_name/value_name) to transfer the value to."}>>> = 'heat_flux_integral/value'
    from_reporters<<<{"description": "List of the reporter names (object_name/value_name) to transfer the value from."}>>> = 'flux/flux'
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = transfer_in
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = synchronize
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
[]

Finally, we just need to set conserve_flux_by_sideset = true in NekBoundaryFlux in the Nek input file.

[Problem<<<{"href": "../syntax/Problem/index.html"}>>>]
  type = NekRSProblem
  casename<<<{"description": "Case name for the NekRS input files; this is <case> in <case>.par, <case>.udf, <case>.oudf, and <case>.re2."}>>> = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers<<<{"href": "../syntax/Problem/FieldTransfers/index.html"}>>>]
    [heat_flux]
      type = NekBoundaryFlux<<<{"description": "Reads/writes boundary flux data between NekRS and MOOSE."}>>>
      usrwrk_slot<<<{"description": "When 'direction = to_nek', the slot(s) in the usrwrk array to write the incoming data; provide one entry for each quantity being passed"}>>> = 0
      direction<<<{"description": "Direction in which to send data"}>>> = to_nek
      conserve_flux_by_sideset<<<{"description": "Whether to conserve the flux by individual sideset (as opposed to lumping all sidesets together). Setting this option to true requires syntax changes in the input file to use vector postprocessors, and places restrictions on how the sidesets are set up."}>>> = true
    []
    [temperature]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
  []
[]

To run the model,


mpirun -np 4 cardinal-opt -i solid_vpp.i

The physics predictions are nearly identical to those displayed earlier. You will note that when running, Cardinal will print out the heat flux being applied to each individual sideset, instead of lumping them together.


nek0: [boundary 1]: Normalizing NekRS flux of 80710.2 to the conserved MOOSE value of 80336.1
nek0: [boundary 4]: Normalizing NekRS flux of 1995.4 to the conserved MOOSE value of 2006.27
copying solution to nek

Cond. Flux-Conv. Flux Coupling Option

In this section, we modify the CHT boundary conditions to instead compute a convective heat flux with NekRS to apply to MOOSE as a Robin-type boundary condition,

$(3)var element = document.getElementById("moose-equation-465990f0-920e-4282-9641-1e77716f4acd");katex.render(" q''=h(T_w-T_\\infty)", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-da5d589a-ee35-4be0-924a-b003be6d6bf5");katex.render("q''", element, {displayMode:false,throwOnError:false});$ is the heat flux that will be imposed on the solid boundaries, $var element = document.getElementById("moose-equation-2ed1eabd-fc30-4121-8c09-2eb68cff7191");katex.render("h", element, {displayMode:false,throwOnError:false});$ is the convective heat transfer coefficient, $var element = document.getElementById("moose-equation-9c25c0ad-e066-48d0-a7e3-391ecef3f694");katex.render("T_w", element, {displayMode:false,throwOnError:false});$ is NekRS's wall temperature, and $var element = document.getElementById("moose-equation-b38c342d-fbb7-43c2-8082-6136ae517dfa");katex.render("T_\\infty", element, {displayMode:false,throwOnError:false});$ is NekRS's bulk temperature. To use this "Cond. Flux - Conv. Flux" coupling option, we simply need to add user objects to the fluid input files to comput $var element = document.getElementById("moose-equation-7bd0daae-cfff-4f22-882a-a70b6c22761f");katex.render("h", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-ac714dd8-d615-470f-817b-d5aeddb5f0d3");katex.render("T_\\infty", element, {displayMode:false,throwOnError:false});$ . A previous tutorial showed how to compute a heat transfer coefficient with NekRS; we will use this same foundation now to compute $var element = document.getElementById("moose-equation-8c2a3ea0-6a49-40c5-bd15-00d7cf34f741");katex.render("h", element, {displayMode:false,throwOnError:false});$ and then apply this alternative boundary condition to our solid app.

Fluid Input Files

The fluid input files are mostly the same as the case with temperature-flux coupling, so we will only focus on the aspects which are different.

To compute the quantities in Eq. \eqref{eq:hf}, we need to add a few user objects to our Nek wrapping file. We will do so in the nek_fluxflux.i file. For our heat transfer coefficient, we will compute the heat transfer coefficient (ideally as a function of space, since it varies with position and this will yield a more accurate coupling). First, we need to define how NekRS's mesh will be "chunked" for this calculation. We will add a HexagonalSubchannelBin to define the volumetric regions of space in the $var element = document.getElementById("moose-equation-08ae00be-ca55-4e87-b3a4-40bd0810eda0");katex.render("x-y", element, {displayMode:false,throwOnError:false});$ plane and a LayeredBin to define the volumetric regions of space in the axial direction. Together, these binnings are combined to chunk 3-D space.

note

There are an infinite number of ways that you can "chunk" space to compute $var element = document.getElementById("moose-equation-06d23f99-92df-408d-862d-c2283e95f681");katex.render("h", element, {displayMode:false,throwOnError:false});$ , $var element = document.getElementById("moose-equation-9b40b3e7-80f2-4533-afa2-971dae1a58c6");katex.render("T_\\infty", element, {displayMode:false,throwOnError:false});$ , and $var element = document.getElementById("moose-equation-f8ce05e1-18e8-41f3-8866-59dde476ac3c");katex.render("T_\\text{wall}", element, {displayMode:false,throwOnError:false});$ . Our choice in this tutorial simply uses a conventional subchannel-type discretization.

Then, we add additional user objects to compute the necessary terms in Eq. \eqref{eq:hf}:

NekBinnedSideAverage to compute the average heat flux on the pin surfaces (one unique calculation for each axial layer and for each subchannel). The heat flux from MOOSE is written into the zeroth slot in the nrs->usrwrk array, which we indicate as the field we want to average by setting field = usrwrk00.
NekBinnedSideAverage to compute the average wall temperature on the pin surfaces (one unique calculation for each axial layer and for each subchannel). We indicate temperature by setting field = temperature.
NekBinnedVolumeAverage to compute the average bulk temperature over the subchannel volumes (one unique calculation for each axial layer and for each subchannel). We indicate temperature by setting field = temperature.

[UserObjects<<<{"href": "../syntax/UserObjects/index.html"}>>>]
  [axial_bin]
    type = LayeredBin<<<{"description": "Creates a unique spatial bin for layers in a specified direction", "href": "../source/userobjects/LayeredBin.html"}>>>
    direction<<<{"description": "The direction of the layers (x, y, or z)"}>>> = z
    num_layers<<<{"description": "The number of layers between the bounding box of the domain"}>>> = 20
  []
  [volume_bin]
    type = HexagonalSubchannelBin<<<{"description": "Creates a unique spatial bin for each subchannel in a hexagonal lattice", "href": "../source/userobjects/HexagonalSubchannelBin.html"}>>>
    bundle_pitch<<<{"description": "Bundle pitch, or flat-to-flat distance across bundle"}>>> = '${fparse 0.02625*1.1}'
    pin_pitch<<<{"description": "Pin pitch, or distance between pin centers"}>>> = 0.00904000030292588
    pin_diameter<<<{"description": "Pin outer diameter"}>>> = 8e-3
    n_rings<<<{"description": "Number of pin rings, including the centermost pin as a 'ring'"}>>> = 2
  []
  [wall_flux]
    type = NekBinnedSideAverage<<<{"description": "Compute the spatially-binned average of a field over a sideset of the NekRS mesh", "href": "../source/userobjects/NekBinnedSideAverage.html"}>>>
    bins<<<{"description": "Userobjects providing a spatial bin given a point"}>>> = 'axial_bin volume_bin'
    boundary<<<{"description": "Boundary ID(s) over which to compute the bin values"}>>> = '1'
    field<<<{"description": "Field to apply this object to"}>>> = usrwrk00
    map_space_by_qp<<<{"description": "Whether to map the NekRS spatial domain to a bin according to the element centroids (true) or quadrature point locations (false)."}>>> = true
    interval<<<{"description": "Frequency (in number of time steps) with which to execute this user object; user objects can be expensive and not necessary to evaluate on every single time step. NOTE: you probably want to match with 'time_step_interval' in the Output"}>>> = ${interval}
    check_zero_contributions<<<{"description": "Whether to throw an error if no GLL points/element centroids in the NekRS mesh map to a spatial bin; this can be used to ensure that the bins are sufficiently big to get at least one contributing point from the NekRS mesh."}>>> = false
  []
  [wall_temp]
    type = NekBinnedSideAverage<<<{"description": "Compute the spatially-binned average of a field over a sideset of the NekRS mesh", "href": "../source/userobjects/NekBinnedSideAverage.html"}>>>
    bins<<<{"description": "Userobjects providing a spatial bin given a point"}>>> = 'axial_bin volume_bin'
    boundary<<<{"description": "Boundary ID(s) over which to compute the bin values"}>>> = '1'
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    map_space_by_qp<<<{"description": "Whether to map the NekRS spatial domain to a bin according to the element centroids (true) or quadrature point locations (false)."}>>> = true
    interval<<<{"description": "Frequency (in number of time steps) with which to execute this user object; user objects can be expensive and not necessary to evaluate on every single time step. NOTE: you probably want to match with 'time_step_interval' in the Output"}>>> = ${interval}
    check_zero_contributions<<<{"description": "Whether to throw an error if no GLL points/element centroids in the NekRS mesh map to a spatial bin; this can be used to ensure that the bins are sufficiently big to get at least one contributing point from the NekRS mesh."}>>> = false
  []
  [bulk_temp]
    type = NekBinnedVolumeAverage<<<{"description": "Compute the spatially-binned volume average of a field over the NekRS mesh", "href": "../source/userobjects/NekBinnedVolumeAverage.html"}>>>
    bins<<<{"description": "Userobjects providing a spatial bin given a point"}>>> = 'axial_bin volume_bin'
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    map_space_by_qp<<<{"description": "Whether to map the NekRS spatial domain to a bin according to the element centroids (true) or quadrature point locations (false)."}>>> = true
    interval<<<{"description": "Frequency (in number of time steps) with which to execute this user object; user objects can be expensive and not necessary to evaluate on every single time step. NOTE: you probably want to match with 'time_step_interval' in the Output"}>>> = ${interval}
    check_zero_contributions<<<{"description": "Whether to throw an error if no GLL points/element centroids in the NekRS mesh map to a spatial bin; this can be used to ensure that the bins are sufficiently big to get at least one contributing point from the NekRS mesh."}>>> = false
  []
[]

Then, we use these user objects to compute a heat transfer coefficient using HeatTransferCoefficientAux. This heat transfer coefficient will get passed to the solid input file, along the the bulk temperature, for use in the convective flux boundary condition.

Because the boundary condition applied to NekRS is still a conductive heat flux as in Cond. Flux-Temperature CHT Coupling , the case files do not need to be modified.

Solid Input Files

The solid input files are mostly the same as the case with temperature-flux coupling, so we will only focus on the aspects which are different. First, we will use a convective heat flux boundary condition on the pin surfaces (for illustration, we'll leave the Dirichlet temperature condition on the duct inner surface to show that you can mix-and-match as you please).

[BCs<<<{"href": "../syntax/BCs/index.html"}>>>]
  [duct]
    type = MatchedValueBC<<<{"description": "Implements a NodalBC which equates two different Variables' values on a specified boundary.", "href": "../source/bcs/MatchedValueBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    v<<<{"description": "The variable whose value we are to match."}>>> = nek_wall_temp
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '10'
  []
  [pins]
    type = CoupledConvectiveHeatFluxBC<<<{"description": "Convective heat transfer boundary condition with temperature and heat transfer coefficent given by auxiliary variables.", "href": "../source/bcs/CoupledConvectiveHeatFluxBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '5'
    T_infinity<<<{"description": "Field holding far-field temperature"}>>> = nek_bulk_temp
    htc<<<{"description": "Heat transfer coefficient"}>>> = h
  []
  [outer]
    type = ConvectiveHeatFluxBC<<<{"description": "Convective heat transfer boundary condition with temperature and heat transfer coefficent given by material properties.", "href": "../source/bcs/ConvectiveHeatFluxBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = T
    T_infinity<<<{"description": "Material property for far-field temperature"}>>> = 600
    heat_transfer_coefficient<<<{"description": "Material property for heat transfer coefficient"}>>> = 1000
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'duct_outer'
  []
[]

The variables, h and nek_bulk_temp, are fetched from transfers with the NekRS sub-application. The MultiAppGeneralFieldUserObjectTransfer object will directly evaluate the userobject which computed the bulk temperature, at the quadrature points in the solid mesh. The only other new transfer is passing the variable containing the heat transfer coefficient, using a MultiAppGeneralFieldNearestLocationTransfer.

[Transfers<<<{"href": "../syntax/Transfers/index.html"}>>>]
  [nek_bulk_temp]
    # grabs the Nek Tinf and stores it in nek_bulk_temp
    type = MultiAppGeneralFieldUserObjectTransfer<<<{"description": "Transfers user object spatial evaluations from an origin app onto a variable in the target application.", "href": "../source/transfers/MultiAppGeneralFieldUserObjectTransfer.html"}>>>
    source_user_object<<<{"description": "The UserObject you want to transfer values from. It must implement the SpatialValue() class routine"}>>> = bulk_temp
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_bulk_temp
    to_blocks<<<{"description": "Subdomain restriction to transfer to, (defaults to all the target app domain)"}>>> = '1'
  []
  [nek_wall_temp]
    # grabs the Nek wall temperature and stores it in nek_wall_temp
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = temperature
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_wall_temp
    to_boundaries<<<{"description": "The boundary we are transferring to (if not specified, whole domain is used)."}>>> = '5 10'
  []
  [h]
    # grabs the heat transfer coefficient and stores it in h
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = h
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = h
    to_boundaries<<<{"description": "The boundary we are transferring to (if not specified, whole domain is used)."}>>> = '5'
  []
  [flux]
    # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer<<<{"description": "Transfers field data at the MultiApp position by finding the value at the nearest neighbor(s) in the origin application.", "href": "../source/transfers/MultiAppGeneralFieldNearestLocationTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = flux
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = heat_flux
    from_boundaries<<<{"description": "The boundary we are transferring from (if not specified, whole domain is used)."}>>> = '5 10'
  []
  [flux_integral_to_nek]
    # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = heat_flux_integral
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = flux_integral
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = transfer_in
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = synchronize
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
[]

Execution and Postprocessing

To run the pseudo-steady model,


mpiexec -np 4 cardinal-opt -i solid_fluxflux.i

The results are very similar (though not identical) to the flux-temperature coupling case, because we have to chunk up space in order to compute a heat transfer coefficient. This discretization can be faintly seen in Figure 4 (though can be diminished by simply using a finer spatial chunking for the heat transfer coefficient).

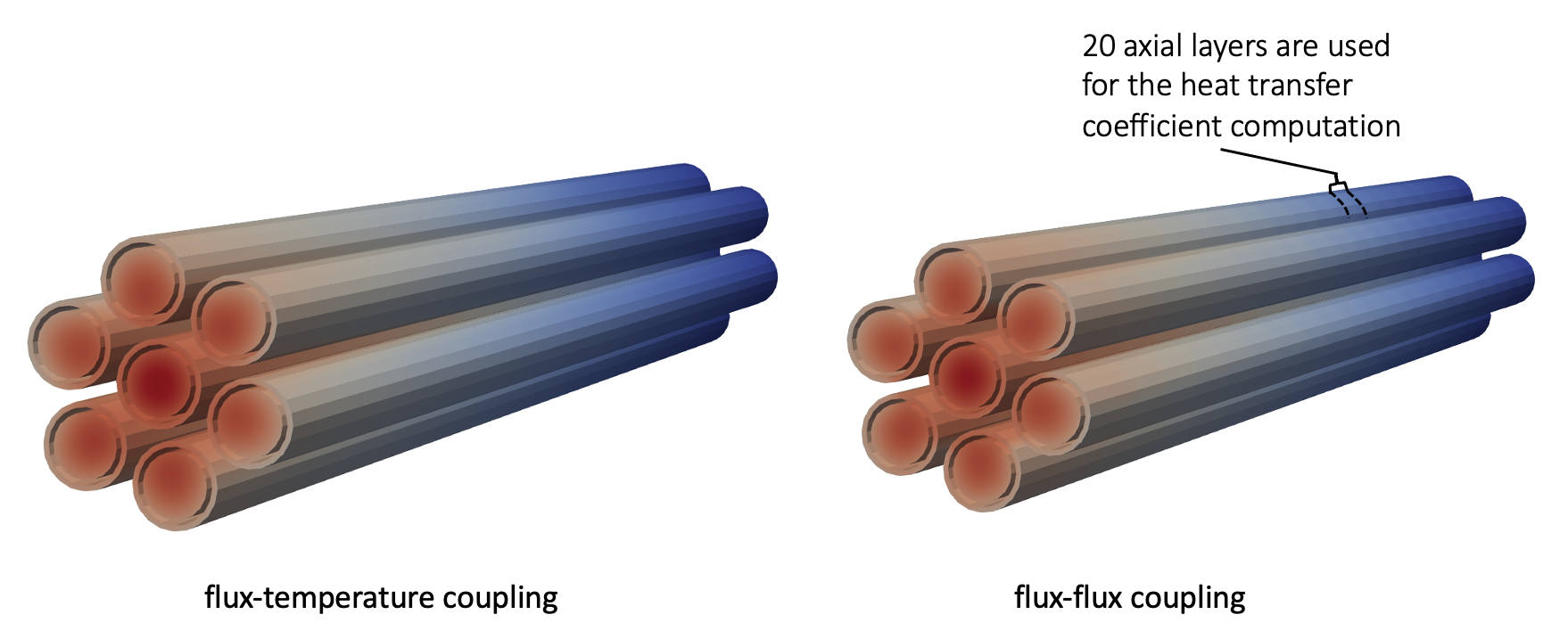
Figure 4: Solid temperature predicted when solving conjugate heat transfer with NekRS using two different CHT boundary conditions.

References

J. Cahalan, L. Deitrich, F. Dunn, D. Fallin, M. Farmer, T. Fanning, T. Kim, L. Krajtl, S. Lomperski, A. Moisseytsev, Y. Momzaki, J. Sienicki, Y. Park, Y. Tang, C. Reed, C. Tzanos, S. Wiedmeyer, W. Yang, and Y. Chikazawa. Advanced Burner Test Reactor Preconceptual Design Report. Technical Report ANL-ABR-1, ANL, 2006.

@techreport{abtr,
    author = "Cahalan, J. and Deitrich, L. and Dunn, F. and Fallin, D. and Farmer, M. and Fanning, T. and Kim, T. and Krajtl, L. and Lomperski, S. and Moisseytsev, A. and Momzaki, Y. and Sienicki, J. and Park, Y. and Tang, Y. and Reed, C. and Tzanos, C. and Wiedmeyer, S. and Yang, W. and Chikazawa, Y.",
    title = "{Advanced Burner Test Reactor Preconceptual Design Report}",
    institution = "ANL",
    year = "2006",
    number = "ANL-ABR-1"
}

(tutorials/sfr_7pin/mesh.i)

[Mesh]

# --- DUCT --- #

  # Make the duct mesh in 2-D; we first create a "solid" hexagon with two blocks
  # so that we can set the inner wall sideset as the boundary between these two blocks,
  # and then delete an inner block to get just the duct walls
  [duct]
    type = PolygonConcentricCircleMeshGenerator
    num_sides = 6
    polygon_size = ${fparse bundle_pitch / 2.0 + duct_thickness}
    num_sectors_per_side = '14 14 14 14 14 14'
    uniform_mesh_on_sides = true

    duct_sizes = '${fparse bundle_pitch / 2.0}'
    duct_block_ids = '10'
    duct_intervals = '4'
    duct_sizes_style = apothem
  []
  [inner_sideset]
    type = SideSetsBetweenSubdomainsGenerator
    input = duct
    new_boundary = '10'
    primary_block = '10'
    paired_block = '1'
  []
  [delete_inside_block]
    type = BlockDeletionGenerator
    input = inner_sideset
    block = '1'
  []

  # rotate the duct by 30 degrees, then add names for sidesets. Delete sideset 1 because
  # we will name some other part of our mesh with sideset 1.
  [rotate]
    type = TransformGenerator
    input = delete_inside_block
    transform = rotate
    vector_value = '30.0 0.0 0.0'
  []
  [rename_sideset_names]
    type = RenameBoundaryGenerator
    input = rotate
    old_boundary = '10000 10'
    new_boundary = 'duct_outer duct_inner'
  []
  [delete_extraneous]
    type = BoundaryDeletionGenerator
    input = rename_sideset_names
    boundary_names = '1'
  []

# --- CLAD --- #

  [clad]
    type = AnnularMeshGenerator
    nr = 3
    nt = 20
    rmin = ${fparse d_pin / 2.0 - t_clad}
    rmax = ${fparse d_pin / 2.0}
    quad_subdomain_id = 1
    tri_subdomain_id = 0
  []
  [rename_clad] # this renames some sidesets on the clad to avoid name clashes
    type = RenameBoundaryGenerator
    input = clad
    old_boundary = '1 0' # outer surface, inner surface
    new_boundary = '5 4'
  []
  [rename_clad_names] # this renames some names on the clad to avoid name clashes
    type = RenameBoundaryGenerator
    input = rename_clad
    old_boundary = '5 4' # outer surface, inner surface
    new_boundary = 'clad_outer clad_inner'
  []

# --- FUEL --- #

  [fuel]
    type = AnnularMeshGenerator
    nr = 10
    nt = 20
    rmin = 0
    rmax = ${fparse d_pellet / 2.0}
    quad_subdomain_id = 2
    tri_subdomain_id = 3
    growth_r = -1.2
  []

# --- COMBINE --- #

  [combine] # this combines the fuel and clad together to make one pin
    type = CombinerGenerator
    inputs = 'rename_clad_names fuel'
  []
  [repeat] # this repeats the pincell 7 times to get the 7 pins, and adds the duct
    type = CombinerGenerator
    inputs = 'combine combine combine combine combine combine combine delete_extraneous'
    positions = '+0.00000000 +0.00000000 +0.00000000
                 +0.00452000 +0.00782887 +0.00000000
                 -0.00452000 +0.00782887 +0.00000000
                 -0.00904000 +0.00000000 +0.00000000
                 -0.00452000 -0.00782887 +0.00000000
                 +0.00452000 -0.00782887 +0.00000000
                 +0.00904000 +0.00000000 +0.00000000
                 +0.0        +0.0        +0.0'
  []
  [extrude]
    type = AdvancedExtruderGenerator
    input = repeat
    direction = '0 0 1'
    num_layers = '40'
    heights = '${L}'
  []
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/mesh_settings.py)

nondimensional = False        # whether to generate the mesh in non-dimensional form
pin_diameter = 8e-3           # pin diameter
pin_pitch = 0.00904           # pin pitch
flat_to_flat = 0.02625        # duct inner flat-to-flat
wire_diameter = 0             # wire diameter
wire_pitch = 0                # wire axial pitch
h = 20.32e-2                  # height
n_pins = 7                    # number of pins

e_per_side = 4                # number of elements along each 1/6 of the pin
e_per_bl = 3                  # number of elements in each boundary layer
e_per_pin_background = 3      # number of background elements in pincell
e_per_assembly_background = 3 # number of background elements in assembly
growth_factor = 1.8           # boundary layer growth factor
nl = 30                       # number of axial layers
bl_height = 0.00006           # height of first boundary layer

# If you would like to apply a radius of curvature to the corners of the
# duct, set the following parameters.
#
# corner_radius: radius of curvature of duct corners
# corner_smoothing: Smoothing factors to apply to the corner movement; must match
#                   the length of the e_per_bl + e_per_assembly_background. You may
#                   need to adjust this parameter if the default doesn't work nicely.
corner_radius = 0
corner_smoothing = '1.0 1.0 1.0 0.75 0.25 0.25'

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_and_duct]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5 10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    to_boundaries = '5 10'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/nek.i)

interval = 100

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
  volume = true
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval = ${interval}
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/nek.i)

interval = 100

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
  volume = true
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval = ${interval}
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/nek.i)

interval = 100

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
  volume = true
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval = ${interval}
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/nek.i)

interval = 100

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
  volume = true
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval = ${interval}
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/sfr_7pin.par)

[GENERAL]
  stopAt = numSteps
  numSteps = 1000
  dt = 5.0e-4
  timeStepper = tombo2
  writeControl = steps
  writeInterval = 1000
  polynomialOrder = 3

[MESH]
  file=fluid.re2

[VELOCITY]
  viscosity = 2.37e-4
  density = 834.5
  boundaryTypeMap = W, v, O, W
  residualTol = 1.0e-6

[PRESSURE]
  residualTol = 1.0e-6

[TEMPERATURE]
  conductivity = 64.21
  rhoCp = 1024766.0
  boundaryTypeMap = f, t, O, f
  residualTol = 1.0e-5

(tutorials/sfr_7pin/sfr_7pin.oudf)

void velocityDirichletConditions(bcData * bc)
{
  bc->u = 0.0; // x-velocity
  bc->v = 0.0; // y-velocity
  bc->w = Vz;  // z-velocity
}

void scalarDirichletConditions(bcData * bc)
{
  bc->s = inlet_T;
}

void scalarNeumannConditions(bcData * bc)
{
  // note: when running with Cardinal, Cardinal will allocate the usrwrk
  // array. If running with NekRS standalone (e.g. nrsmpi), you need to
  // replace the usrwrk with some other value or allocate it youself from
  // the udf and populate it with values.
  bc->flux = bc->usrwrk[bc->idM];
}

(tutorials/sfr_7pin/sfr_7pin.udf)

#include "udf.hpp"

float mass_flowrate()
{
  return 0.1;
}

float inlet_temp()
{
  return 355 + 273.15;
}

float inlet_velocity()
{
  setupAide & options = platform->options;

  // flow area (comes from Cubit area measurement)
  float flow_area = 0.000245;

  // get density from input file
  float rho;
  options.getArgs("DENSITY", rho);

  return mass_flowrate() / flow_area / rho;
}

void UDF_LoadKernels(occa::properties & kernelInfo)
{
  // inlet axial velocity (assuming zero radial and azimuthal components)
  kernelInfo["defines/Vz"] = inlet_velocity();

  // inlet temperature
  kernelInfo["defines/inlet_T"] = inlet_temp();
}

void UDF_Setup(nrs_t *nrs)
{
  // set initial conditions for the velocity, temperature, and pressure
  mesh_t * mesh = nrs->cds->mesh[0];

  float inlet_vel = inlet_velocity();

  // loop over all the GLL points and assign directly to the solution arrays by
  // indexing according to the field offset necessary to hold the data for each
  // solution component
  int n_gll_points = mesh->Np * mesh->Nelements;
  for (int n = 0; n < n_gll_points; ++n)
  {
    nrs->U[n + 0 * nrs->fieldOffset] = 0.0;
    nrs->U[n + 1 * nrs->fieldOffset] = 0.0;
    nrs->U[n + 2 * nrs->fieldOffset] = inlet_vel;

    nrs->P[n] = 0.0;

    nrs->cds->S[n + 0 * nrs->cds->fieldOffset[0]] = inlet_temp();
  }
}

(tutorials/sfr_7pin/solid_vpp.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source]
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity_function = k_sodium
    gap_conductivity_function_variable = T

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_outer]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5'
  []
  [duct_inner]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Functions]
  [k_sodium]
    type = ParsedFunction
    expression = '1.1045e2 + -6.5112e-2 * t + 1.5430e-5 * t * t + -2.4617e-9 * t * t * t'
  []
  [k_HT9]
    type = ParsedFunction
    expression = 'if (t < 1030, 17.622 + 2.428e-2 * t - 1.696e-5 * t * t,
                           12.027 + 1.218e-2 * t)'
  []
  [k_U]
    type = ParsedFunction
    expression = 'if (t < 255.4, 16.170,
                            if (t < 1173.2, (5.907e-6 * t * t + 1.591e-2 * t + 11.712),
                                             38.508))'
  []
[]

[Materials]
  [clad_and_duct]
    type = HeatConductionMaterial
    thermal_conductivity_temperature_function = k_HT9
    temp = T
    block = '1 10'
  []
  [pellet]
    type = HeatConductionMaterial
    thermal_conductivity_temperature_function = k_U
    temp = T
    block = '2 3'
  []
[]

[VectorPostprocessors]
  [flux]
    type = VectorOfPostprocessors
    postprocessors = 'pin_flux duct_flux'
  []
[]

[Postprocessors]
  [pin_flux]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5'
  []
  [duct_flux]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek_vpp.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppReporterTransfer
    to_reporters = 'heat_flux_integral/value'
    from_reporters = 'flux/flux'
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]


[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'
  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid_vpp.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 500.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source]
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity_function = k_sodium
    gap_conductivity_function_variable = T

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [pin_outer]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '5'
  []
  [duct_inner]
    type = MatchedValueBC
    variable = T
    v = nek_temp
    boundary = '10'
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Functions]
  [k_sodium]
    type = ParsedFunction
    expression = '1.1045e2 + -6.5112e-2 * t + 1.5430e-5 * t * t + -2.4617e-9 * t * t * t'
  []
  [k_HT9]
    type = ParsedFunction
    expression = 'if (t < 1030, 17.622 + 2.428e-2 * t - 1.696e-5 * t * t,
                           12.027 + 1.218e-2 * t)'
  []
  [k_U]
    type = ParsedFunction
    expression = 'if (t < 255.4, 16.170,
                            if (t < 1173.2, (5.907e-6 * t * t + 1.591e-2 * t + 11.712),
                                             38.508))'
  []
[]

[Materials]
  [clad_and_duct]
    type = HeatConductionMaterial
    thermal_conductivity_temperature_function = k_HT9
    temp = T
    block = '1 10'
  []
  [pellet]
    type = HeatConductionMaterial
    thermal_conductivity_temperature_function = k_U
    temp = T
    block = '2 3'
  []
[]

[VectorPostprocessors]
  [flux]
    type = VectorOfPostprocessors
    postprocessors = 'pin_flux duct_flux'
  []
[]

[Postprocessors]
  [pin_flux]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5'
  []
  [duct_flux]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek_vpp.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp] # grabs temperature from nekRS and stores it in nek_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppReporterTransfer
    to_reporters = 'heat_flux_integral/value'
    from_reporters = 'flux/flux'
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 500.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]


[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'
  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/nek_vpp.i)

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      usrwrk_slot = 0
      direction = to_nek
      conserve_flux_by_sideset = true
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  execute_on = 'final'
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/nek_fluxflux.i)

interval = 100

[Mesh]
  type = NekRSMesh
  boundary = '1 4'
[]

[Problem]
  type = NekRSProblem
  casename = 'sfr_7pin'
  synchronization_interval = parent_app

  [FieldTransfers]
    [heat_flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
  []
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true

  # this will only display the NekRS output every N time steps; postprocessors
  # are still computed on every step, just not output to the console
  time_step_interval = ${interval}
[]

[UserObjects]
  [axial_bin]
    type = LayeredBin
    direction = z
    num_layers = 20
  []
  [volume_bin]
    type = HexagonalSubchannelBin
    bundle_pitch = ${fparse 0.02625*1.1}
    pin_pitch = 0.00904000030292588
    pin_diameter = 8e-3
    n_rings = 2
  []
  [wall_flux]
    type = NekBinnedSideAverage
    bins = 'axial_bin volume_bin'
    boundary = '1'
    field = usrwrk00
    map_space_by_qp = true
    interval = ${interval}
    check_zero_contributions = false
  []
  [wall_temp]
    type = NekBinnedSideAverage
    bins = 'axial_bin volume_bin'
    boundary = '1'
    field = temperature
    map_space_by_qp = true
    interval = ${interval}
    check_zero_contributions = false
  []
  [bulk_temp]
    type = NekBinnedVolumeAverage
    bins = 'axial_bin volume_bin'
    field = temperature
    map_space_by_qp = true
    interval = ${interval}
    check_zero_contributions = false
  []
[]

[AuxVariables]
  [h]
  []
[]

[AuxKernels]
  [h]
    type = HeatTransferCoefficientAux
    variable = h
    wall_T = wall_temp
    bulk_T = bulk_temp
    heat_flux = wall_flux
  []
[]

[Postprocessors]
  [pin_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '1'
  []
  [duct_flux_in_nek]
    type = NekHeatFluxIntegral
    boundary = '4'
  []
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
[]

(tutorials/sfr_7pin/solid_fluxflux.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 1000.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [duct]
    type = MatchedValueBC
    variable = T
    v = nek_wall_temp
    boundary = '10'
  []
  [pins]
    type = CoupledConvectiveHeatFluxBC
    variable = T
    boundary = '5'
    T_infinity = nek_bulk_temp
    htc = h
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek_fluxflux.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_bulk_temp] # grabs the Nek Tinf and stores it in nek_bulk_temp
    type = MultiAppGeneralFieldUserObjectTransfer
    source_user_object = bulk_temp
    from_multi_app = nek
    variable = nek_bulk_temp
    to_blocks = '1'
  []
  [nek_wall_temp] # grabs the Nek wall temperature and stores it in nek_wall_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_wall_temp
    to_boundaries = '5 10'
  []
  [h] # grabs the heat transfer coefficient and stores it in h
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = h
    from_multi_app = nek
    variable = h
    to_boundaries = '5'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_wall_temp]
    initial_condition = 500.0
  []
  [nek_bulk_temp]
    initial_condition = 400.0
  []
  [h]
    initial_condition = 1000
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

(tutorials/sfr_7pin/solid_fluxflux.i)

d_pellet = 0.603e-2                           # pellet diameter (m)
d_pin = 8.0e-3                                # pin (clad) diameter (m)
t_clad = 0.52e-3                              # clad thickness (m)
L = 20.32e-2                                  # height (m)
bundle_pitch = 0.02625                        # flat-to-flat distance inside the duct (m)
duct_thickness = 0.004                        # duct thickness (m)
pin_power = 10e3                              # bundle power (kW)

!include mesh.i

[GlobalParams]
  search_value_conflicts = false
[]

[Variables]
  [T]
    initial_condition = 1000.0
  []
[]

[Kernels]
  [diffusion]
    type = HeatConduction
    variable = T
  []
  [source] # the "units" of a kernel in the heat equation are W/m^3, so we need to divide the power by the pellet volumes
    type = BodyForce
    variable = T
    function = ${fparse pin_power / (pi * (d_pellet * d_pellet / 4.0) * L)}
    block = '2 3'
  []
[]

[ThermalContact]
  # This adds boundary conditions bewteen the fuel and the cladding, which represents
  # the heat flux in both directions as
  # q''= h * (T_1 - T_2)
  # where h is a conductance that accounts for conduction through a material and
  # radiation between two infinite parallel plate gray bodies.
  [one_to_two]
    type = GapHeatTransfer
    variable = T
    primary = '1'
    secondary = '4'

    # we will use a quadrature-based approach to find the gap width and cross-side temperature
    quadrature = true

    # emissivity of the fuel
    emissivity_primary = 0.8

    # emissivity of the clad
    emissivity_secondary = 0.8

    # thermal conductivity of the gap material
    gap_conductivity = 60.0

    # geometric terms related to the gap
    gap_geometry_type = CYLINDER
    cylinder_axis_point_1 = '0 0 0'
    cylinder_axis_point_2 = '0 0 ${L}'
  []
[]

[BCs]
  [duct]
    type = MatchedValueBC
    variable = T
    v = nek_wall_temp
    boundary = '10'
  []
  [pins]
    type = CoupledConvectiveHeatFluxBC
    variable = T
    boundary = '5'
    T_infinity = nek_bulk_temp
    htc = h
  []
  [outer]
    type = ConvectiveHeatFluxBC
    variable = T
    T_infinity = 600
    heat_transfer_coefficient = 1000
    boundary = 'duct_outer'
  []
[]

[Materials]
  [clad_and_duct]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '26'
    block = '1 10'
  []
  [pellet]
    type = GenericConstantMaterial
    prop_names = 'thermal_conductivity'
    prop_values = '23'
    block = '2 3'
  []
[]

[Postprocessors]
  [flux_integral] # evaluate the total heat flux for normalization
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = T
    boundary = '5 10'
  []
  [max_fuel_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '2 3'
  []
  [max_clad_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '1'
  []
  [max_duct_T]
    type = NodalExtremeValue
    variable = T
    value_type = max
    block = '10'
  []
  [synchronize]
    type = Receiver
    default = 1
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek_fluxflux.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_bulk_temp] # grabs the Nek Tinf and stores it in nek_bulk_temp
    type = MultiAppGeneralFieldUserObjectTransfer
    source_user_object = bulk_temp
    from_multi_app = nek
    variable = nek_bulk_temp
    to_blocks = '1'
  []
  [nek_wall_temp] # grabs the Nek wall temperature and stores it in nek_wall_temp
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_wall_temp
    to_boundaries = '5 10'
  []
  [h] # grabs the heat transfer coefficient and stores it in h
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = h
    from_multi_app = nek
    variable = h
    to_boundaries = '5'
  []
  [flux] # sends heat flux in flux to nekRS
    type = MultiAppGeneralFieldNearestLocationTransfer
    source_variable = flux
    to_multi_app = nek
    variable = heat_flux
    from_boundaries = '5 10'
  []
  [flux_integral_to_nek] # sends the heat flux integral (for normalization) to nekRS
    type = MultiAppPostprocessorTransfer
    to_postprocessor = heat_flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

[AuxVariables]
  [nek_wall_temp]
    initial_condition = 500.0
  []
  [nek_bulk_temp]
    initial_condition = 400.0
  []
  [h]
    initial_condition = 1000
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
    block = '1 10'
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = T
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '5 10'
  []
[]

[Executioner]
  type = Transient
  dt = 5e-2
  nl_abs_tol = 1e-5
  nl_rel_tol = 1e-16
  petsc_options_value = 'hypre boomeramg'
  petsc_options_iname = '-pc_type -pc_hypre_type'

  steady_state_detection = true
  steady_state_tolerance = 1e-2
[]

[Outputs]
  exodus = true
[]

Geometry and Computational Model
Meshing
Cond . Flux - Temperature CHT Coupling
Execution and Postprocessing
Cond . Flux - Conv . Flux Coupling Option
References