Comparison of surrogates using a time-dependent problem

This example is meant to demonstrate how non-intrusive surrogate models can be generated for time-dependent problems. Nearest Point, Polynomial Regression and Polynomial Chaos Expansion Surrogates are compared on a non-linear diffusion problem with an oscillating source.

Overview

In this case, a time-dependent nonlinear diffusion problem is solved on a square with an oscillating source in the center. The geometry is presented in Figure 1. It consists of a Ω=[−0.5,0.5]×[−0.5,0.5]\Omega = [-0.5, 0.5]\times [-0.5, 0.5] square with a Ωs=[−0.1,0.1]×[−0.1,0.1]\Omega_s = [-0.1, 0.1]\times [-0.1, 0.1] source region in the center. The boundaries of the problem are denoted by Γ\Gamma. The strong formulation of the problem is:

∂T∂t−∇⋅(C[300T]2∇T)=1000sin⁡(f t)γ(r),r∈Ω\frac{\partial T}{\partial t} - \nabla\cdot\left(C \left[\frac{300}{T}\right]^2\nabla T\right) = 1000\sin(f~ t)\gamma(\textbf{r}), \quad \textbf{r}\in \Omega(1)−C[300T]2∇T⋅n=0,r∈Γ- C \left[\frac{300}{T}\right]^2\nabla T \cdot \textbf{n} = 0, \quad \textbf{r} \in \Gamma(2)

where TT is temperature, and γ(r)\gamma(\textbf{r}) is a selection function returning 1 when r∈Ωs\textbf{r}\in\Omega_s and 0 otherwise. Parameters C1C_1 and ff influence the magnitude of the diffusion coefficient and the oscillation frequency of the source. Furthermore, it is assumed that the system is initially (at t=0t=0) at constant temperature, T0T_0. The uncertain parameters in the this problem are CC, ff and T0T_0. A reference solution for the first 1 s1~s of the transient is presented in Figure 2.

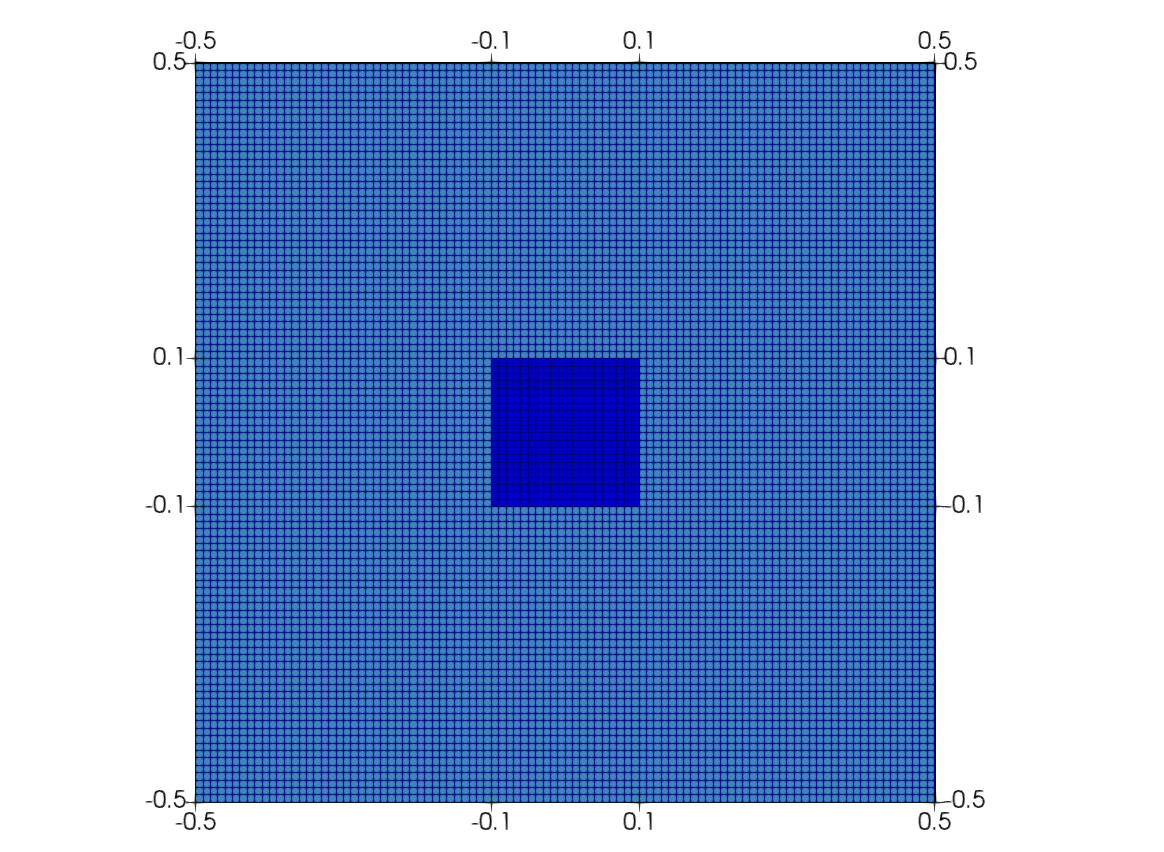
Figure 1: The geometry of the problem.

Figure 2: Reference solution for the problem.

In this problem the Quantities of Interest (QoIs) are the minimum and maximum temperatures in the domain over the fist 1 s1~s of the transient:

Tmax⁡=max⁡r∈Ω, t∈[0,1]T(r,t),andTmin⁡=min⁡r∈Ω, t∈[0,1]T(r,t).\begin{aligned}\\ T_{\max} &= \max_{\textbf{r}\in\Omega,~t\in[0,1]}T(\textbf{r},t),& \text{and} \quad T_{\min} &= \min_{\textbf{r}\in\Omega,~t\in[0,1]}T(\textbf{r},t). \end{aligned}(3)

The uncertain parameters are assumed to be uniformly distributed ∼U(a,b)\sim\mathcal{U}(a, b) between their corresponding minimum (aa) and maximum (bb) values:

ParameterSymbolDistribution
Diffusion coefficient multiplierCC∼U(0.01,0,02)\sim\mathcal{U}(0.01, 0,02)
Frequency multiplierff∼U(15,25)\sim\mathcal{U}(15, 25)
Initial temperatureT0T_0∼U(270,330)\sim\mathcal{U}(270, 330)

Solving the problem without uncertain parameters

The first step towards creating surrogate models is the generation of a full-order model which can solve Eq. (1) with fixed parameter combinations. The complete input file for this case is presented in Listing 1. It is visible that a 100×100100\times 100 mesh and Δt=0.01 s\Delta t = 0.01~s timestep is used to solve the transient problem.

Listing 1: Complete input file for the time-dependent heat equation problem in this study.

[Functions]
  [src_func]
    type = ParsedFunction
    expression = "1000*sin(f*t)"
    symbol_names = 'f'
    symbol_values = '20'
  []
[]

[Mesh]
  [msh]
    type = GeneratedMeshGenerator
    dim = 2
    nx = 100
    xmin = -0.5
    xmax = 0.5
    ny = 100
    ymin = -0.5
    ymax = 0.5
  []
  [source_domain]
    type = ParsedSubdomainMeshGenerator
    input = msh
    combinatorial_geometry = '(x<0.1 & x>-0.1) & (y<0.1 & y>-0.1)'
    block_id=1
  []
[]

[Variables]
  [T]
    initial_condition = 300
  []
[]

[Kernels]
  [diffusion]
    type = MatDiffusion
    variable = T
    diffusivity = diff_coeff
  []
  [source]
    type = BodyForce
    variable = T
    function = src_func
    block = 1
  []
  [time_deriv]
    type = TimeDerivative
    variable = T
  []
[]

[Materials]
  [diff_coeff]
    type = ParsedMaterial
    property_name = diff_coeff
    coupled_variables = 'T'
    constant_names = 'C'
    constant_expressions = 0.02
    expression = 'C * pow(300/T, 2)'
  []
[]

[BCs]
  [neumann_all]
    type = NeumannBC
    variable = T
    boundary = 'left right top bottom'
    value = 0
  []
[]

[Executioner]
  type = Transient
  num_steps = 100
  dt = 0.01
  solve_type = PJFNK
  petsc_options_iname = '-pc_type -pc_hypre_type'
  petsc_options_value = 'hypre boomeramg'
  nl_rel_tol = 1e-6
  l_abs_tol = 1e-6
  timestep_tolerance = 1e-6
[]

[Postprocessors]
  [max]
    type = NodalExtremeValue
    variable = T
  []
  [min]
    type = NodalExtremeValue
    variable = T
    value_type = min
  []
  [time_max]
    type = TimeExtremeValue
    postprocessor = max
  []
  [time_min]
    type = TimeExtremeValue
    postprocessor = min
    value_type = min
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_sub.i)

Training surrogate models

This problem involves the generation of three surrogates: a NearestPointSurrogate, a PolynomialRegressionSurrogate and a PolynomialChaos. All three of them are constructed using multiple instances of the full-order problem as sub-applications. This step is managed by a trainer input file which is responsible for creating parameter samples, transferring those to sub-applications and collecting the corresponding results. The reader is recommended to read Training a Surrogate Model and Parameter Study to get a clear picture on how to train and set up a surrogate model.

The training phase starts with the definition of the distributions for the uncertain parameters in the Distributions block. The uniform distributions can be defined as:

[Distributions]
  [C_dist]
    type = Uniform
    lower_bound = 0.01
    upper_bound = 0.02
  []
  [f_dist]
    type = Uniform
    lower_bound = 15
    upper_bound = 25
  []
  [init_dist]
    type = Uniform
    lower_bound = 270
    upper_bound = 330
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_trainer.i)

Next, multiple parameter vectors are prepared by sampling the underlying distributions using the objects in the Samplers block. In this case, the samples are generated by a QuadratureSampler, which is optimal for the polynomial chaos expansion. Since the execution of this example is expensive in terms of computation time, the same samples are used to train the other surrogates as well. It is not visible, but the sampler prepares 216 parameter vectors altogether.

[Samplers]
  [sample]
    type = Quadrature
    order = 5
    distributions = 'C_dist f_dist init_dist'
    execute_on = PRE_MULTIAPP_SETUP
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_trainer.i)

The objects in blocks Controls, MultiApps, Transfers and Reporters are responsible for managing the communication between the trainer and sub-applications, execution of the sub-applications and the collection of the results. For a more detailed description of these blocks see Parameter Study and Training a Surrogate Model.

[MultiApps]
  [runner]
    type = SamplerFullSolveMultiApp
    input_files = 'trans_diff_sub.i'
    sampler = sample
  []
[]

[Controls]
  [cmdline]
    type = MultiAppSamplerControl
    multi_app = runner
    sampler = sample
    param_names = 'Materials/diff_coeff/constant_expressions Functions/src_func/vals Variables/T/initial_condition'
  []
[]

[Transfers]
  [results]
    type = SamplerReporterTransfer
    from_multi_app = runner
    sampler = sample
    stochastic_reporter = trainer_results
    from_reporter = 'time_max/value time_min/value'
  []
[]

[Reporters]
  [trainer_results]
    type = StochasticReporter
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_trainer.i)

Next, six trainers (three different surrogates for each QoI) are defined in the Trainers block. These objects use the data from Samplers and Reporters. A polynomial chaos surrogate of order 5, a polynomial regression surrogate with a polynomial of degree at most 4 and a nearest point surrogate is used for both QoIs in this work. The PolynomialChaosTrainer also needs knowledge about the underlying parameter distributions to be able to select appropriate polynomials.

[Trainers]
  [pc_max]
    type = PolynomialChaosTrainer
    execute_on = final
    order = 5
    distributions = 'C_dist f_dist init_dist'
    sampler = sample
    response = trainer_results/results:time_max:value
  []
  [pc_min]
    type = PolynomialChaosTrainer
    execute_on = final
    order = 5
    distributions = 'C_dist f_dist init_dist'
    sampler = sample
    response = trainer_results/results:time_min:value
  []
  [np_max]
    type = NearestPointTrainer
    execute_on = final
    sampler = sample
    response = trainer_results/results:time_max:value
  []
  [np_min]
    type = NearestPointTrainer
    execute_on = final
    sampler = sample
    response = trainer_results/results:time_min:value
  []
  [pr_max]
    type = PolynomialRegressionTrainer
    regression_type = "ols"
    execute_on = final
    max_degree = 4
    sampler = sample
    response = trainer_results/results:time_max:value
  []
  [pr_min]
    type = PolynomialRegressionTrainer
    regression_type = "ols"
    execute_on = final
    max_degree = 4
    sampler = sample
    response = trainer_results/results:time_min:value
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_trainer.i)

As a last step in the training process, the important parameters of the trained surrogates are saved into restartable data files, which can be used to construct the surrogate models again without repeating the training process.

[Outputs]
  [out]
    type = SurrogateTrainerOutput
    trainers = 'pc_max pc_min np_max np_min pr_max pr_min'
    execute_on = FINAL
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_trainer.i)

Evaluation of surrogate models

A new main input file has been created to evaluate the surrogate models. This input file uses the same parameter distribution as the one used for the training of the surrogates. Each surrogate model is tested using a new, test parameter sample set, which is generated using a LatinHypercube object in the Samplers block. Since the surrogate models are orders of magnitude faster, 100,000100,000 samples are prepared for testing (compared to 216216 used for training).

[Samplers]
  [sample]
    type = LatinHypercube
    num_rows = 100000
    distributions = 'C_dist f_dist init_dist'
    execute_on = PRE_MULTIAPP_SETUP
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_surr.i)

Next, the necessary objects are created in the Surrogates block using the information available within the corresponding restartable data files.

[Surrogates]
  [pc_min]
    type = PolynomialChaos
    filename = 'trans_diff_trainer_out_pc_min.rd'
  []
  [pc_max]
    type = PolynomialChaos
    filename = 'trans_diff_trainer_out_pc_max.rd'
  []
  [pr_min]
    type = PolynomialRegressionSurrogate
    filename = 'trans_diff_trainer_out_pr_min.rd'
  []
  [pr_max]
    type = PolynomialRegressionSurrogate
    filename = 'trans_diff_trainer_out_pr_max.rd'
  []
  [np_min]
    type = NearestPointSurrogate
    filename = 'trans_diff_trainer_out_np_min.rd'
  []
  [np_max]
    type = NearestPointSurrogate
    filename = 'trans_diff_trainer_out_np_max.rd'
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_surr.i)

These surrogate models are then evaluated at the points defined in the testing sample batch. This is done using objects in the Reporters block. Furthermore, the mean values and standard deviations of the QoI-s together with the 95%95\% confidence intervals are generated as well.

[Reporters]
  [eval_surr]
    type = EvaluateSurrogate
    model = 'pc_max pc_min pr_max pr_min np_max np_min'
    sampler = sample
    parallel_type = ROOT
  []
  [eval_surr_stats]
    type = StatisticsReporter
    reporters = 'eval_surr/pc_max eval_surr/pc_min eval_surr/pr_max eval_surr/pr_min eval_surr/np_max eval_surr/np_min'
    compute = 'mean stddev'
    ci_method = 'percentile'
    ci_levels = '0.05 0.95'
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/combined/trans_diff_2d/trans_diff_surr.i)

Results and Analysis

In this section the results from the different surrogate models are provided. Additionally, the full-order model has been tested with a 2,000 sample batch to serve as a reference solution. The main input file for testing with the full-order model is available here. A short analysis of the results is provided as well.

First, the distributions of QoI-s from the surrogates are compared to the reference results. The histograms showing the distribution of the maximum temperature through the transient are presented below. The figures can be enlarged by clicking on them.

Figure 3: Polynomial Chaos Expansion Surrogate.

Figure 4: Polynomial Regression Surrogate.

Figure 5: Nearest Point Surrogate.

It is visible that even with 2,000 samples, the reference results still exhibit a high statistical fluctuation. Unfortunately, having considerably more than 2,000 samples using the full-order model is not efficient due to the extremely long simulation time. It is also visible that both the polynomial chaos and polynomial regression surrogates yield approximately the same results, and with 100,000 samples, the distributions are much smoother. On the other hand, the nearest point surrogate introduces additional fluctuations which means that it is not capable of reconstructing the shape of the original distribution at all. The same phenomena is experienced with the minimum temperature. The corresponding histograms are presented below.

Figure 6: Polynomial Chaos Expansion Surrogate.

Figure 7: Polynomial Regression Surrogate.

Figure 8: Nearest Point Surrogate.

Next, the statistical moments are compared in Table 1 for the maximum temperature and in Table 2 for the minimum temperature of the system.

Table 1: The mean and standard deviation of the maximum temperature obtained using the surrogates and a reference full-order model.

ModelNumber of samplesMean95% CIStd. Dev.95% CI
Full-order model (reference)2,000396.74[395.90, 397.58]22.86[22.36, 23.33]
Nearest Point Surrogate100,000396.87[396.74, 396.99]23.57[23.50, 23.64]
Polynomial Chaos Surrogate100,000396.77[396.65, 396.88]22.85[22.78, 22.92]
Polynomial Regression Surrogate100,000396.77[396.65, 396.88]22.85[22.78, 22.93]

Table 2: The mean and standard deviation of the minimum temperature obtained using the surrogates and a reference full-order model.

ModelNumber of samplesMean95% CIStd. Dev.95% CI
Full-order model (reference)2,000260.66[259.94, 261.38]19.30[18.96, 19.64]
Nearest Point Surrogate100,000260.46[260.36, 260.56]19.77[19.72, 19.82]
Polynomial Chaos Surrogate100,000260.46[260.36, 260.56]19.17[19.12, 19.21]
Polynomial Regression Surrogate100,000260.46[260.36, 260.56]19.17[19.12, 19.22]

Even though there are small differences in the mean values, it can be concluded that all three of the surrogates managed to give the correct answer. The differences between the full-order model and surrogates are statistically insignificant. For the standard deviations, on the other hand, only the polynomial chaos and polynomial regression give back the statistically equivalent results. Lastly, the gain in computation time is presented in Table 3. It is important to mention that all of the results have been obtained using 8 cores of a single machine.

Table 3: The wall-clock times of different steps in the surrogate modeling process.

CaseWall-clock time (s)
Creating reference results (2000 samples)16,374.2
Training surrogates1910.4
Evaluating surrogates (without computing CI)1.6
Evaluating surrogates (with computing CI)275.0

It is visible that training and using a surrogate model is beneficial in this case since it saves a considerable amount of computation time. It can also be observed that computing the confidence intervals for surrogate models is the most work intensive step in the testing phase. This is due to the frequent resampling of the results vectors.