Turbulent LES Flow in a Heated Pebble Bed

In this tutorial, you will learn how to:

Couple NekRS to MOOSE for CHT for Large Eddy Simulation (LES) in a pebble bed
Manipulate the NekRS solution on each time step through custom user-defined kernels
Adjust sidesets in the NekRS mesh prior to usage

To access this tutorial,


cd cardinal/tutorials/pebble_67

This tutorial also requires you to download some mesh files from Box. Please download the files from the pebble_67 folder here and place these files within the same directory structure in tutorials/pebble_67.

note:Computing Needs

This tutorial requires HPC resources to run.

Geometry and Computational Model

The geometry consists of a small packed bed with 67 spheres each with diameter of $var element = document.getElementById("moose-equation-38aead65-50f6-4b5e-8d67-3a5800e08801");katex.render("d_p=6", element, {displayMode:false,throwOnError:false});$ cm; helium flows in the space between pebbles. A cut-away through the center of the bed is shown in Figure 1. The pebbles are packed into a cylinder with diameter of $var element = document.getElementById("moose-equation-34498828-f09d-4ced-ab56-6e1ec19b7a4e");katex.render("4.4d_p", element, {displayMode:false,throwOnError:false});$ . 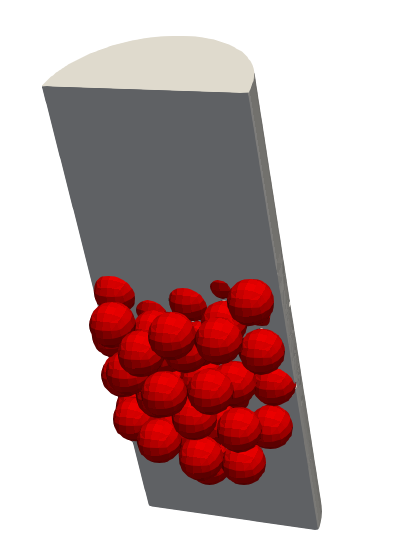The pebbles begin around $var element = document.getElementById("moose-equation-2348a059-5b60-420e-8de5-d652f3ee51ca");katex.render("2.5d_p", element, {displayMode:false,throwOnError:false});$ upstream from the cylinder inlet, and the packed region has a total height of about $var element = document.getElementById("moose-equation-6f67c7a5-7302-45d7-842c-b743be58c7c8");katex.render("5d_p", element, {displayMode:false,throwOnError:false});$ .

Figure 1: Cutaway through the domain in a 67-pebble packed bed. Pebbles are shown in red, while the fluid region is shown in gray.

Table 1 summarizes the geometry and operating conditions of this model. The Reynolds number is based on the pebble diameter.

Table 1: Geometric and boundary condition specifications for a 67-pebble bed

Parameter	Value
Pebble diameter, $var element = document.getElementById("moose-equation-8d35c8e5-729d-4f54-ab42-6b205075c941");katex.render("d_p", element, {displayMode:false,throwOnError:false});$	6 cm
Inlet temperature	523 K
Outlet pressure	4 MPa
Reynolds number	1460
Prandtl number	0.71
Power	24 kW

Heat Conduction Model

The MOOSE heat transfer module is used to solve for energy conservation in the solid, with the time derivative neglected in order to more quickly approach steady state. The solid mesh is shown in Figure 2; the outer surface of the pebbles is sideset 0.

Figure 2: Mesh for the solid heat conduction model

This mesh is generated using MOOSE mesh generators by building a mesh for a single sphere and repeating it 67 times, translated to the position of each pebble. The pebble positions are obtained using off-line discrete element modeling (not discussed here). Note that while chamfers are accounted for in the fluid mesh, that the 67 pebbles are not interconnected to one another for simplicity.

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]
  [sphere]
    type = SphereMeshGenerator<<<{"description": "Generate a 3-D sphere mesh centered on the origin", "href": "../source/meshgenerators/SphereMeshGenerator.html"}>>>
    radius<<<{"description": "Sphere radius"}>>> = 0.03
    nr<<<{"description": "Number of radial elements"}>>> = 2
  []
  [cmbn]
    type = CombinerGenerator<<<{"description": "Combine multiple meshes (or copies of one mesh) together into one (disjoint) mesh.  Can optionally translate those meshes before combining them.", "href": "../source/meshgenerators/CombinerGenerator.html"}>>>
    inputs<<<{"description": "The input MeshGenerators.  This can either be N generators or 1 generator.  If only 1 is given then 'positions' must also be given."}>>> = sphere
    positions_file<<<{"description": "Alternative way to provide the position of each given mesh."}>>> = 'pebble_positions.txt'
  []
[]

The interior of the pebbles is homogenized. We will also assume a uniform power distribution in the pebbles. On the pebble surfaces, a Dirichlet temperature is provided by NekRS. We will run the solid model first, so we must specify an initial condition for the wall temperature, which we simply set to the fluid inlet temperature.

NekRS Model

NekRS solves the incompressible Navier-Stokes equations in non-dimensional form. Turbulence is modeled using LES using a high-pass filter.

The NekRS files are:

pb67.re2: NekRS mesh
pb67.par: High-level settings for the solver, boundary condition mappings to sidesets, and the equations to solve
pb67.udf: User-defined C++ functions for on-line postprocessing and model setup
pb67.oudf: User-defined Open Concurrent Compute Abstraction (OCCA) kernels for boundary conditions, source terms, and other equation manipulations
pb67.usr: Legacy Fortran backend for postprocessing and input modifications

The fluid mesh is shown in Figure 3 using Paraview's "crinkle clip" feature to more clearly delineate individual elements. The pebble locations are shown in red for additional context. This mesh contains 122,284 hexahedral elements. This mesh is generated using a Voronoi cell approach Lan et al. (2021).

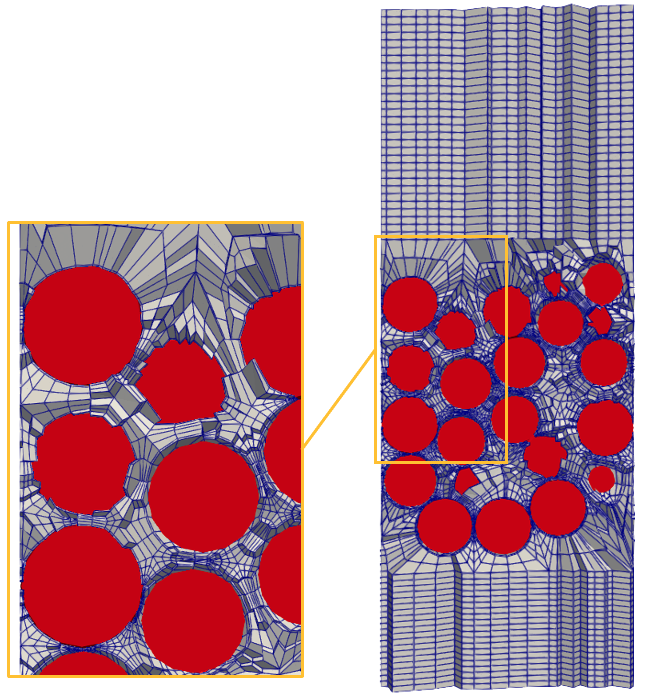
Figure 3: Mesh for the NekRS CFD model; GLL points are not shown

Next, the .par file contains problem setup information. This input solves in non-dimensional form, at a Reynolds number of 1460 and a Peclet number of 1036. Note the LES filter specification in the [GENERAL] block.

[GENERAL]
  polynomialOrder = 7
  stopAt = endTime
  endTime = 500

  dt = 2.0e-05
  timeStepper = tombo2
  subCyclingSteps = 2

  writeControl = steps
  writeInterval = 2000

  filtering = hpfrt
  filterWeight = 0.2/${dt}
  filterModes = 2

[PRESSURE]
  residualTol = 1e-04
  preconditioner = multigrid
  smootherType = chebyshev+jac
  initialGuess = projectionAconj + nVector = 30

[VELOCITY]
  boundaryTypeMap = inlet, outlet, wall, wall
  density = 1.0
  viscosity = -1460.0
  residualTol = 1e-06

[TEMPERATURE]
  boundaryTypeMap = t, I, I, f
  residualTol = 1e-06
  rhoCp = 1.0
  conductivity = -1036.0

In the .oudf file, we define boundary conditions. The inlet boundary is set to a temperature of 0 (a dimensional temperature of $var element = document.getElementById("moose-equation-cc795e4e-4e9b-42b8-89dc-193e98ea9e6b");katex.render("T_{ref}", element, {displayMode:false,throwOnError:false});$ ), while the fluid-solid interface will receive a heat flux from MOOSE. The inlet velocity condition is set to $var element = document.getElementById("moose-equation-14897d33-f62c-4efc-84fa-905feb04aff0");katex.render("V_z=1", element, {displayMode:false,throwOnError:false});$ , with a stabilized outflow for pressure.

void velocityDirichletConditions(bcData *bc)
{
  bc->u = 0.0;
  bc->v = 0.0;
  bc->w = 1.0;
}

// Stabilized outflow (Dong et al)
void pressureDirichletConditions(bcData *bc)
{
  const dfloat iU0delta = 20.0;
  const dfloat un = bc->u*bc->nx + bc->v*bc->ny + bc->w*bc->nz;
  const dfloat s0 = 0.5 * (1.0 - tanh(un*iU0delta));
  bc->p = -0.5 * (bc->u*bc->u + bc->v*bc->v + bc->w*bc->w) * s0;
}

void scalarDirichletConditions(bcData *bc)
{
  bc->s = 0.0;
}

void scalarNeumannConditions(bcData *bc)
{
  // note: when running with Cardinal, Cardinal will allocate the usrwrk
  // array. If running with NekRS standalone (e.g. nrsmpi), you need to
  // replace the usrwrk with some other value or allocate it youself from
  // the udf and populate it with values.
  bc->flux = bc->usrwrk[bc->idM];
}

@kernel void clipTemperature(const dlong Nelements,
                 @restrict dfloat * TEMP)
{

  for (dlong e=0;e<Nelements;++e;@outer(0))
  {
    for (int n=0;n<p_Np;++n;@inner(0))
    {
      const int id = e * p_Np + n;
      const dfloat clip_temperature_max = 100.0;
      const dfloat clip_temperature_min = 0.0;

      if (TEMP[id] > clip_temperature_max)
        TEMP[id] = clip_temperature_max;
      if (TEMP[id] < clip_temperature_min)
        TEMP[id] = clip_temperature_min;
    }
  }
}

@kernel void manipulateOutlet(const dlong Nelements,
                    const dlong uOffset,
                    const dlong sOffset,
                    @restrict const dfloat * TEMP,
                    @restrict dfloat * UPROP,
                    @restrict dfloat * SPROP,
                    @restrict const dfloat * Z)
{
  for (dlong e=0;e<Nelements;++e;@outer(0))
  {
    for (int n=0;n<p_Np;++n;@inner(0))
    {
      const int id = e*p_Np + n;

       // change outlet viscosity/conductivity

      // my current z position
      dfloat local_z = Z[id];

      // height above which I want to manipulate viscosity and conductivity;
      // I will apply a ramping of viscosity between z1 and z2, and set a very
      // high value above z2
      dfloat z1 = 4.6;
      dfloat z2 = 5.0;

      dfloat rho = 1.0;
      dfloat visc = 1.0 / 10000.0;
      dfloat cond = 1.0 / 7100.0;
      dfloat Cp = 1.0;

      // increase viscosity and conductivity near outlet
      dfloat factor = 1.0;
      if (local_z >= z2)
        factor = 101.0;
      else if (local_z > z1 && local_z < z2)
        factor = 1.0 + 100.0 * (local_z - z1) / (z2 - z1);

      visc = factor * visc;
      cond = factor * cond;

      UPROP[id + 0*uOffset] = visc;
      SPROP[id + 0*sOffset] = cond;
      UPROP[id + 1*uOffset] = rho;
      SPROP[id + 1*sOffset] = rho*Cp;
    }
  }
}

We also create two custom kernels which we shall use to manipulate the NekRS solution on each time step:

Clip temperature so that it is always within the range of $var element = document.getElementById("moose-equation-6def22e5-04a0-4609-a7f3-3f9fc285856d");katex.render("0\\leq T^\\dagger\\leq 100", element, {displayMode:false,throwOnError:false});$ , where $var element = document.getElementById("moose-equation-6c9f43c2-3eaf-49e8-9760-fc89c14fdc54");katex.render("T^\\dagger", element, {displayMode:false,throwOnError:false});$ is the non-dimensional temperature. This is useful to limit extreme temperatures in under-resolved regions of the mesh. We define this operation in a kernel, which we name clipTemperature.
Increase the viscosity and conductivity at the domain outlet (where the mesh is underresolved) in order to maintain a stable solution. The properties are modified to ramp the viscosity and conductivity between heights of $var element = document.getElementById("moose-equation-59b09765-27fc-4162-b1d9-e0c5c0f3073e");katex.render("4.6d_p", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-fb6cb45b-3d94-4b3b-bad6-4e87d1de2697");katex.render("5d_p", element, {displayMode:false,throwOnError:false});$ in a kernel which we name manipulateOutlet.

Next, the .udf file is used to setup initial conditions and conduct other initialization aspects in order to JIT-compile our kernels.

#include <math.h>
#include "udf.hpp"

static occa::kernel cliptKernel;  // clipping
static occa::kernel manipulateOutletKernel; // variable conductivity at the outlet

void uservp(nrs_t *nrs, double time, occa::memory o_U, occa::memory o_S,
            occa::memory o_UProp, occa::memory o_SProp)
{
  // pass the needed info into the outlet kernel
  mesh_t *mesh = nrs->meshV;
  manipulateOutletKernel(mesh->Nelements, nrs->fieldOffset, nrs->cds->fieldOffset[0],
               o_S, o_UProp, o_SProp, mesh->o_z);
}

void UDF_LoadKernels(occa::properties & kernelInfo)
{
  // tell NekRS to JIT compile our two kernels
  cliptKernel = oudfBuildKernel(kernelInfo, "clipTemperature");
  manipulateOutletKernel = oudfBuildKernel(kernelInfo, "manipulateOutlet");
}

void UDF_Setup(nrs_t *nrs)
{
  mesh_t * mesh = nrs->meshV;
  int n_gll_points = mesh->Np * mesh->Nelements;

  // apply initial conditions
  for (int n = 0; n < n_gll_points; ++n)
  {
    nrs->U[n + 0 * nrs->fieldOffset] = 0.0; // x-velocity
    nrs->U[n + 1 * nrs->fieldOffset] = 0.0; // y-velocity
    nrs->U[n + 2 * nrs->fieldOffset] = 1.0; // z-velocity
  }

  // set the udf.properties so that NekRS will modify the diffusive properties
  udf.properties = &uservp;
}

void UDF_ExecuteStep(nrs_t *nrs, double time, int tstep)
{
  // clip temperature on each time step
  mesh_t *mesh = nrs->cds->mesh[0];
  cds_t* cds = nrs->cds;
  cliptKernel(mesh->Nelements, cds->o_S);
}

Note that our two custom kernels are fundamentally different in character. The clipTemperature kernel is a postprocessing activity, so we explicitly call that kernel on each time step in the UDF_ExecuteStep function. Alternatively, the manipulateOutletKernel is changing the viscosity and conductivity near the outlet, which is modifying the actual governing equations themselves. NekRS contains a udf object which has multiple pointers to kernels which actually touch the governing equations. For our case, the udf.properties pointer is the interface for modifying the fluid properties, so we pass a function wrapping our kernel (uservp) to that variable so that NekRS can call the kernel at the appropriate location during execution. You can find the function signatures for the other interfaces in nekRS/src/udf/udf.hpp:


struct UDF {
  udfsetup0 setup0;
  udfsetup setup;
  udfloadKernels loadKernels;
  udfautoloadKernels autoloadKernels;
  udfautoloadPlugins autoloadPlugins;
  udfexecuteStep executeStep;
  udfuEqnSource uEqnSource;
  udfsEqnSource sEqnSource;
  udfproperties properties;
  udfdiv div;
  udfconv timeStepConverged;
  udfPreFluid preFluid;
  udfPostScalar postScalar;
};

You have already seen the udf.sEqnSource for applying a volumetric heat source in NekRS from MOOSE.

Finally, for this tutorial we are also using the legacy Fortran backend to modify some of our boundary condition sidesets (for demonstration's sake, the mesh may have been generated without sideset numbers, which NekRS needs). We do this manipulation in the pb67.usr file, in the usrdat2() subroutine.

c-----------------------------------------------------------------------
      subroutine useric(i,j,k,eg) ! set up initial conditions
      include 'SIZE'
      include 'TOTAL'
      include 'NEKUSE'
      integer i,j,k,e,eg

      return
      end
c-----------------------------------------------------------------------
      subroutine userchk
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat   ! This routine to modify element vertices
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat2()  ! This routine to modify mesh coordinates
      include 'SIZE'
      include 'TOTAL'

      integer e,f

      do iel=1,nelt
      do ifc=1,2*ndim
      if (cbc(ifc,iel,1).eq.'TOP') then  ! top surface
          cbc(ifc,iel,1) = 'O  '
          cbc(ifc,iel,2) = 'I  '
          bc(5,ifc,iel,1) = 1
       else if  (cbc(ifc,iel,1).eq.'BOT') then  ! bot surface
          cbc(ifc,iel,1) = 'v  '
          cbc(ifc,iel,2) = 't  '
          bc(5,ifc,iel,1) = 2
       else if  (cbc(ifc,iel,1).eq.'SW ') then    ! side wall of cylinder
          cbc(ifc,iel,1) = 'W  '
          cbc(ifc,iel,2) = 'I  '
          bc(5,ifc,iel,1) = 3
       else if  (cbc(ifc,iel,1).eq.'PW ') then  ! pebble surface
          cbc(ifc,iel,1) = 'WH  '
          cbc(ifc,iel,2) = 'fH  '
          bc(5,ifc,iel,1) = 4
       else if  (cbc(ifc,iel,1).eq.'C  ') then  ! chamfer surface
          cbc(ifc,iel,1) = 'W  '
          cbc(ifc,iel,2) = 'E  '
          bc(5,ifc,iel,1) = 5
       else
          cbc(ifc,iel,1) = 'E  '
          bc(5,ifc,iel,1) = 0
      endif
      enddo
      enddo

      do iel=1,nelt
      do ifc=1,2*ndim
        boundaryID(ifc,iel)=0
        if(cbc(ifc,iel,1) .eq. 'v ') boundaryID(ifc,iel)=1
        if(cbc(ifc,iel,1) .eq. 'O ') boundaryID(ifc,iel)=2
        if(cbc(ifc,iel,1) .eq. 'W ') boundaryID(ifc,iel)=3
        if(cbc(ifc,iel,1) .eq. 'WH ') boundaryID(ifc,iel)=4
      enddo
      enddo

      do iel=1,nelt
      do ifc=1,2*ndim
         boundaryIDt(ifc,iel) = 0
         if (cbc(ifc,iel,2) .eq. 't  ') boundaryIDt(ifc,iel) = 1
         if (cbc(ifc,iel,2) .eq. 'I  ') boundaryIDt(ifc,iel) = 2
         if (cbc(ifc,iel,2) .eq. 'I  ') boundaryIDt(ifc,iel) = 3
         if (cbc(ifc,iel,2) .eq. 'fH  ') boundaryIDt(ifc,iel) = 4
      enddo
      enddo

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat3
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------

The following lists how to interpret these various Fortran entities:

iel is a loop variable name used to indicate a loop over elements
ifc is a loop variable name used to indicate a loop over the faces on an element
cbc(ifc, iel, 1): sideset name for velocity
cbc(ifc, iel, 2): sideset name for temperature
bc(5, ifc, iel, 1): sideset ID for velocity
boundaryID(ifc, iel): sideset ID for velocity
boundaryIDt(ifc, iel): sideset ID for temperature

In other words, this function is essentially (i) changing the names associated with sidesets and then (ii) using those new names to define IDs for the sidesets.

CHT Coupling

In this section, MOOSE and NekRS are coupled for CHT.

Solid Input Files

The solid phase is solved with the MOOSE heat transfer module, and is described in the moose.i input. First we set up the mesh using a SphereMeshGenerator for each pebble and then repeating it 67 times at each pebble location.

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]
  [sphere]
    type = SphereMeshGenerator<<<{"description": "Generate a 3-D sphere mesh centered on the origin", "href": "../source/meshgenerators/SphereMeshGenerator.html"}>>>
    radius<<<{"description": "Sphere radius"}>>> = 0.03
    nr<<<{"description": "Number of radial elements"}>>> = 2
  []
  [cmbn]
    type = CombinerGenerator<<<{"description": "Combine multiple meshes (or copies of one mesh) together into one (disjoint) mesh.  Can optionally translate those meshes before combining them.", "href": "../source/meshgenerators/CombinerGenerator.html"}>>>
    inputs<<<{"description": "The input MeshGenerators.  This can either be N generators or 1 generator.  If only 1 is given then 'positions' must also be given."}>>> = sphere
    positions_file<<<{"description": "Alternative way to provide the position of each given mesh."}>>> = 'pebble_positions.txt'
  []
[]

Next, we define a temperature variable temp, and specify the governing equations and boundary conditions we will apply.

[Variables<<<{"href": "../syntax/Variables/index.html"}>>>]
  [temp]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 523.0
  []
[]

[Kernels<<<{"href": "../syntax/Kernels/index.html"}>>>]
  [hc]
    type = HeatConduction<<<{"description": "Diffusive heat conduction term $-\\nabla\\cdot(k\\nabla T)$ of the thermal energy conservation equation", "href": "../source/kernels/HeatConduction.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce<<<{"description": "Demonstrates the multiple ways that scalar values can be introduced into kernels, e.g. (controllable) constants, functions, and postprocessors. Implements the weak form $(\\psi_i, -f)$.", "href": "../source/kernels/BodyForce.html"}>>>
    value<<<{"description": "Coefficient to multiply by the body force term"}>>> = 338714.0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
  []
[]

[BCs<<<{"href": "../syntax/BCs/index.html"}>>>]
  [match_nek]
    type = MatchedValueBC<<<{"description": "Implements a NodalBC which equates two different Variables' values on a specified boundary.", "href": "../source/bcs/MatchedValueBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '0'
    v<<<{"description": "The variable whose value we are to match."}>>> = nek_temp
  []
[]

[Materials<<<{"href": "../syntax/Materials/index.html"}>>>]
  [hc]
    type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_values<<<{"description": "The values associated with the named properties"}>>> = '5.0'
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = 'thermal_conductivity'
  []
[]

[AuxVariables<<<{"href": "../syntax/AuxVariables/index.html"}>>>]
  [nek_temp]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 523.0
  []
  [flux]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
  []
[]

[AuxKernels<<<{"href": "../syntax/AuxKernels/index.html"}>>>]
  [flux]
    type = DiffusionFluxAux<<<{"description": "Compute components of flux vector for diffusion problems $(\\vec{J} = -D \\nabla C)$.", "href": "../source/auxkernels/DiffusionFluxAux.html"}>>>
    diffusion_variable<<<{"description": "The name of the variable"}>>> = temp
    component<<<{"description": "The desired component of flux."}>>> = normal
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation."}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = flux
    boundary<<<{"description": "The list of boundaries (ids or names) from the mesh where this object applies"}>>> = '0'
  []
[]

[MultiApps<<<{"href": "../syntax/MultiApps/index.html"}>>>]
  [nek]
    type = TransientMultiApp<<<{"description": "MultiApp for performing coupled simulations with the parent and sub-application both progressing in time.", "href": "../source/multiapps/TransientMultiApp.html"}>>>
    input_files<<<{"description": "The input file for each App.  If this parameter only contains one input file it will be used for all of the Apps.  When using 'positions_from_file' it is also admissable to provide one input_file per file."}>>> = 'nek.i'
    sub_cycling<<<{"description": "Set to true to allow this MultiApp to take smaller timesteps than the rest of the simulation.  More than one timestep will be performed for each parent application timestep"}>>> = true
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
  []
[]

[Transfers<<<{"href": "../syntax/Transfers/index.html"}>>>]
  [nek_temp]
    type = MultiAppNearestNodeTransfer<<<{"description": "Transfer the value to the target domain from the nearest node in the source domain.", "href": "../source/transfers/MultiAppNearestNodeTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = temperature
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_temp
    fixed_meshes<<<{"description": "Set to true when the meshes are not changing (ie, no movement or adaptivity).  This will cache nearest node neighbors to greatly speed up the transfer."}>>> = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer<<<{"description": "Transfer the value to the target domain from the nearest node in the source domain.", "href": "../source/transfers/MultiAppNearestNodeTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = flux
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = flux
    fixed_meshes<<<{"description": "Set to true when the meshes are not changing (ie, no movement or adaptivity).  This will cache nearest node neighbors to greatly speed up the transfer."}>>> = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = flux_integral
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = flux_integral
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = transfer_in
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = synchronize
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
  hide<<<{"description": "A list of the variables and postprocessors that should NOT be output to the Exodus file (may include Variables, ScalarVariables, and Postprocessor names)."}>>> = 'synchronize'
  interval = ${M}
[]

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [flux_integral]
    type = SideDiffusiveFluxIntegral<<<{"description": "Computes the integral of the diffusive flux over the specified boundary", "href": "../source/postprocessors/SideDiffusiveFluxIntegral.html"}>>>
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation. This must be provided if the variable is of finite element type"}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable which this postprocessor integrates"}>>> = 'temp'
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = temp
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
  []
  [min_pebble_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = temp
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = min
  []
  [volume]
    type = VolumePostprocessor<<<{"description": "Computes the volume of a specified block", "href": "../source/postprocessors/VolumePostprocessor.html"}>>>
  []
  [synchronize]
    type = Receiver<<<{"description": "Reports the value stored in this processor, which is usually filled in by another object. The Receiver does not compute its own value.", "href": "../source/postprocessors/Receiver.html"}>>>
    default<<<{"description": "The default value"}>>> = 1.0
  []
[]

The MOOSE heat transfer module will receive a wall temperature from NekRS in the form of an AuxVariable, so we define a receiver variable for the temperature, as nek_temp. The MOOSE heat transfer module will also send heat flux to NekRS, which we compute as another AuxVariable named flux, which we compute with a DiffusionFluxAux auxiliary kernel.

[AuxVariables<<<{"href": "../syntax/AuxVariables/index.html"}>>>]
  [nek_temp]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 523.0
  []
  [flux]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
  []
[]

[AuxKernels<<<{"href": "../syntax/AuxKernels/index.html"}>>>]
  [flux]
    type = DiffusionFluxAux<<<{"description": "Compute components of flux vector for diffusion problems $(\\vec{J} = -D \\nabla C)$.", "href": "../source/auxkernels/DiffusionFluxAux.html"}>>>
    diffusion_variable<<<{"description": "The name of the variable"}>>> = temp
    component<<<{"description": "The desired component of flux."}>>> = normal
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation."}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = flux
    boundary<<<{"description": "The list of boundaries (ids or names) from the mesh where this object applies"}>>> = '0'
  []
[]

We define a number of postprocessors for querying the solution as well as for normalizing the heat flux.

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [flux_integral]
    type = SideDiffusiveFluxIntegral<<<{"description": "Computes the integral of the diffusive flux over the specified boundary", "href": "../source/postprocessors/SideDiffusiveFluxIntegral.html"}>>>
    diffusivity<<<{"description": "The name of the diffusivity material property that will be used in the flux computation. This must be provided if the variable is of finite element type"}>>> = thermal_conductivity
    variable<<<{"description": "The name of the variable which this postprocessor integrates"}>>> = 'temp'
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = temp
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = max
  []
  [min_pebble_T]
    type = NodalExtremeValue<<<{"description": "Finds either the min or max elemental value of a variable over the domain.", "href": "../source/postprocessors/NodalExtremeValue.html"}>>>
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = temp
    value_type<<<{"description": "Type of extreme value to return. 'max' returns the maximum value. 'min' returns the minimum value. 'max_abs' returns the maximum of the absolute value."}>>> = min
  []
  [volume]
    type = VolumePostprocessor<<<{"description": "Computes the volume of a specified block", "href": "../source/postprocessors/VolumePostprocessor.html"}>>>
  []
  [synchronize]
    type = Receiver<<<{"description": "Reports the value stored in this processor, which is usually filled in by another object. The Receiver does not compute its own value.", "href": "../source/postprocessors/Receiver.html"}>>>
    default<<<{"description": "The default value"}>>> = 1.0
  []
[]

Finally, we add a TransientMultiApp that will run a MOOSE-wrapped NekRS simulation. Then, we add three different transfers to/from NekRS:

MultiAppNearestNodeTransfer to send the heat flux from MOOSE to NekRS
MultiAppNearestNodeTransfer to send temperature from NekRS to MOOSE
MultiAppPostprocessorTransfer to normalize the heat flux sent to NekRS

[MultiApps<<<{"href": "../syntax/MultiApps/index.html"}>>>]
  [nek]
    type = TransientMultiApp<<<{"description": "MultiApp for performing coupled simulations with the parent and sub-application both progressing in time.", "href": "../source/multiapps/TransientMultiApp.html"}>>>
    input_files<<<{"description": "The input file for each App.  If this parameter only contains one input file it will be used for all of the Apps.  When using 'positions_from_file' it is also admissable to provide one input_file per file."}>>> = 'nek.i'
    sub_cycling<<<{"description": "Set to true to allow this MultiApp to take smaller timesteps than the rest of the simulation.  More than one timestep will be performed for each parent application timestep"}>>> = true
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
  []
[]

[Transfers<<<{"href": "../syntax/Transfers/index.html"}>>>]
  [nek_temp]
    type = MultiAppNearestNodeTransfer<<<{"description": "Transfer the value to the target domain from the nearest node in the source domain.", "href": "../source/transfers/MultiAppNearestNodeTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = temperature
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = nek_temp
    fixed_meshes<<<{"description": "Set to true when the meshes are not changing (ie, no movement or adaptivity).  This will cache nearest node neighbors to greatly speed up the transfer."}>>> = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer<<<{"description": "Transfer the value to the target domain from the nearest node in the source domain.", "href": "../source/transfers/MultiAppNearestNodeTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = flux
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = flux
    fixed_meshes<<<{"description": "Set to true when the meshes are not changing (ie, no movement or adaptivity).  This will cache nearest node neighbors to greatly speed up the transfer."}>>> = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = flux_integral
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = flux_integral
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer<<<{"description": "Transfers postprocessor data between the master application and sub-application(s).", "href": "../source/transfers/MultiAppPostprocessorTransfer.html"}>>>
    to_postprocessor<<<{"description": "The name of the Postprocessor in the MultiApp to transfer the value to.  This should most likely be a Reporter Postprocessor."}>>> = transfer_in
    from_postprocessor<<<{"description": "The name of the Postprocessor in the Master to transfer the value from."}>>> = synchronize
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
  hide<<<{"description": "A list of the variables and postprocessors that should NOT be output to the Exodus file (may include Variables, ScalarVariables, and Postprocessor names)."}>>> = 'synchronize'
  interval = ${M}
[]

Fluid Input Files

The Nek wrapping is described in the nek.i input file. We first define a few file-local variables, and then build a mesh mirror with a NekRSMesh. By setting boundary = '4', we indicate that boundary 4 will be coupled via CHT.

Re = 1460.0
dp = 0.06
cylinder_diameter = ${fparse 4.4 * dp}
density = 3.645
C = 3121.0
mu = 2.93e-5
power = 2400.0
inlet_area = ${fparse pi * cylinder_diameter^2 / 4.0}

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]
  type = NekRSMesh
  boundary = 4
  scaling = ${dp}
[]

Next, we define additional parameters to describe how NekRS interacts with MOOSE with the NekRSProblem. The NekRS input files are in nondimensional form, so we must indicate all the characteristic scales so that data transfers with a dimensional MOOSE application are performed correctly. Then, we add the necessary FieldTransfers to write heat flux into NekRS and to read out the temperature and components of velocity.

[Problem<<<{"href": "../syntax/Problem/index.html"}>>>]
  type = NekRSProblem
  casename<<<{"description": "Case name for the NekRS input files; this is <case> in <case>.par, <case>.udf, <case>.oudf, and <case>.re2."}>>> = 'pb67'
  n_usrwrk_slots<<<{"description": "Number of slots to allocate in nrs->usrwrk to hold fields either related to coupling (which will be populated by Cardinal), or other custom usages, such as a distance-to-wall calculation"}>>> = 2

  [Dimensionalize<<<{"href": "../syntax/Problem/Dimensionalize/index.html"}>>>]
    L<<<{"description": "Reference length"}>>> = ${dp}
    U<<<{"description": "Reference velocity"}>>> = '${fparse Re * mu / density / dp}'
    T<<<{"description": "Reference temperature"}>>> = 523.0
    dT<<<{"description": "Reference temperature difference"}>>> = '${fparse power * dp / Re / inlet_area / mu / C}'
    rho<<<{"description": "Reference density"}>>> = ${density}
    Cp<<<{"description": "Reference isobaric specific heat"}>>> = ${C}
  []

  [FieldTransfers<<<{"href": "../syntax/Problem/FieldTransfers/index.html"}>>>]
    [flux]
      type = NekBoundaryFlux<<<{"description": "Reads/writes boundary flux data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = to_nek
      usrwrk_slot<<<{"description": "When 'direction = to_nek', the slot(s) in the usrwrk array to write the incoming data; provide one entry for each quantity being passed"}>>> = 0
    []
    [temperature]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
    [velocity_x]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
    [velocity_y]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
    [velocity_z]
      type = NekFieldVariable<<<{"description": "Reads/writes volumetric field data between NekRS and MOOSE."}>>>
      direction<<<{"description": "Direction in which to send data"}>>> = from_nek
    []
  []

  synchronization_interval = parent_app
[]

For time stepping, we will allow NekRS to control its own time stepping by using the NekTimeStepper.

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Transient

  [TimeStepper<<<{"href": "../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = NekTimeStepper
  []
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
  interval = 100
[]

Then, we define a few postprocessors to use for querying the solution.

[Postprocessors<<<{"href": "../syntax/Postprocessors/index.html"}>>>]
  [max_nek_T]
    type = NekVolumeExtremeValue<<<{"description": "Extreme value (max/min) of a field over the NekRS mesh", "href": "../source/postprocessors/NekVolumeExtremeValue.html"}>>>
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    value_type<<<{"description": "Whether to give the maximum or minimum extreme value"}>>> = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue<<<{"description": "Extreme value (max/min) of a field over the NekRS mesh", "href": "../source/postprocessors/NekVolumeExtremeValue.html"}>>>
    field<<<{"description": "Field to apply this object to"}>>> = temperature
    value_type<<<{"description": "Whether to give the maximum or minimum extreme value"}>>> = min
  []
  [average_nek_pebble_T]
    type = NekSideAverage<<<{"description": "Average of a field over a boundary of the NekRS mesh", "href": "../source/postprocessors/NekSideAverage.html"}>>>
    boundary<<<{"description": "Boundary ID(s) for which to compute the postprocessor"}>>> = '4'
    field<<<{"description": "Field to apply this object to"}>>> = temperature
  []
[]

Execution and Postprocessing

To run the coupled NekRS-MOOSE calculation,


mpiexec -np 500 cardinal-opt -i moose.i

This will run with 500 MPI processes. When the simulation has finished, you will have created a number of different output files:

moose_out.e, an Exodus file with the MOOSE solution for the NekRS-MOOSE calculation
moose_out_nek0.e, an Exodus file with the NekRS solution that was ultimately transferred in/out of MOOSE
pb670.f<n>, a (custom format) NekRS output file with the NekRS solution; to convert to a format viewable in Paraview, consult the NekRS documentation

Figure 4 shows the instantaneous velocity (left) and temperature (right) predicted by NekRS, in non-dimensional form. This solution is visualized from the NekRS native output files.

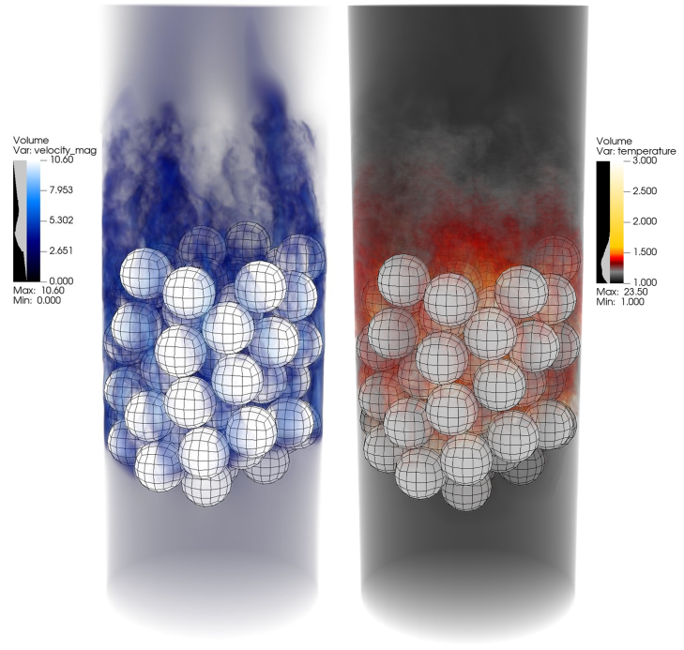
Figure 4: Instantaneous velocity (left) and temperature (right) predicted by NekRS, in non-dimensional form.

References

Y. Lan, P. Fischer, E. Merzari, and M. Min. All-hex meshing strategies for densely packed spheres. arXiv, 2021. URL: https://arxiv.org/abs/2106.00196.

@article{lan,
    author = "Lan, Y. and Fischer, P. and Merzari, E. and Min, M.",
    title = "All-Hex Meshing Strategies for Densely Packed Spheres",
    year = "2021",
    journal = "arXiv",
    url = "https://arxiv.org/abs/2106.00196"
}

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/pb67.par)

[GENERAL]
  polynomialOrder = 7
  stopAt = endTime
  endTime = 500

  dt = 2.0e-05
  timeStepper = tombo2
  subCyclingSteps = 2

  writeControl = steps
  writeInterval = 2000

  filtering = hpfrt
  filterWeight = 0.2/${dt}
  filterModes = 2

[PRESSURE]
  residualTol = 1e-04
  preconditioner = multigrid
  smootherType = chebyshev+jac
  initialGuess = projectionAconj + nVector = 30

[VELOCITY]
  boundaryTypeMap = inlet, outlet, wall, wall
  density = 1.0
  viscosity = -1460.0
  residualTol = 1e-06

[TEMPERATURE]
  boundaryTypeMap = t, I, I, f
  residualTol = 1e-06
  rhoCp = 1.0
  conductivity = -1036.0

(tutorials/pebble_67/pb67.oudf)

void velocityDirichletConditions(bcData *bc)
{
  bc->u = 0.0;
  bc->v = 0.0;
  bc->w = 1.0;
}

// Stabilized outflow (Dong et al)
void pressureDirichletConditions(bcData *bc)
{
  const dfloat iU0delta = 20.0;
  const dfloat un = bc->u*bc->nx + bc->v*bc->ny + bc->w*bc->nz;
  const dfloat s0 = 0.5 * (1.0 - tanh(un*iU0delta));
  bc->p = -0.5 * (bc->u*bc->u + bc->v*bc->v + bc->w*bc->w) * s0;
}

void scalarDirichletConditions(bcData *bc)
{
  bc->s = 0.0;
}

void scalarNeumannConditions(bcData *bc)
{
  // note: when running with Cardinal, Cardinal will allocate the usrwrk
  // array. If running with NekRS standalone (e.g. nrsmpi), you need to
  // replace the usrwrk with some other value or allocate it youself from
  // the udf and populate it with values.
  bc->flux = bc->usrwrk[bc->idM];
}

@kernel void clipTemperature(const dlong Nelements,
                 @restrict dfloat * TEMP)
{

  for (dlong e=0;e<Nelements;++e;@outer(0))
  {
    for (int n=0;n<p_Np;++n;@inner(0))
    {
      const int id = e * p_Np + n;
      const dfloat clip_temperature_max = 100.0;
      const dfloat clip_temperature_min = 0.0;

      if (TEMP[id] > clip_temperature_max)
        TEMP[id] = clip_temperature_max;
      if (TEMP[id] < clip_temperature_min)
        TEMP[id] = clip_temperature_min;
    }
  }
}

@kernel void manipulateOutlet(const dlong Nelements,
                    const dlong uOffset,
                    const dlong sOffset,
                    @restrict const dfloat * TEMP,
                    @restrict dfloat * UPROP,
                    @restrict dfloat * SPROP,
                    @restrict const dfloat * Z)
{
  for (dlong e=0;e<Nelements;++e;@outer(0))
  {
    for (int n=0;n<p_Np;++n;@inner(0))
    {
      const int id = e*p_Np + n;

       // change outlet viscosity/conductivity

      // my current z position
      dfloat local_z = Z[id];

      // height above which I want to manipulate viscosity and conductivity;
      // I will apply a ramping of viscosity between z1 and z2, and set a very
      // high value above z2
      dfloat z1 = 4.6;
      dfloat z2 = 5.0;

      dfloat rho = 1.0;
      dfloat visc = 1.0 / 10000.0;
      dfloat cond = 1.0 / 7100.0;
      dfloat Cp = 1.0;

      // increase viscosity and conductivity near outlet
      dfloat factor = 1.0;
      if (local_z >= z2)
        factor = 101.0;
      else if (local_z > z1 && local_z < z2)
        factor = 1.0 + 100.0 * (local_z - z1) / (z2 - z1);

      visc = factor * visc;
      cond = factor * cond;

      UPROP[id + 0*uOffset] = visc;
      SPROP[id + 0*sOffset] = cond;
      UPROP[id + 1*uOffset] = rho;
      SPROP[id + 1*sOffset] = rho*Cp;
    }
  }
}

(tutorials/pebble_67/pb67.udf)

#include <math.h>
#include "udf.hpp"

static occa::kernel cliptKernel;  // clipping
static occa::kernel manipulateOutletKernel; // variable conductivity at the outlet

void uservp(nrs_t *nrs, double time, occa::memory o_U, occa::memory o_S,
            occa::memory o_UProp, occa::memory o_SProp)
{
  // pass the needed info into the outlet kernel
  mesh_t *mesh = nrs->meshV;
  manipulateOutletKernel(mesh->Nelements, nrs->fieldOffset, nrs->cds->fieldOffset[0],
               o_S, o_UProp, o_SProp, mesh->o_z);
}

void UDF_LoadKernels(occa::properties & kernelInfo)
{
  // tell NekRS to JIT compile our two kernels
  cliptKernel = oudfBuildKernel(kernelInfo, "clipTemperature");
  manipulateOutletKernel = oudfBuildKernel(kernelInfo, "manipulateOutlet");
}

void UDF_Setup(nrs_t *nrs)
{
  mesh_t * mesh = nrs->meshV;
  int n_gll_points = mesh->Np * mesh->Nelements;

  // apply initial conditions
  for (int n = 0; n < n_gll_points; ++n)
  {
    nrs->U[n + 0 * nrs->fieldOffset] = 0.0; // x-velocity
    nrs->U[n + 1 * nrs->fieldOffset] = 0.0; // y-velocity
    nrs->U[n + 2 * nrs->fieldOffset] = 1.0; // z-velocity
  }

  // set the udf.properties so that NekRS will modify the diffusive properties
  udf.properties = &uservp;
}

void UDF_ExecuteStep(nrs_t *nrs, double time, int tstep)
{
  // clip temperature on each time step
  mesh_t *mesh = nrs->cds->mesh[0];
  cds_t* cds = nrs->cds;
  cliptKernel(mesh->Nelements, cds->o_S);
}

(tutorials/pebble_67/pb67.usr)

c-----------------------------------------------------------------------
      subroutine useric(i,j,k,eg) ! set up initial conditions
      include 'SIZE'
      include 'TOTAL'
      include 'NEKUSE'
      integer i,j,k,e,eg

      return
      end
c-----------------------------------------------------------------------
      subroutine userchk
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat   ! This routine to modify element vertices
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat2()  ! This routine to modify mesh coordinates
      include 'SIZE'
      include 'TOTAL'

      integer e,f

      do iel=1,nelt
      do ifc=1,2*ndim
      if (cbc(ifc,iel,1).eq.'TOP') then  ! top surface
          cbc(ifc,iel,1) = 'O  '
          cbc(ifc,iel,2) = 'I  '
          bc(5,ifc,iel,1) = 1
       else if  (cbc(ifc,iel,1).eq.'BOT') then  ! bot surface
          cbc(ifc,iel,1) = 'v  '
          cbc(ifc,iel,2) = 't  '
          bc(5,ifc,iel,1) = 2
       else if  (cbc(ifc,iel,1).eq.'SW ') then    ! side wall of cylinder
          cbc(ifc,iel,1) = 'W  '
          cbc(ifc,iel,2) = 'I  '
          bc(5,ifc,iel,1) = 3
       else if  (cbc(ifc,iel,1).eq.'PW ') then  ! pebble surface
          cbc(ifc,iel,1) = 'WH  '
          cbc(ifc,iel,2) = 'fH  '
          bc(5,ifc,iel,1) = 4
       else if  (cbc(ifc,iel,1).eq.'C  ') then  ! chamfer surface
          cbc(ifc,iel,1) = 'W  '
          cbc(ifc,iel,2) = 'E  '
          bc(5,ifc,iel,1) = 5
       else
          cbc(ifc,iel,1) = 'E  '
          bc(5,ifc,iel,1) = 0
      endif
      enddo
      enddo

      do iel=1,nelt
      do ifc=1,2*ndim
        boundaryID(ifc,iel)=0
        if(cbc(ifc,iel,1) .eq. 'v ') boundaryID(ifc,iel)=1
        if(cbc(ifc,iel,1) .eq. 'O ') boundaryID(ifc,iel)=2
        if(cbc(ifc,iel,1) .eq. 'W ') boundaryID(ifc,iel)=3
        if(cbc(ifc,iel,1) .eq. 'WH ') boundaryID(ifc,iel)=4
      enddo
      enddo

      do iel=1,nelt
      do ifc=1,2*ndim
         boundaryIDt(ifc,iel) = 0
         if (cbc(ifc,iel,2) .eq. 't  ') boundaryIDt(ifc,iel) = 1
         if (cbc(ifc,iel,2) .eq. 'I  ') boundaryIDt(ifc,iel) = 2
         if (cbc(ifc,iel,2) .eq. 'I  ') boundaryIDt(ifc,iel) = 3
         if (cbc(ifc,iel,2) .eq. 'fH  ') boundaryIDt(ifc,iel) = 4
      enddo
      enddo

      return
      end
c-----------------------------------------------------------------------
      subroutine usrdat3
      include 'SIZE'
      include 'TOTAL'

      return
      end
c-----------------------------------------------------------------------

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/moose.i)

[Mesh]
  [sphere]
    type = SphereMeshGenerator
    radius = 0.03
    nr = 2
  []
  [cmbn]
    type = CombinerGenerator
    inputs = sphere
    positions_file = 'pebble_positions.txt'
  []
[]

[Variables]
  [temp]
    initial_condition = 523.0
  []
[]

[Kernels]
  [hc]
    type = HeatConduction
    variable = temp
  []
  [heat] # approximate value to get desired power
    type = BodyForce
    value = 338714.0
    variable = temp
  []
[]

[BCs]
  [match_nek]
    type = MatchedValueBC
    variable = temp
    boundary = '0'
    v = nek_temp
  []
[]

[Materials]
  [hc]
    type = GenericConstantMaterial
    prop_values = '5.0'
    prop_names = 'thermal_conductivity'
  []
[]

[AuxVariables]
  [nek_temp]
    initial_condition = 523.0
  []
  [flux]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [flux]
    type = DiffusionFluxAux
    diffusion_variable = temp
    component = normal
    diffusivity = thermal_conductivity
    variable = flux
    boundary = '0'
  []
[]

[MultiApps]
  [nek]
    type = TransientMultiApp
    input_files = 'nek.i'
    sub_cycling = true
    execute_on = timestep_end
  []
[]

[Transfers]
  [nek_temp]
    type = MultiAppNearestNodeTransfer
    source_variable = temperature
    from_multi_app = nek
    variable = nek_temp
    fixed_meshes = true
  []
  [flux]
    type = MultiAppNearestNodeTransfer
    source_variable = flux
    to_multi_app = nek
    variable = flux
    fixed_meshes = true
  []
  [flux_integral_to_nek]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = flux_integral
    from_postprocessor = flux_integral
    to_multi_app = nek
  []
  [synchronize_in]
    type = MultiAppPostprocessorTransfer
    to_postprocessor = transfer_in
    from_postprocessor = synchronize
    to_multi_app = nek
  []
[]

t_nek = ${fparse 3.067e-01 * 2.0e-5}
M = 100.0

[Executioner]
  type = Transient
  num_steps = 10000
  dt = ${fparse M * t_nek}
  nl_rel_tol = 1e-6
  nl_abs_tol = 1e-10
[]

[Outputs]
  exodus = true
  hide = 'synchronize'
  interval = ${M}
[]

[Postprocessors]
  [flux_integral]
    type = SideDiffusiveFluxIntegral
    diffusivity = thermal_conductivity
    variable = 'temp'
    boundary = '0'
  []
  [max_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = max
  []
  [min_pebble_T]
    type = NodalExtremeValue
    variable = temp
    value_type = min
  []
  [volume]
    type = VolumePostprocessor
  []
  [synchronize]
    type = Receiver
    default = 1.0
  []
[]

(tutorials/pebble_67/nek.i)

Re = 1460.0
dp = 0.06
cylinder_diameter = ${fparse 4.4 * dp}
density = 3.645
C = 3121.0
mu = 2.93e-5
power = 2400.0
inlet_area = ${fparse pi * cylinder_diameter^2 / 4.0}

[Mesh]
  type = NekRSMesh
  boundary = 4
  scaling = ${dp}
[]

[Problem]
  type = NekRSProblem
  casename = 'pb67'
  n_usrwrk_slots = 2

  [Dimensionalize]
    L = ${dp}
    U = ${fparse Re * mu / density / dp}
    T = 523.0
    dT = ${fparse power * dp / Re / inlet_area / mu / C}
    rho = ${density}
    Cp = ${C}
  []

  [FieldTransfers]
    [flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_x]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_y]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_z]
      type = NekFieldVariable
      direction = from_nek
    []
  []

  synchronization_interval = parent_app
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  interval = 100
[]

[Postprocessors]
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
  [average_nek_pebble_T]
    type = NekSideAverage
    boundary = '4'
    field = temperature
  []
[]

(tutorials/pebble_67/nek.i)

Re = 1460.0
dp = 0.06
cylinder_diameter = ${fparse 4.4 * dp}
density = 3.645
C = 3121.0
mu = 2.93e-5
power = 2400.0
inlet_area = ${fparse pi * cylinder_diameter^2 / 4.0}

[Mesh]
  type = NekRSMesh
  boundary = 4
  scaling = ${dp}
[]

[Problem]
  type = NekRSProblem
  casename = 'pb67'
  n_usrwrk_slots = 2

  [Dimensionalize]
    L = ${dp}
    U = ${fparse Re * mu / density / dp}
    T = 523.0
    dT = ${fparse power * dp / Re / inlet_area / mu / C}
    rho = ${density}
    Cp = ${C}
  []

  [FieldTransfers]
    [flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_x]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_y]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_z]
      type = NekFieldVariable
      direction = from_nek
    []
  []

  synchronization_interval = parent_app
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  interval = 100
[]

[Postprocessors]
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
  [average_nek_pebble_T]
    type = NekSideAverage
    boundary = '4'
    field = temperature
  []
[]

(tutorials/pebble_67/nek.i)

Re = 1460.0
dp = 0.06
cylinder_diameter = ${fparse 4.4 * dp}
density = 3.645
C = 3121.0
mu = 2.93e-5
power = 2400.0
inlet_area = ${fparse pi * cylinder_diameter^2 / 4.0}

[Mesh]
  type = NekRSMesh
  boundary = 4
  scaling = ${dp}
[]

[Problem]
  type = NekRSProblem
  casename = 'pb67'
  n_usrwrk_slots = 2

  [Dimensionalize]
    L = ${dp}
    U = ${fparse Re * mu / density / dp}
    T = 523.0
    dT = ${fparse power * dp / Re / inlet_area / mu / C}
    rho = ${density}
    Cp = ${C}
  []

  [FieldTransfers]
    [flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_x]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_y]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_z]
      type = NekFieldVariable
      direction = from_nek
    []
  []

  synchronization_interval = parent_app
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  interval = 100
[]

[Postprocessors]
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
  [average_nek_pebble_T]
    type = NekSideAverage
    boundary = '4'
    field = temperature
  []
[]

(tutorials/pebble_67/nek.i)

Re = 1460.0
dp = 0.06
cylinder_diameter = ${fparse 4.4 * dp}
density = 3.645
C = 3121.0
mu = 2.93e-5
power = 2400.0
inlet_area = ${fparse pi * cylinder_diameter^2 / 4.0}

[Mesh]
  type = NekRSMesh
  boundary = 4
  scaling = ${dp}
[]

[Problem]
  type = NekRSProblem
  casename = 'pb67'
  n_usrwrk_slots = 2

  [Dimensionalize]
    L = ${dp}
    U = ${fparse Re * mu / density / dp}
    T = 523.0
    dT = ${fparse power * dp / Re / inlet_area / mu / C}
    rho = ${density}
    Cp = ${C}
  []

  [FieldTransfers]
    [flux]
      type = NekBoundaryFlux
      direction = to_nek
      usrwrk_slot = 0
    []
    [temperature]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_x]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_y]
      type = NekFieldVariable
      direction = from_nek
    []
    [velocity_z]
      type = NekFieldVariable
      direction = from_nek
    []
  []

  synchronization_interval = parent_app
[]

[Executioner]
  type = Transient

  [TimeStepper]
    type = NekTimeStepper
  []
[]

[Outputs]
  exodus = true
  interval = 100
[]

[Postprocessors]
  [max_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = max
  []
  [min_nek_T]
    type = NekVolumeExtremeValue
    field = temperature
    value_type = min
  []
  [average_nek_pebble_T]
    type = NekSideAverage
    boundary = '4'
    field = temperature
  []
[]

Geometry and Computational Model
CHT Coupling
Execution and Postprocessing
References