Brayton Cycle

Introduction

The Brayton cycle is the ideal thermodynamic cycle for gas-turbine engines. Usually, it is used in an open system, where gas is drawn in from the environment and exhausted back into the environment. However, for some analyses, it is simpler to analyze the system as if it were a closed system that cycles the same working fluid in a closed loop, which can be done without significant loss of accuracy. Here we discuss how both open and closed cycles can be modeled.

In its simplest form, a Brayton cycle requires the following elements:

  • A heat source to add thermal energy to the working gas,

  • A heat sink to remove thermal energy from the working gas (in an open system, exhaust into the environment serves this function),

  • A compressor to compress the working gas, and

  • A turbine to expand the working gas.

Usually, the compressor and turbine are operated on the same shaft. In steady operation, the work the turbine provides to the shaft is partially consumed by the compressor when it applies work to the working fluid. The remainder can be used for the application's purposes, like electricity generation via a generator on the shaft. In practice, when starting up a Brayton engine, the turbine is not yet applying work to the shaft, and thus the compressor is not functioning either. Thus, a motor is used to drive the shaft until the cycle can sustain itself.

Example

Now an example will be given, first discussing the commonalities between the open and closed cycles and then describing the differences in the following sections.

The turbo-machinery setup for this example consists of a shaft, motor, compressor, turbine, and generator. The Shaft component connects them and specifies the initial shaft speed (here equal to zero since we are starting from rest):

[Components]
  [shaft]
    type = Shaft
    connected_components = 'motor compressor turbine generator'
    initial_speed = ${speed_initial}
  []
[]

As mentioned previously, when starting up, a motor is needed, so we use ShaftConnectedMotor:

[Components]
  [motor]
    type = ShaftConnectedMotor
    inertia = ${I_motor}
    torque = 0 # controlled
  []
[]

The torque parameter is set to an arbitrary value, since this parameter is controlled using the control logic system:

[ControlLogic]
  [motor_ctrl]
    type = TimeFunctionComponentControl
    component = motor
    parameter = torque
    function = motor_torque_fn
  []
[]

The function chosen here is a linear ramp up from zero and back down to zero,

τmotor(t)={τmotor,maxt1t0≤t≤t1τmotor,max−τmotor,maxt2−t1(t−t1)t1≤t≤t20t>t2\eqp\tau_\text{motor}(t) = \left\{\begin{array}{l l} \frac{\tau_\text{motor,max}}{t_1} t & 0 \leq t \leq t_1\\ \tau_\text{motor,max} - \frac{\tau_\text{motor,max}}{t_2 - t_1}(t - t_1) & t_1 \leq t \leq t_2\\ 0 & t > t_2\\ \end{array}\right. \eqp

This is accomplished with a PiecewiseLinear function:

[Functions]
  [motor_torque_fn]
    type = PiecewiseLinear
    x = '0 ${t1} ${t2}'
    y = '0 ${motor_torque_max} 0'
  []
[]

The compressor and turbine components are modeled using ShaftConnectedCompressor1Phase:

[Components]
  [compressor]
    type = ShaftConnectedCompressor1Phase
    position = '${x2} 0 0'
    inlet = 'pipe1:out'
    outlet = 'pipe2:in'
    A_ref = ${A_ref_comp}
    volume = ${V_comp}

    omega_rated = ${speed_rated}
    mdot_rated = ${rated_mfr}
    c0_rated = ${c0_rated_comp}
    rho0_rated = ${rho0_rated_comp}

    speeds = '0.5208 0.6250 0.7292 0.8333 0.9375'
    Rp_functions = 'rp_comp1 rp_comp2 rp_comp3 rp_comp4 rp_comp5'
    eff_functions = 'eff_comp1 eff_comp2 eff_comp3 eff_comp4 eff_comp5'

    min_pressure_ratio = 1.0

    speed_cr_I = 0
    inertia_const = ${I_comp}
    inertia_coeff = '${I_comp} 0 0 0'

    # assume no shaft friction
    speed_cr_fr = 0
    tau_fr_const = 0
    tau_fr_coeff = '0 0 0 0'

    use_scalar_variables = false
  []
[]
[Components]
  [turbine]
    type = ShaftConnectedCompressor1Phase
    position = '${x5} 0 0'
    inlet = 'pipe4:out'
    outlet = 'pipe5:in'
    A_ref = ${A_ref_turb}
    volume = ${V_turb}

    treat_as_turbine = true

    omega_rated = ${speed_rated}
    mdot_rated = ${rated_mfr}
    c0_rated = ${c0_rated_comp}
    rho0_rated = ${rho0_rated_comp}

    speeds = '0 0.5208 0.6250 0.7292 0.8333 0.9375'
    Rp_functions = 'rp_turb0 rp_turb1 rp_turb2 rp_turb3 rp_turb4 rp_turb5'
    eff_functions = 'eff_turb1 eff_turb1 eff_turb2 eff_turb3 eff_turb4 eff_turb5'

    min_pressure_ratio = 1.0

    speed_cr_I = 0
    inertia_const = ${I_turb}
    inertia_coeff = '${I_turb} 0 0 0'

    # assume no shaft friction
    speed_cr_fr = 0
    tau_fr_const = 0
    tau_fr_coeff = '0 0 0 0'

    use_scalar_variables = false
  []
[]

The pressure ratio curves are adapted from Guillen and Wendt (2020). In this reference, these curves are given as rp(m˙,ω)r_p(\dot{m}, \omega), rather than rp(ν,α)r_p(\nu, \alpha), so the curves were processed beforehand. As is often the case, there was data needed for these curves that was not available. For example,

ν≡(m˙ρ0, inc0, in)(m˙ρ0, inc0, in)rated\eqc\nu \equiv \frac{ (\frac{\dot{m}}{\rho_{\text{0, in}} c_{\text{0, in}}}) } { (\frac{\dot{m}}{\rho_{\text{0, in}} c_{\text{0, in}}})_{\text{rated}} } \eqc

but values for ρ0\rho_0 and c0c_0 are not known, only a rated mass flow rate m˙rated\dot{m}_\text{rated} was known, so ν\nu was approximated as

ν≈m˙m˙rated\eqc\nu \approx \frac{\dot{m}}{\dot{m}_\text{rated}} \eqc

which assumes ρ0, inc0, in≈(ρ0, inc0, in)rated\rho_{\text{0, in}} c_{\text{0, in}} \approx (\rho_{\text{0, in}} c_{\text{0, in}})_\text{rated}. Similarly,

α≈ωωrated\eqp\alpha \approx \frac{\omega}{\omega_\text{rated}} \eqp

The resulting curves are shown in Figure 1:

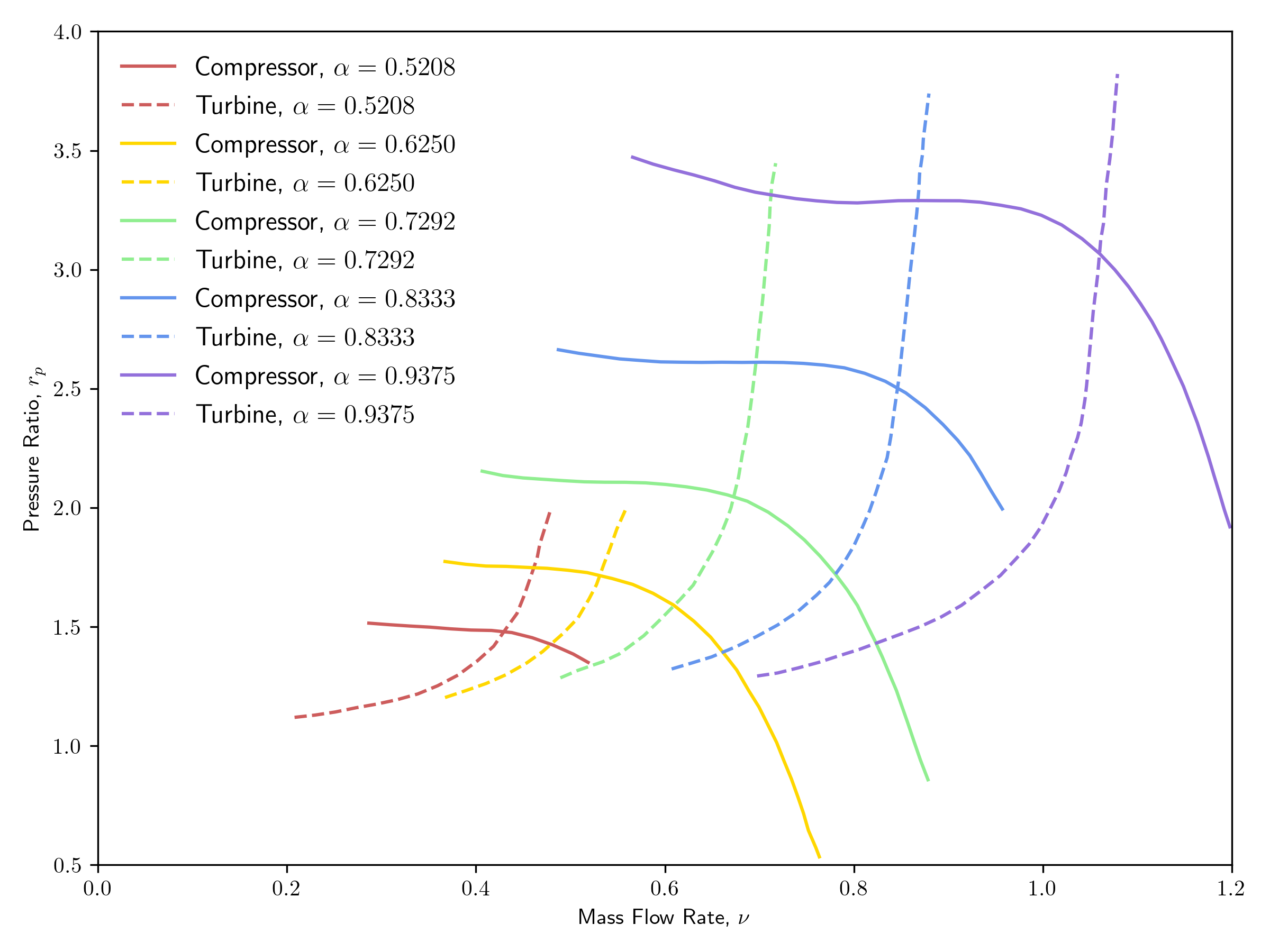
Figure 1: Pressure ratio curves for the compressor and turbine.

The efficiencies of both the compressor and turbine were set to constant values.

Finally, a generator is modeled using a ShaftConnectedMotor by using a negative torque of the form

τgen(ω)=−aω\eqc\tau_\text{gen}(\omega) = -a \omega \eqc

where aa is a positive value. This is accomplished as follows:

[Components]
  [generator]
    type = ShaftConnectedMotor
    inertia = ${I_generator}
    torque = generator_torque_fn
  []
[]

with the following function:

[Functions]
  [generator_torque_fn]
    type = ParsedFunction
    expression = 'slope * t'
    symbol_names = 'slope'
    symbol_values = '${generator_torque_per_shaft_speed}'
  []
[]

Closed Brayton Cycle

The model discussed in this section can be found in the following input file: closed_brayton_cycle.i.

In the closed cycle, a strong convection source term is applied to bring the working fluid back to near the ambient temperature:

[Components]
  [cooling]
    type = HeatTransferFromSpecifiedTemperature1Phase
    flow_channel = pipe6
    T_wall = ${T_cold}
    Hw = htc_wall_fn
  []
[]

Open Brayton Cycle

The model discussed in this section can be found in the following input file: open_brayton_cycle.i.

In the open cycle, instead of a heat sink, there is an inlet connected to the compressor inlet piping, and an outlet connected to the turbine outlet piping. For the inlet, the stagnation pressure and temperature (p0,T0)(p_0, T_0) formulation is appropriate, since the environment can be approximated to be at rest. The ambient pressure and temperature can then be used for p0p_0 and T0T_0, respectively:

[Components]
  [inlet]
    type = InletStagnationPressureTemperature1Phase
    input = 'pipe1:in'
    p0 = ${p_ambient}
    T0 = ${T_ambient}
  []
[]

There is a single outlet formulation, which specifies the ambient pressure:

[Components]
  [outlet]
    type = Outlet1Phase
    input = 'pipe5:out'
    p = ${p_ambient}
  []
[]

Results

Figure 2 and Figure 3 show the shaft speed transient for the open and closed cycles, respectively. The shaft speed profile indicates that the motor torque is fairly dominant in this example, as the profile appears to be an integral of the motor torque profile that was used; the motor torque was ramped up from zero to a max at t=t1t=t_1 and then back down to zero at t=t2t=t_2. The profile seen here may not necessarily be realistic, for several reasons, including the following:

  • Moments of inertia of the various shaft components were chosen arbitrarily,

  • The motor torque profile was chosen arbitrarily,

  • The generator torque relationship was chosen arbitrarily, and

  • Friction losses on the shaft were omitted.

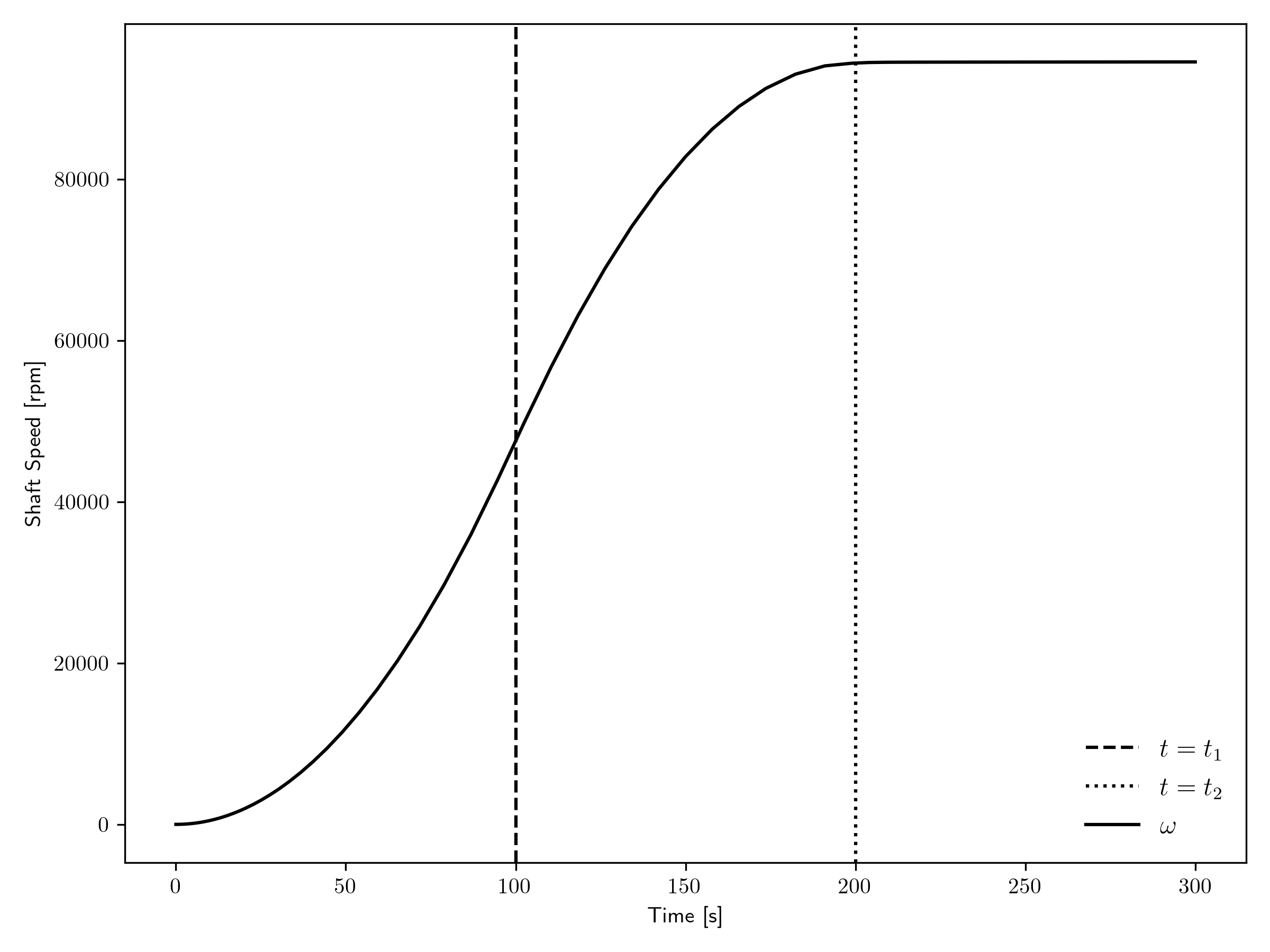
Figure 2: Shaft speed transient for the open cycle.

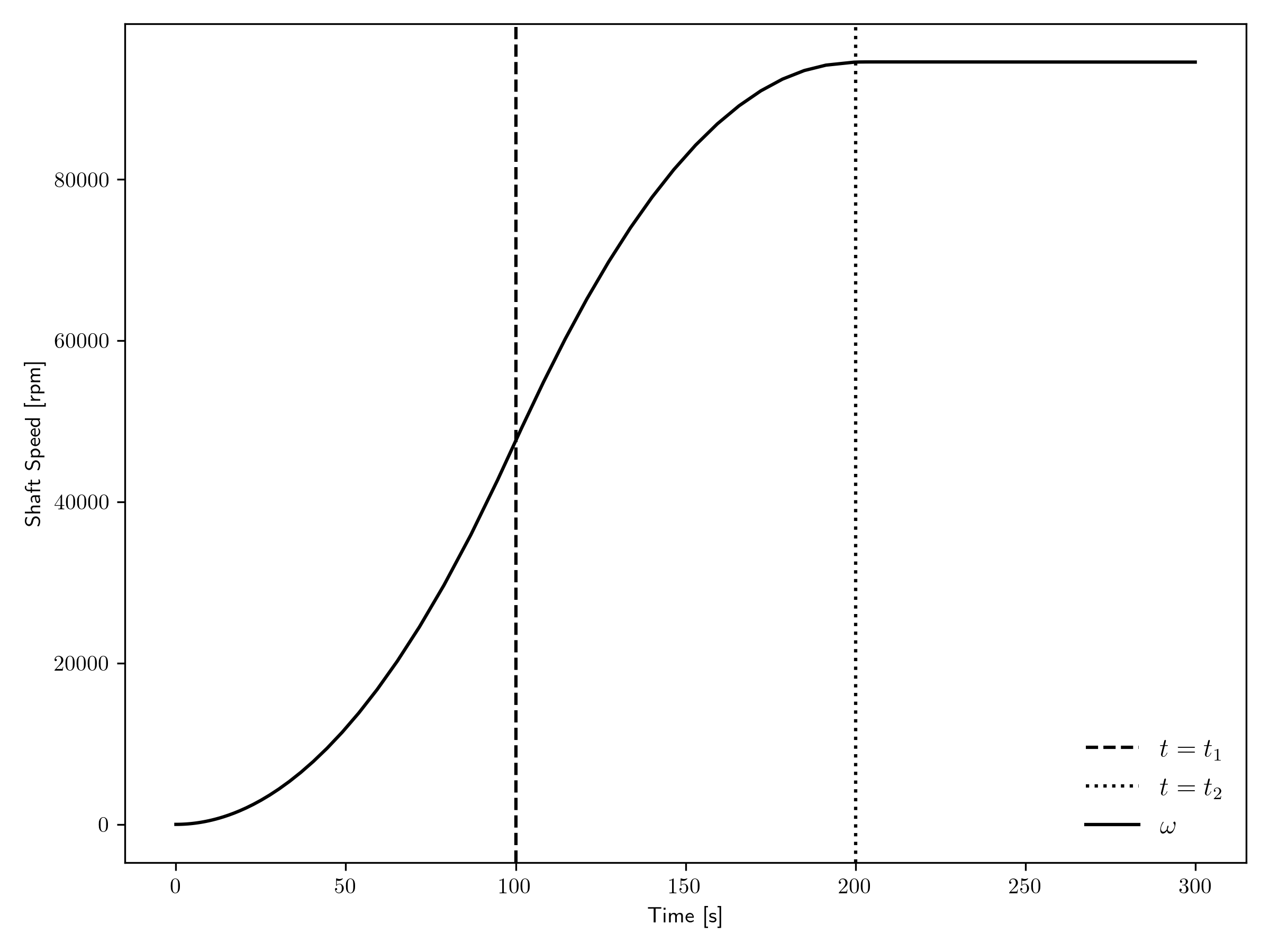
Figure 3: Shaft speed transient for the closed cycle.

Figure 4 and Figure 5 show the mass flow rate transient for the open and closed cycles, respectively. At the beginning of the transient, the mass flow rate is zero, and as the shaft starts spinning, either the compressor or turbine first gets a pressure ratio greater than 1, which allows flow to begin. It can be seen that the mass flow rate is actually slightly negative before the compressor finally activates. Then as the pressure ratios further increase, the mass flow rate increases until it reaches the steady condition.

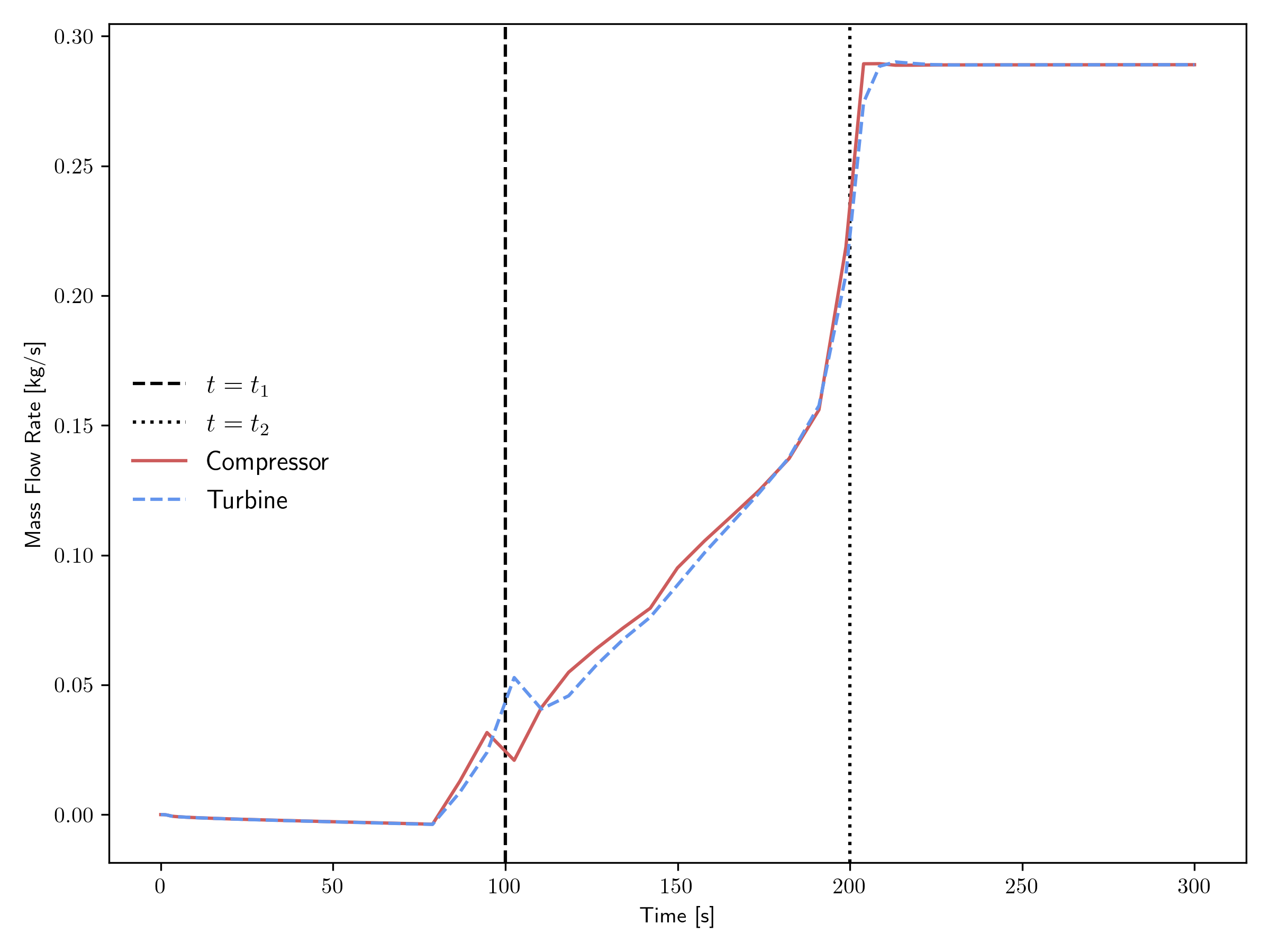
Figure 4: Mass flow rate transient for the open cycle.

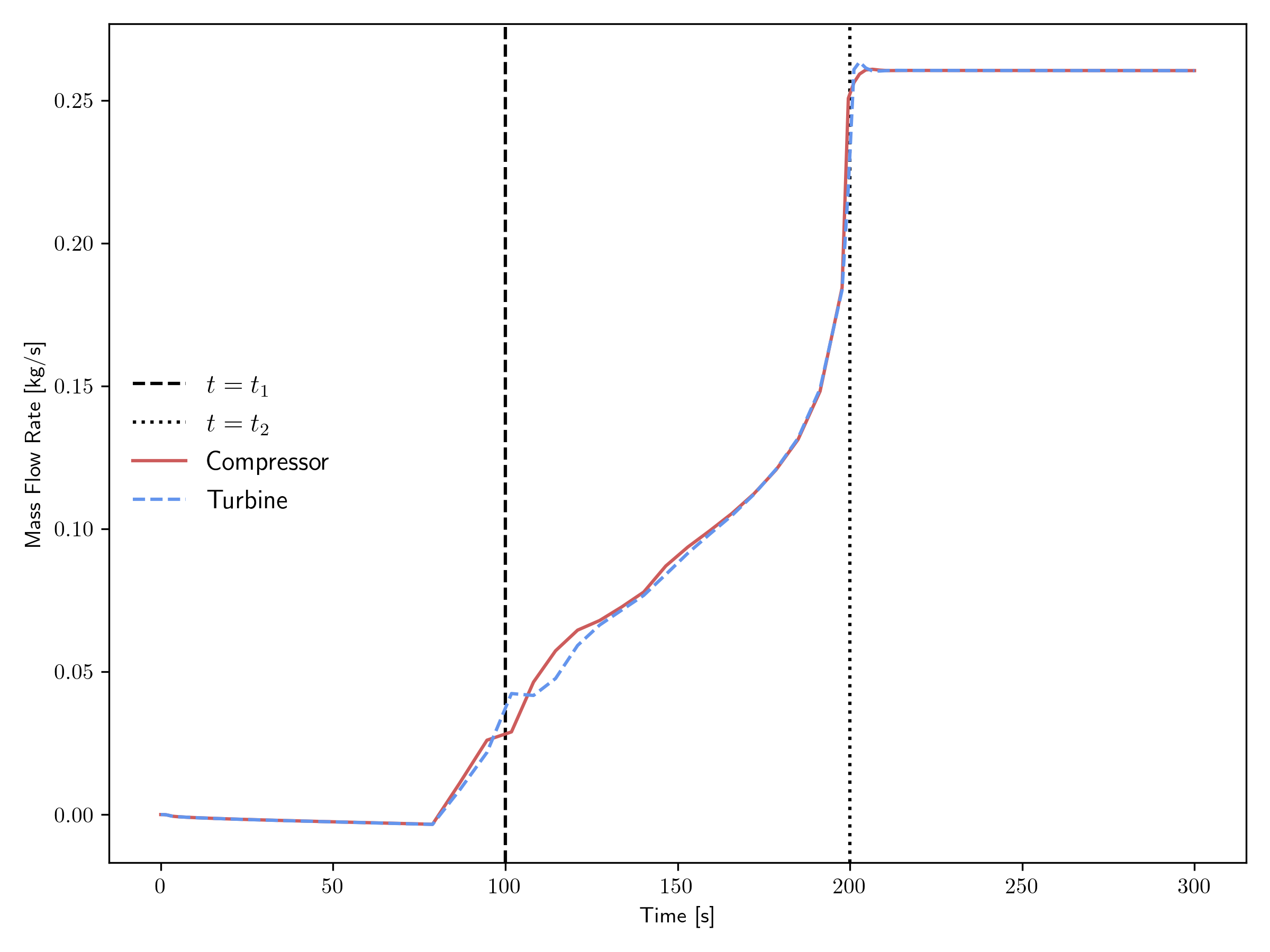
Figure 5: Mass flow rate transient for the closed cycle.

Figure 6 and Figure 7 show the pressure ratio transient for the open and closed cycles, respectively. Recall that this example starts with everything at rest, i.e., there is initially no flow or shaft speed. The motor ramps up the shaft speed to get the compressor working, but only around t=80t = 80 s does the pressure ratio of the compressor and turbine start to exceed 1, which is the point at which flow can start to develop. In this case, the pressure ratio in the compressor exceeds the turbine pressure ratio for the majority of the transient, as the flow and shaft conditions seek to find an equilibrium state, at which the pressure ratios of the compressor and turbine are nearly equal.

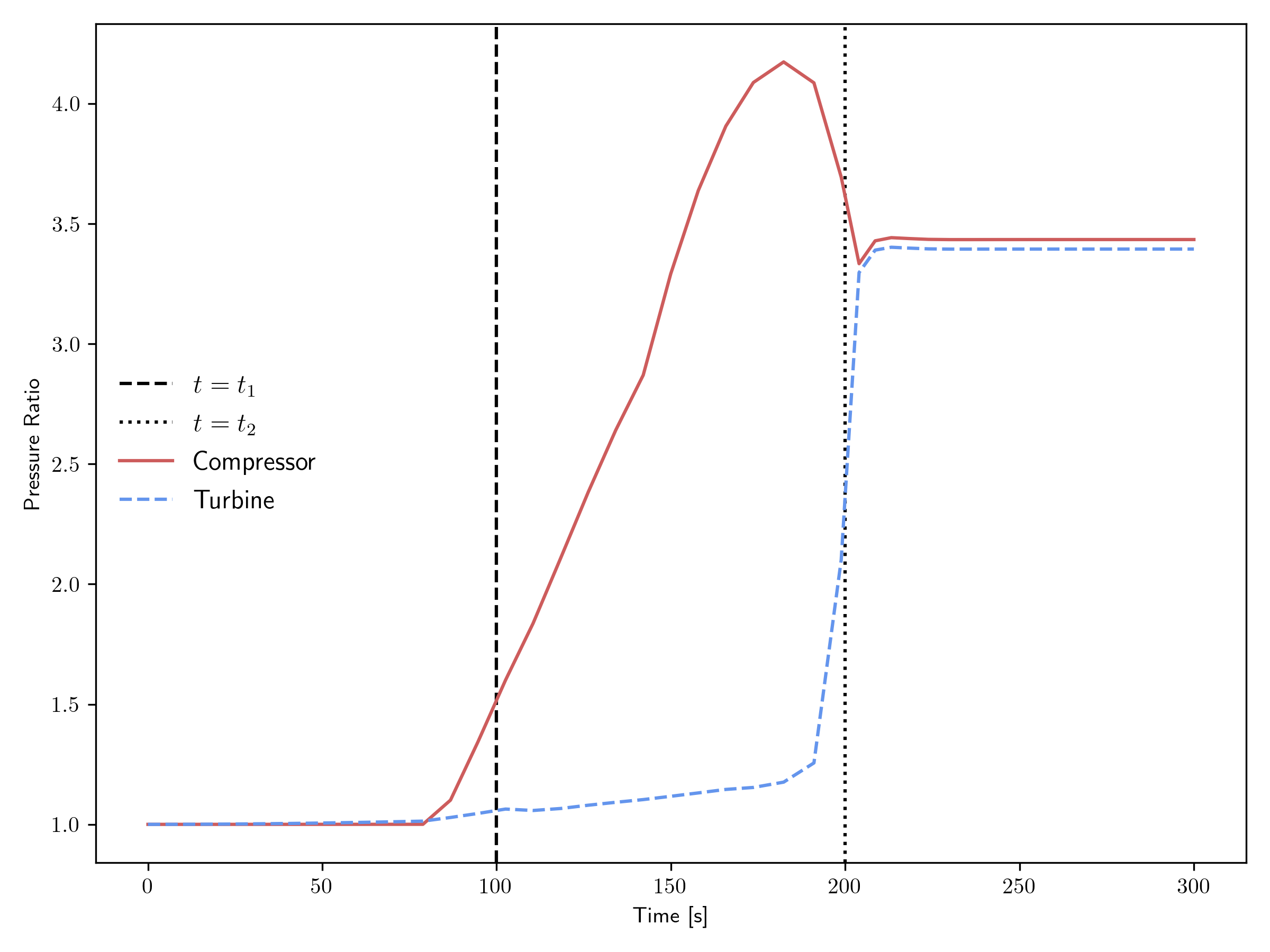
Figure 6: Pressure ratio transient for the open cycle.

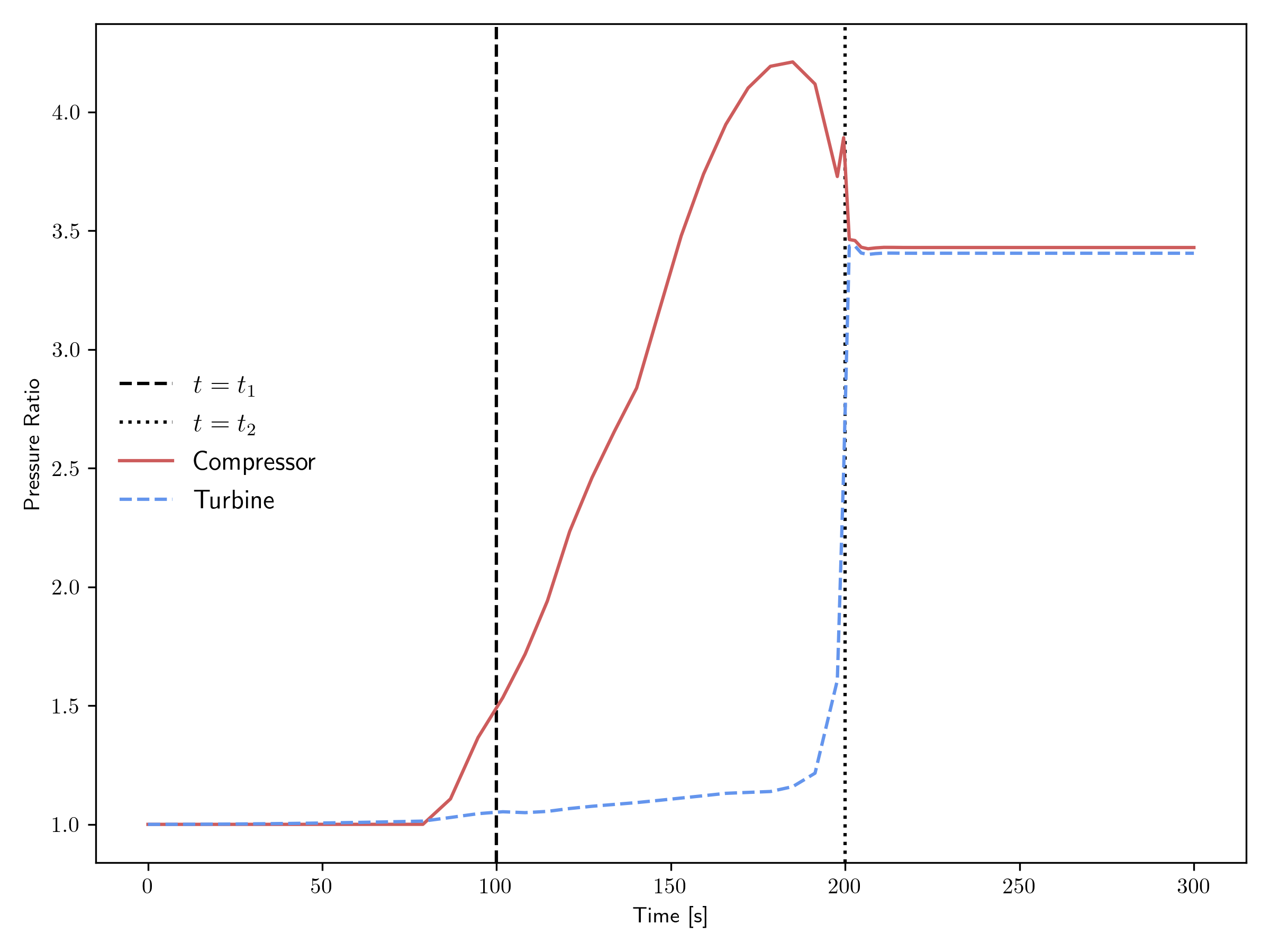
Figure 7: Pressure ratio transient for the closed cycle.

Figure 8 and Figure 9 show the power transient for the open and closed cycles, respectively. Several quantities are included on these plots:

  • Q˙in\dot{Q}_\text{in}, the thermal power provided by the heat source,

  • Q˙out\dot{Q}_\text{out}, the thermal power provided by the heat sink (closed cycle only),

  • W˙gen\dot{W}_\text{gen}, the power taken by the generator (and thus becomes useful electrical power),

  • W˙comp\dot{W}_\text{comp}, the power consumed by the compressor, and

  • W˙turb\dot{W}_\text{turb}, the power provided by the turbine.

Not shown in these plots is the power consumed by the motor, as it dwarfs the other powers shown for the period of the transient where it is most active. In a practical setup, the motor power may be much less and just operates for a much longer period during startup.

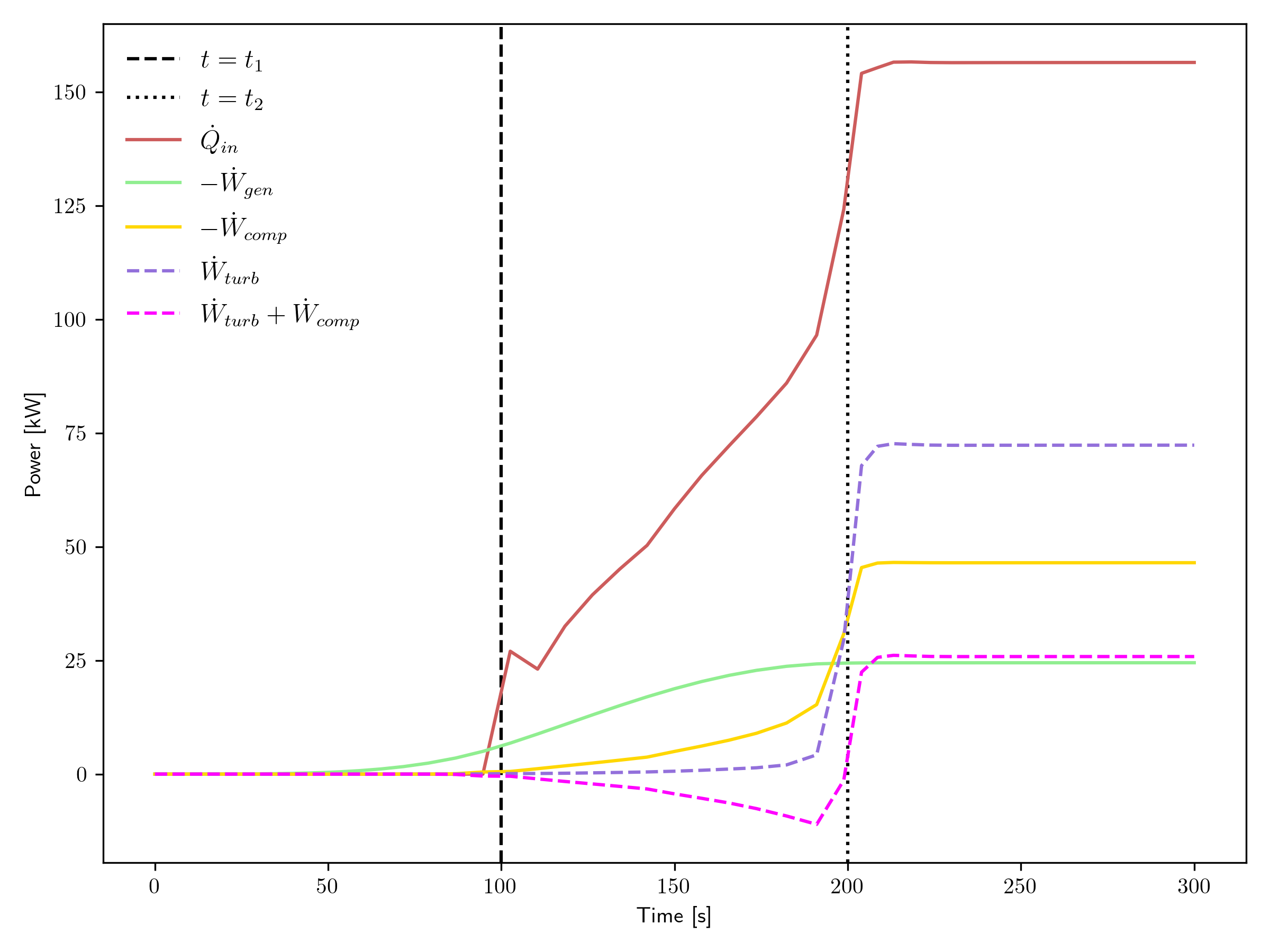
Figure 8: Power transient for the open cycle.

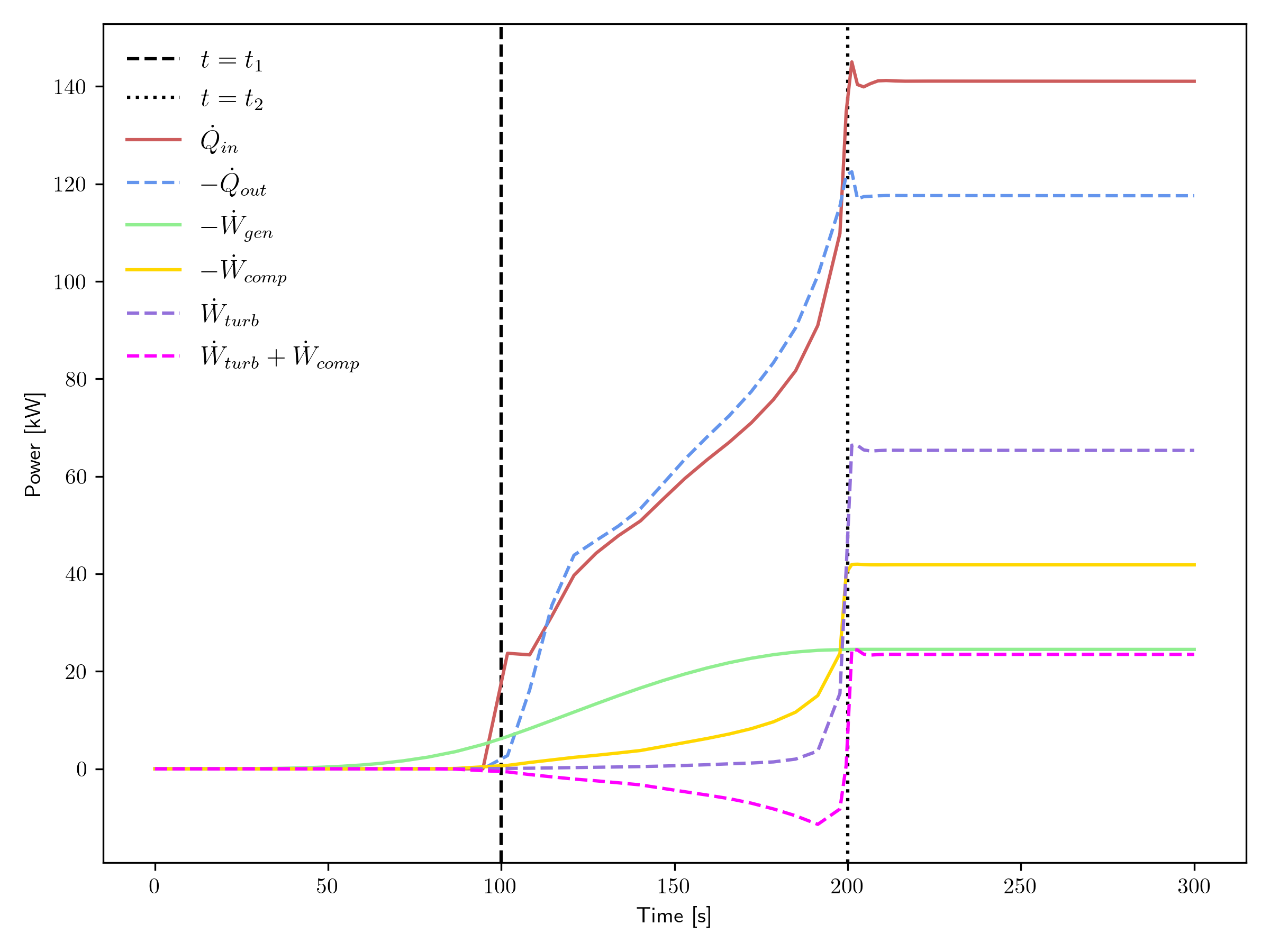
Figure 9: Power transient for the closed cycle.

Comparing the various plots between the open and closed cycles supports the assertion that a closed Brayton cycle approximation can yield very similar results to an open Brayton cycle.

References

  1. Donna Post Guillen and Daniel S. Wendt. Integration of a microturbine power conversion unit in MAGNET. Technical Report INL/EXT-20-57712, Idaho National Laboratory, 8 2020. URL: https://www.osti.gov/biblio/1736010, doi:10.2172/1736010.[BibTeX]