Gaussian Process Surrogate

This example walks through the creation of a few gaussian process surrogates on a simple example system with an analytical solution for comparison. The first surrogate considers a single input parameter to be varied, which lends itself to a simple visual interpretation of the surrogate behavior. The next surrogate extends this idea to two input parameters being modeled. Lastly the full system is modeled with all input parameters, and compared to the analytical solution using sampling. It's recommended users be familiar with the basic surrogate framework, such as Creating a Surrogate Model, Training a Surrogate Model, and Evaluating a Surrogate Model.

Problem Statement

The full order model we wish to emulate with this surrogate is a one-dimensional heat conduction model with four input parameters {k,q,L,T∞}\lbrace k, q, L, T_{\infty} \rbrace.

−kd2Tdx2=q ,x∈[0,L]-k\frac{d^2T}{dx^2} = q \,, \quad x\in[0, L]dTdx∣x=0=0T(x=L)=T∞\begin{aligned} \left.\frac{dT}{dx}\right|_{x=0} &= 0 \\ T(x=L) &= T_{\infty} \end{aligned}

When creating a surrogate using Gaussian Processes, a quantity of interest should be chosen (as opposed to attempting to model T(x)T(x) directly). In this The quantity of interest chosen for this example is the average temperature:

Input Parameters

Table 1:

ParameterSymbolNormalUniform
Conductivitykk∼N(5,2)\sim\mathcal{N}(5, 2)∼U(0,20)\sim\mathcal{U}(0, 20)
Volumetric Heat Sourceqq∼N(10000,500)\sim\mathcal{N}(10000, 500)∼U(7000,13000)\sim\mathcal{U}(7000, 13000)
Domain SizeLL∼N(0.03,0.01)\sim\mathcal{N}(0.03, 0.01)∼U(0,0.1)\sim\mathcal{U}(0, 0.1)
Right Boundary TemperatureT∞T_{\infty}∼N(300,10)\sim\mathcal{N}(300, 10)∼U(270,330)\sim\mathcal{U}(270, 330)

Analytical Solutions

This simple model problem has analytical descriptions for the field temperature and average temperature:

T(x,k,q,L,T∞)=q2k(L2−x2)+T∞Tˉ(k,q,L,T∞)=qL23k+T∞\begin{aligned} T(x,k,q,L,T_{\infty}) &= \frac{q}{2k}\left(L^2 - x^2\right) + T_{\infty} \\ \bar{T}(k,q,L,T_{\infty}) &= \frac{qL^2}{3k} + T_{\infty} \\ \end{aligned}

For that reason Tˉ\bar{T} is chosen as the QoI to be modeled by the surrogate for this example problem. The closed form solution allows for easy comparison between the surrogate and the exact solution.

Setting up a 1D Problem

Problems with a single input variable are a good place to provide insight on Gaussian Process regression. To accomplish this three parameters of our model system are fixed {k=5,L=0.03,T∞=300}\lbrace k=5, L=0.03, T_{\infty}=300 \rbrace, leaving the surrogate to only model the action of varying qq.

6 training values for qq were selected from ∼U(1,10)\sim\mathcal{U}(1, 10) and evaluated using a full model evaluation. The Gaussian Process model was fitted to these data points.

The Gaussian Process was chosen to use a SquaredExponentialCovariance covariance function, using three user selected hyperparameter settings: {σn=1E−3,σf=1,ℓq=0.38971}\lbrace \sigma_n=1E-3, \sigma_f=1 , \ell_q=0.38971 \rbrace. To set up the training for this surrogate we require the standard Trainers block found in all surrogate models in addition to the Gaussian Process specific Covariance block. Hyperparameters vary depending on the covariance function selected, and are therefore specified in the Covariance block.

[Trainers]
  [GP_avg_trainer]
    type = GaussianProcessTrainer
    execute_on = timestep_end
    sampler = train_sample
    response = results/data:avg:value
    covariance_function = 'rbf'
    standardize_params = 'true' #Center and scale the training params
    standardize_data = 'true' #Center and scale the training data
  []
[]

[Covariance]
  [rbf]
    type = SquaredExponentialCovariance
    signal_variance = 1 #Use a signal variance of 1 in the kernel
    noise_variance = 1e-3 #A small amount of noise can help with numerical stability
    length_factor = '0.38971' #Select a length factor for each parameter (k and q)
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_1D.i)

Creation of the Surrogate block follows the standard procedure laid out for other surrogate models.

[Surrogates]
  [gauss_process_avg]
    type = GaussianProcessSurrogate
    trainer = 'GP_avg_trainer'
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_1D.i)

One advantage of Gaussian Process surrogates is the ability to provide an model for uncertainty. To output this data the standard EvaluateSurrogate reporter is used with specification of "evaluate_std", which also outputs the standard deviation of the surrogate at the evaluation point.

[Reporters]
  [results]
    type = StochasticReporter
  []
  [cart_avg]
    type = EvaluateSurrogate
    model = gauss_process_avg
    sampler = cart_sample
    evaluate_std = 'true'
    parallel_type = ROOT
    execute_on = final
  []
  [train_avg]
    type = EvaluateSurrogate
    model = gauss_process_avg
    sampler = train_sample
    evaluate_std = 'true'
    parallel_type = ROOT
    execute_on = final
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_1D.i)

The Gaussian Process surrogate model can only be evaluated at discrete points in the parameter space, so if we wish to visualize the response model fine sampling is required. To accomplish this sampling a CartesianProductSampler evaluates the model for 100 evenly spaced qq values in [9000,11000][9000,11000]. This sampling is plotted below in Figure 1 (space between the 100 sampled points are filled by simple linear interpolation, so strictly speaking the plot is not exactly the model)

[Samplers]
  [train_sample]
    type = MonteCarlo
    num_rows = 6
    distributions = 'q_dist'
    execute_on = PRE_MULTIAPP_SETUP
  []
  [cart_sample]
    type = CartesianProduct
    linear_space_items = '9000 20 100'
    execute_on = initial
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_1D.i)

Figure 1: Surrogate model for 1D problem Tˉ(q)\bar{T}(q) using fixed (user specified) hyperparameters.

Figure 1 demonstrates some basic principles of the gaussian process surrogate for this covariance function. Near training points (red + markers), the uncertainty in the model trends towards the measurement noise σn\sigma_n. The model function is smooth and infinitely differentiable. As we move away from the data points the model tends to just predict the mean of the training data, particularly noticeable in the extrapolation regions of the graph.

However, given that in this scenario we know the model should be a simple linear fit, we may conclude that this fit should be better. To achieve a better fit the model needs to be adjusted, specifically better hyperparameters for the covariance function likely need to be tested. For many hyperparameters this can be accomplished automatically by the system. To enable this specify the tuned hyperparameters using "tune_parameters" in the trainer. Tuning bounds can be placed using "tuning_min" and "tuning_max".

[Trainers]
  [GP_avg_trainer]
    type = GaussianProcessTrainer
    execute_on = timestep_end
    response = results/data:avg:value
    covariance_function = 'rbf'
    standardize_params = 'true' #Center and scale the training params
    standardize_data = 'true' #Center and scale the training data
    sampler = train_sample
    tune_parameters = 'rbf:signal_variance rbf:length_factor'
    tuning_min = ' 1e-9 1e-9'
    tuning_max = ' 1e16  1e16'
    num_iters = 10000
    batch_size = 6
    learning_rate = 0.0005
    show_every_nth_iteration = 1
  []
[]

[Covariance]
  [rbf]
    type = SquaredExponentialCovariance
    signal_variance = 1 #Use a signal variance of 1 in the kernel
    noise_variance = 1e-3 #A small amount of noise can help with numerical stability
    length_factor = '0.38971' #Select a length factor for each parameter (k and q)
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_1D_tuned.i)

To demonstrate the importance of hyperparameter tuning, the same data set was then used to train a surrogate with hyperparameter auto-tuning enabled. In this mode the system attempts to learn an optimal hyperparameter configuration to maximize the likelihood of observing the data from the fitted model. The results shown in Figure 2 is a nearly linear fit, with very little uncertainty in the fit, which is what we expect from the analytical form.

Figure 2: Surrogate model for 1D problem Tˉ(q)\bar{T}(q) using tuned hyperparameters.

Inspection of the final hyperparameter values after tuning gives {σn=3.79E−6,σf=3.87,ℓq=4.59}\lbrace \sigma_n=3.79E-6, \sigma_f=3.87 , \ell_q=4.59 \rbrace, the significant increase in the length scale ℓq\ell_q is a primary factor in the improved fit.

Setting up a 2D Problem

Next the idea is extended to two input dimensions and attempt to model the QoI behavior due to varying kk and qq, while fixing values of {L=0.03,T∞=300}\lbrace L=0.03, T_{\infty}=300 \rbrace.

Due to the increased dimensionality, 50 training samples were selected from q∈[9000,11000]q \in [9000,11000] and k∈[1,10]k \in [1,10]. An extra hyperparameter ℓk\ell_k is also added to the set of hyperparameters to be tuned.

[Samplers]
  [train_sample]
    type = MonteCarlo
    num_rows = 50
    distributions = 'k_dist q_dist'
    execute_on = PRE_MULTIAPP_SETUP
  []
  [cart_sample]
    type = CartesianProduct
    linear_space_items = '1 0.09 10
                          9000 20 10 '
    execute_on = initial
  []
[]

[Trainers]
  [GP_avg_trainer]
    type = GaussianProcessTrainer
    execute_on = timestep_end
    covariance_function = 'rbf'
    standardize_params = 'true' #Center and scale the training params
    standardize_data = 'true' #Center and scale the training data
    sampler = train_sample
    response = results/data:avg:value
    tune_parameters = 'rbf:signal_variance rbf:length_factor'
    tuning_min = '1e-9 1e-9'
    tuning_max = '1e16  1e16'
    batch_size = 50
    num_iters = 5000
    learning_rate = 5e-3
  []
[]

[Covariance]
  [rbf]
    type = SquaredExponentialCovariance
    signal_variance = 1 #Use a signal variance of 1 in the kernel
    noise_variance = 1e-3 #A small amount of noise can help with numerical stability
    length_factor = '0.38971 0.38971' #Select a length factor for each parameter (k and q)
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/gaussian_process_uniform_2D_tuned.i)

As was done in the 1D case above, first the surrogate was fitted using fixed hyperparameters {σn=1E−3,σf=10,ℓq=0.38971,ℓk=0.38971}\lbrace \sigma_n=1E-3, \sigma_f=10, \ell_q=0.38971 , \ell_k=0.38971 \rbrace. The QoI surface is shown in Figure 3, with the color map corresponding to the surrogate model's uncertainty at that point. As was the case in the 1D mode, uncertainty is highest at points furthest from training data points, and the overall response deviates strongly from the expected qk\frac{q}{k} behavior predicted.

Figure 3: Surrogate model for 2D problem Tˉ(q,k)\bar{T}(q,k) using fixed hyperparameters.

Hyperparameter tuning is then enabled by setting "tune_parameters". Figure 4 shows the fit with automatically tuned hyperparameters using the same data set. This results in a fit that much better captures the qk\frac{q}{k} nature of the QoI response, with "high" uncertainty occurring primarily in extrapolation zones.

Figure 4: Surrogate model for 2D problem Tˉ(q,k)\bar{T}(q,k) using tuned hyperparameters.

Full 4D Problem

This idea is then extended naturally to the full problem in which the parameter set {k,q,L,T∞}\lbrace k, q, L, T_{\infty} \rbrace is modeled. Training occurs using 500500 training points in. Evaluation occurs by sampling the surrogate 1000010000 times with perturbed inputs, with results shown in histogram form in Figure 5. While the 1000010000 evaluation points are sampled from the normal distribution in Table 1,the 500500 training data points are sampled from the uniform distributions. Sampling the training data from the normal distribution can result in an imbalance of data points near the mean, causing poor performance in outlying regions. The training and evaluation inputs are (contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/GP_normal_mc.i) and (contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/GP_normal.i) respectively.

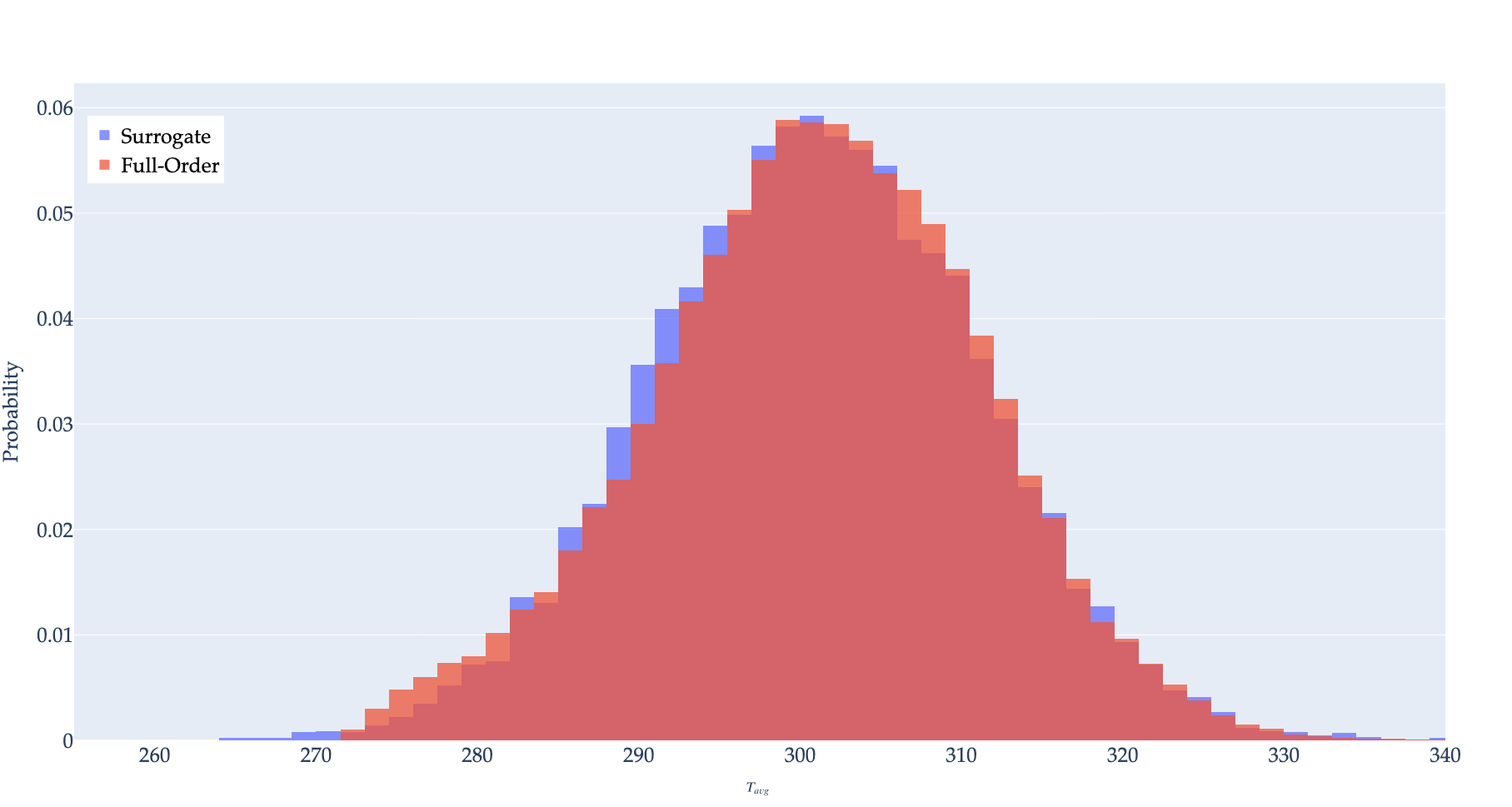
Figure 5: Histogram of 1000010000 samples of surrogate Tˉ(q,k,L,T∞)\bar{T}(q,k,L,T_{\infty}) compared to exact.

To showcase more optimization options available in GaussianProcessTrainer, we used Adam for fitting the length scales and signal variance in this process. The parameters for Adam (number of iterations, learning rate, etc.) can be set using the following syntax:

[Trainers]
  [GP_avg]
    type = GaussianProcessTrainer
    execute_on = timestep_end
    covariance_function = 'rbf'
    standardize_params = 'true' #Center and scale the training params
    standardize_data = 'true' #Center and scale the training data
    sampler = sample
    response = results/data:avg:value
    tune_parameters = 'rbf:signal_variance rbf:length_factor'
    tuning_min = ' 1e-9 1e-3'
    tuning_max = ' 100  100'
    num_iters = 200
    learning_rate = 0.005
  []
[]
(contrib/moose/modules/stochastic_tools/examples/surrogates/gaussian_process/GP_normal_mc.i)