Beams

Small strain Timoshenko beam bending

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam has a cross section area of 0.554 m2{m}^2, moment of inertia about Y and Z axis of 0.0142 m4{m}^4, Young's modulus of elasticity of 2.6 N/m2{m}^2, poisson's ratio of 0.3, shear modulus of 1 N/m2{m}^2 and shear coefficient of 0.85. A point load of magnitude 1×\times10−^-4^4 N is applied at the free end of the cantilever beam in Y-direction.

# Test for small strain timoshenko beam bending in y direction

# A unit load is applied at the end of a cantilever beam of length 4m.
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 2.60072400269
# Shear modulus (G) = 1.00027846257
# Poisson's ratio (nu) = 0.3
# Shear coefficient (k) = 0.85
# Cross-section area (A) = 0.554256
# Iy = 0.0141889 = Iz
# Length = 4 m

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 204.3734

# The small deformation analytical deflection of the beam is given by
# delta = PL^3/3EI * (1 + 3.0 / alpha) = 5.868e-4 m

# Using 10 elements to discretize the beam element, the FEM solution is 5.852e-2m.
# This deflection matches the FEM solution given in Prathap and Bhashyam (1982).

# References:
# Prathap and Bhashyam (1982), International journal for numerical methods in engineering, vol. 18, 195-210.
# Note that the force is scaled by 1e-4 compared to the reference problem.

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
  xmin = 0.0
  xmax = 4.0
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = ConstantRate
    variable = disp_y
    boundary = right
    rate = 1.0e-4
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]
[Executioner]
  type = Transient
  solve_type = NEWTON
  line_search = 'none'
  nl_max_its = 15
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-10

  dt = 1
  dtmin = 1
  end_time = 2
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 2.60072400269
    poissons_ratio = 0.3
    shear_coefficient = 0.85
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 0.554256
    Ay = 0.0
    Az = 0.0
    Iy = 0.0141889
    Iz = 0.0141889
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
[]

[Outputs]
  exodus = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/static/timoshenko_small_strain_y.i)

Results

For this beam, the dimensionless parameter alpha is given by: alpha=kAGL2EI=204.3734alpha = \frac {kAGL^2}{EI} = 204.3734 The value of alpha is not high enough for the beam to behave like a thin beam where shear effects are not significant. Hence, the shear effects are considered and the small deformation analytical deflection of a cantilever beam is given by: Δ=PL33EI  (1+3alpha)=5.868×10−2m\Delta = \frac {PL^3}{3EI} \; (1 + \frac {3}{alpha}) = 5.868 \times 10^{-2} m

The deflection obtained from MOOSE using 10 elements is 5.852×\times10−^-2^2 m shown in Figure 1.

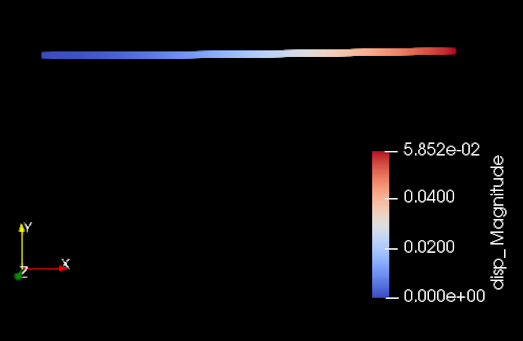
Figure 1: Displacement of the Timoshenko beam in bending.

Small strain Euler beam bending

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam has a cross section area of 0.554 m2{m}^2, moment of inertia about Y and Z axis of 0.0142 m4{m}^4, Young's modulus of elasticity of 2.6 N/m2{m}^2, poisson's ratio of -0.99, shear modulus of 1×\times104^4 N/m2{m}^2 and shear coefficient of 0.85. A point load of magnitude 1×\times10−^-4^4 N is applied at the free end of the cantilever beam in Y-direction.

# Test for small strain Euler beam bending in y direction

# A unit load is applied at the end of a cantilever beam of length 4m.
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 2.60072400269
# Shear modulus (G) = 1.0e4
# Poisson's ratio (nu) = -0.9998699638
# Shear coefficient (k) = 0.85
# Cross-section area (A) = 0.554256
# Iy = 0.0141889 = Iz
# Length = 4 m

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 2.04e6

# The small deformation analytical deflection of the beam is given by
# delta = PL^3/3EI * (1 + 3.0 / alpha) = PL^3/3EI = 5.78e-2 m

# Using 10 elements to discretize the beam element, the FEM solution is 5.766e-2 m.
# The ratio beam FEM solution and analytical solution is 0.998.

# References:
# Prathap and Bhashyam (1982), International journal for numerical methods in engineering, vol. 18, 195-210.
# Note that the force is scaled by 1e-4 compared to the reference problem.

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
  xmin = 0.0
  xmax = 4.0
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = ConstantRate
    variable = disp_y
    boundary = right
    rate = 1.0e-4
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]
[Executioner]
  type = Transient
  solve_type = NEWTON
  line_search = 'none'
  nl_max_its = 15
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-10

  dt = 1
  dtmin = 1
  end_time = 2
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 2.60072400269
    poissons_ratio = -0.9998699638
    shear_coefficient = 0.85
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 0.554256
    Ay = 0.0
    Az = 0.0
    Iy = 0.0141889
    Iz = 0.0141889
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
[]

[Outputs]
  exodus = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/static/euler_small_strain_y.i)

Results

For this beam, the dimensionless parameter alpha is given by: alpha=kAGL2EI=2.04×106alpha = \frac {kAGL^2}{EI} = 2.04 \times 10^6 Since the value of alpha is quite high, the beam behaves like a thin beam where shear effects are not significant. Hence, the small deformation analytical deflection of a cantilever beam is given by: Δ=PL33EI  (1+3alpha)=PL33EI  =5.78×10−2m\Delta = \frac {PL^3}{3EI} \; (1 + \frac {3}{alpha}) = \frac {PL^3}{3EI} \; =5.78 \times 10^{-2} m

The deflection obtained from MOOSE using 10 elements is 5.766×\times10−^-2^2 m shown in Figure 2. The ratio beam FEM solution and analytical solution is 0.998.

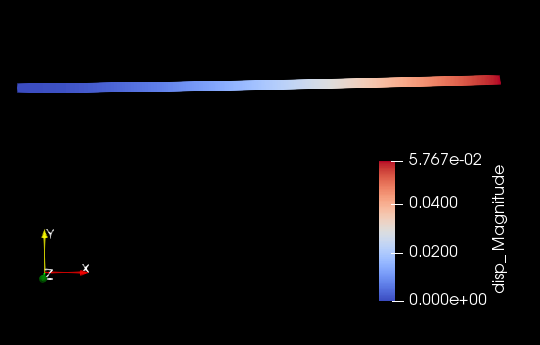
Figure 2: Displacement of the Euler beam in bending.

Small strain Euler beam axial loading

A pipe 5 feet (60 inches) long having an internal diameter of 8 inches and outer diameter of 10 inches is modeled using beam elements in MOOSE. The Young's modulus of elasticity of the pipe is 30×\times106^6 lb/in2{in}^2, the shear modulus is 11.54×\times106^6 lb/in2{in}^2 and poisson's ratio is 0.3. The pipe is fixed at one end and an axial load of 50000 lb is applied at the other end.

# Test for small strain Euler beam axial loading in x direction.

# Modeling a pipe with an OD of 10 inches and ID of 8 inches
# The length of the pipe is 5 feet (60 inches) and E = 30e6
# G = 11.5384615385e6 with nu = 0.3
# The applied axial load is 50000 lb which results in a
# displacement of 3.537e-3 inches at the end

# delta = PL/AE = 50000 * 60 / pi (5^2 - 4^2) * 30e6 = 3.537e-3

# In this analysis the applied force is used as a BC

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
  xmin = 0.0
  xmax = 60.0
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_x2]
    type = ConstantRate
    variable = disp_x
    boundary = right
    rate = 50000.0
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]
[Executioner]
  type = Transient
  solve_type = PJFNK
  line_search = 'none'
  nl_max_its = 15
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-8

  dt = 1
  dtmin = 1
  end_time = 2
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    shear_coefficient = 1.0
    youngs_modulus = 30e6
    poissons_ratio = 0.3
    block = 0
    outputs = exodus
    output_properties = 'material_stiffness material_flexure'
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 28.274
    Ay = 0.0
    Az = 0.0
    Iy = 1.0
    Iz = 1.0
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
    outputs = exodus
    output_properties = 'forces moments'
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '60.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '60.0 0.0 0.0'
    variable = disp_y
  [../]
  [./forces_x]
    type = PointValue
    point = '60.0 0.0 0.0'
    variable = forces_x
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/static/euler_pipe_axial_force.i)

Results

The analytical displacement at the end is given by: Δ=PLAE=3.537×10−3in\Delta = \frac {PL}{AE} = 3.537 \times 10^{-3} in

The displacement at the end obtained from the MOOSE using 10 elements is 3.537×\times10−^-3^3 in as shown in Figure 3.

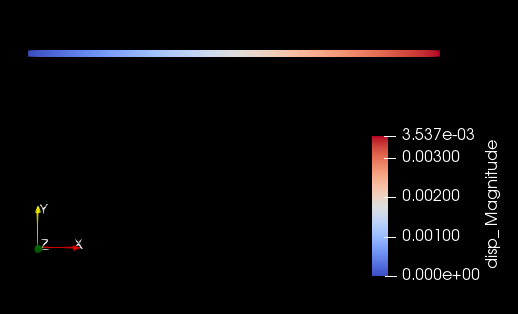
Figure 3: Displacement of the Euler beam under axial load.

Large strain/large rotation of cantilever beam

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam has a cross section area of 1 m2{m}^2, moment of inertia about Y and Z axis of 0.16 m4{m}^4, Young's modulus of elasticity of 1×\times104^4 N/m2{m}^2, poisson's ratio of -0.99, shear modulus of 1×\times108^8 N/m2{m}^2 and shear coefficient of 1. A point load of magnitude 300 N is applied at the free end of the cantilever beam in Y-direction.

# Large strain/large rotation cantilever beam test

# A 300 N point load is applied at the end of a 4 m long cantilever beam.
# Young's modulus (E) = 1e4
# Shear modulus (G) = 1e8
# shear coefficient (k) = 1.0
# Poisson's ratio (nu) = -0.99995
# Area (A) = 1.0
# Iy = Iz = 0.16

# The dimensionless parameter alpha = kAGL^2/EI = 1e6
# Since the value of alpha is quite high, the beam behaves like
# a thin beam where shear effects are not significant.

# Beam deflection:
# small strain+rot = 3.998 m (exact 4.0)
# large strain + small rotation = -0.05 m in x and 3.74 m in y
# large rotations + small strain = -0.92 m in x and 2.38 m in y
# large rotations + large strain = -0.954 m in x and 2.37 m in y (exact -1.0 m in x and 2.4 m in y)

# References:
# K. E. Bisshopp and D.C. Drucker, Quaterly of Applied Mathematics, Vol 3, No. 3, 1945.

[Mesh]
  type = FileMesh
  file = beam_finite_rot_test_2.e
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = 1
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = 1
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = 1
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = 1
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = 1
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = 1
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = UserForcingFunctionNodalKernel
    variable = disp_y
    boundary = 2
    function = force
  [../]
[]

[Functions]
  [./force]
    type = PiecewiseLinear
    x = '0.0 2.0  8.0'
    y = '0.0 300.0 300.0'
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  line_search = 'none'
  petsc_options = '-snes_ksp_ew'
  petsc_options_iname = '-ksp_gmres_restart -pc_type -pc_hypre_type -pc_hypre_boomeramg_max_iter'
  petsc_options_value = '201                hypre     boomeramg     4'
  nl_max_its = 50
  nl_rel_tol = 1e-9
  nl_abs_tol = 1e-7
  l_max_its = 50
  dt = 0.05
  end_time = 2.1
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 1e4
    poissons_ratio = -0.99995
    shear_coefficient = 1.0
    block = 1
  [../]
  [./strain]
    type = ComputeFiniteBeamStrain
    block = '1'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 1.0
    Ay = 0.0
    Az = 0.0
    Iy = 0.16
    Iz = 0.16
    y_orientation = '0.0 1.0 0.0'
    large_strain = true
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 1
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
  [./rot_z]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = rot_z
  [../]
[]

[Outputs]
  exodus = true
  perf_graph = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/static/euler_finite_rot_y.i)

Results

For this beam, the dimensionless parameter alpha is given by: alpha=kAGL2EI=1×106alpha = \frac {kAGL^2}{EI} = 1\times 10^6 Since, the value of alpha is quite high, the beam behaves like a thin beam where shear effects are not significant. The analytical solution for the displacements due to large rotations and large strain of the cantilever beam in X and Y direction is -1 m and 2.4 m respectively (BISSHOPP and DRUCKER (1945)).

The displacement at the free end of the cantilever beam obtained from the MOOSE is -0.954 m in X direction as shown in Figure 4 and 2.37 m in Y direction as shown in Figure 5.

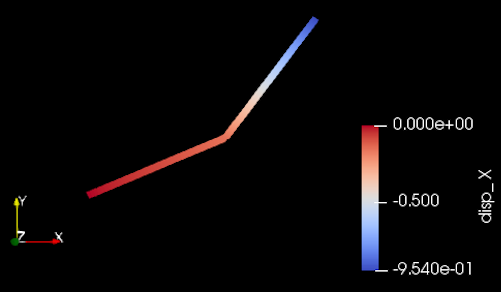
Figure 4: Displacement of the cantilever beam with large strain and rotation in X direction

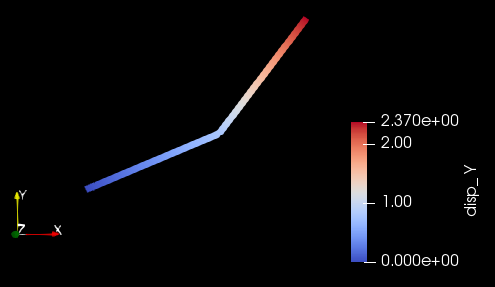
Figure 5: Displacement of the cantilever beam with large strain and rotation in Y direction

Torsion

A 1D cantilever beam of 1 m is modeled using beam elements in MOOSE. The beam has a cross section area of 0.5 m2{m}^2, moment of inertia about Y and Z axis of 1×\times10−^-5^5 m4{m}^4, Young's modulus of elasticity of 2×\times109^9 N/m2{m}^2, poisson's ratio of 0.3 and shear coefficient of 1. A torsion of magnitude 5 N/m is applied at the free end of the cantilever beam.

# Torsion test with automatically calculated Ix

# A beam of length 1 m is fixed at one end and a moment  of 5 Nm
# is applied along the axis of the beam.
# G = 7.69e9
# Ix = Iy + Iz = 2e-5
# The axial twist at the free end of the beam is:
# phi = TL/GIx = 3.25e-4

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
  xmin = 0.0
  xmax = 1.0
  displacements = 'disp_x disp_y disp_z'
[]

[Physics/SolidMechanics/LineElement/QuasiStatic]
  [./block_all]
    add_variables = true
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'

    # Geometry parameters
    area = 0.5
    Iy = 1e-5
    Iz = 1e-5

    y_orientation = '0.0 1.0 0.0'

    block = 0
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = ConstantRate
    variable = rot_x
    boundary = right
    rate = 5.0
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]
[Executioner]
  type = Transient
  solve_type = PJFNK
  line_search = 'none'
  nl_max_its = 15
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-8

  dt = 1
  dtmin = 1
  end_time = 2
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 2.0e9
    poissons_ratio = 0.3
    shear_coefficient = 1.0
    block = 0
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '1.0 0.0 0.0'
    variable = rot_x
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/static/torsion_1.i)

Results

The analytical solution for the axial twist at the free end of the beam is given by: ϕ=TLGIx=3.25×10−4rad\phi = \frac {TL}{GI_{x}} = 3.25\times 10^{-4} rad where,Ix=Iy+Iz=2×10−5m4where, I_{x} = I_{y} + I_{z} = 2\times 10^{-5} m^4

The rotation at the free end of the beam obtained in MOOSE is 3.2×\times10−^-4^4 rad, as shown in Figure 6.

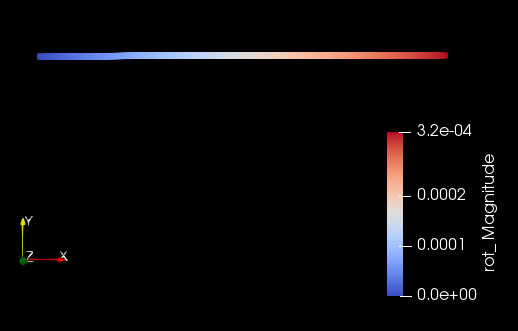
Figure 6: Rotation of the beam due to torsion.

Small strain Euler beam vibration

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam has a cross section area of 0.01 m2{m}^2, moment of inertia about Y and Z axis of 1×\times10−^-4^4 m4{m}^4, Young's modulus of elasticity of 1×\times104^4 N/m2{m}^2, poisson's ratio of -0.99, density of 1 kg/m3{m}^3, shear modulus of 4×\times107^7 N/m2{m}^2 and shear coefficient of 1. An impulse load with a peak value of 0.01 N at 0.05 s, as shown in Figure 7, is applied at the free end of the beam in Y direction. The Newmark time integration parameters used in the problem correspond to the Newmark's average acceleration method, i.e., beta=0.25 and gamma=0.5.

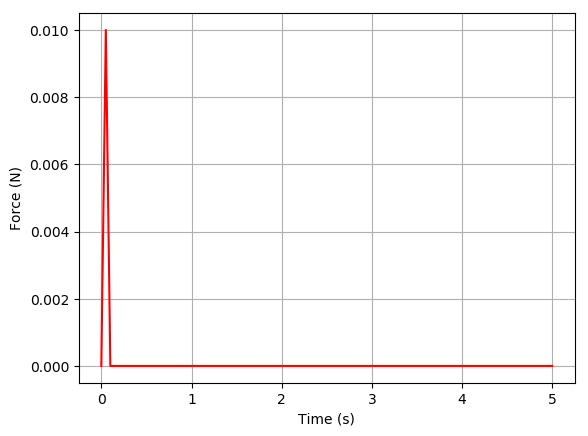
Figure 7: Impulse load pattern applied at the free end of the beam.

# Test for small strain euler beam vibration in y direction

# An impulse load is applied at the end of a cantilever beam of length 4m.
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 1e4
# Shear modulus (G) = 4e7
# Shear coefficient (k) = 1.0
# Cross-section area (A) = 0.01
# Iy = 1e-4 = Iz
# Length (L)= 4 m
# density (rho) = 1.0

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 6.4e6
# Therefore, the beam behaves like a Euler-Bernoulli beam.

# The theoretical first and third frequencies of this beam are:
# f1 = 1/(2 pi) * (3.5156/L^2) * sqrt(EI/rho)
# f2 = 6.268 f1

# This implies that the corresponding time period of this beam are 2.858 s and 0.455s

# The FEM solution for this beam with 10 element gives time periods of 2.856 s and 0.4505s with a time step of 0.01.
# A smaller time step is required to obtain a closer match for the lower time periods/higher frequencies.
# A higher time step of 0.05 is used in this test to reduce testing time.

# The time history from this analysis matches with that obtained from Abaqus.

# Values from the first few time steps are as follows:
# time       disp_y            vel_y            accel_y
# 0     0.0                  0.0                0.0
# 0.05  0.0016523559162602   0.066094236650407  2.6437694660163
# 0.1   0.0051691308901533   0.07457676230532  -2.3044684398197
# 0.15  0.0078956772343372   0.03448509146203   4.7008016060883
# 0.2   0.0096592517031463   0.03605788729033  -0.63788977295649
# 0.25  0.011069233444348    0.020341382357756  0.0092295756535376

[Mesh]
  type = GeneratedMesh
  xmin = 0.0
  xmax = 4.0
  dim = 1
  nx = 10
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[AuxVariables]
  [./vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
[]

[AuxKernels]
  [./accel_x]
    type = NewmarkAccelAux
    variable = accel_x
    displacement = disp_x
    velocity = vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_x]
    type = NewmarkVelAux
    variable = vel_x
    acceleration = accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_y]
    type = NewmarkAccelAux
    variable = accel_y
    displacement = disp_y
    velocity = vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_y]
    type = NewmarkVelAux
    variable = vel_y
    acceleration = accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_z]
    type = NewmarkAccelAux
    variable = accel_z
    displacement = disp_z
    velocity = vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_z]
    type = NewmarkVelAux
    variable = vel_z
    acceleration = accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_x]
    type = NewmarkAccelAux
    variable = rot_accel_x
    displacement = rot_x
    velocity = rot_vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_x]
    type = NewmarkVelAux
    variable = rot_vel_x
    acceleration = rot_accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_y]
    type = NewmarkAccelAux
    variable = rot_accel_y
    displacement = rot_y
    velocity = rot_vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_y]
    type = NewmarkVelAux
    variable = rot_vel_y
    acceleration = rot_accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_z]
    type = NewmarkAccelAux
    variable = rot_accel_z
    displacement = rot_z
    velocity = rot_vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_z]
    type = NewmarkVelAux
    variable = rot_vel_z
    acceleration = rot_accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = UserForcingFunctionNodalKernel
    variable = disp_y
    boundary = right
    function = force
  [../]
[]

[Functions]
  [./force]
    type = PiecewiseLinear
    x = '0.0 0.05 0.1 10.0'
    y = '0.0 0.01  0.0  0.0'
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]

[Executioner]
  type = Transient
  solve_type = NEWTON

  dt = 0.05
  end_time = 5.0
  timestep_tolerance = 1e-6
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
  [./inertial_force_x]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 0
    variable = disp_x
  [../]
  [./inertial_force_y]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 1
    variable = disp_y
  [../]
  [./inertial_force_z]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 2
    variable = disp_z
  [../]
  [./inertial_force_rot_x]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 3
    variable = rot_x
  [../]
  [./inertial_force_rot_y]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 4
    variable = rot_y
  [../]
  [./inertial_force_rot_z]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 0.01
    Iy = 1e-4
    Iz = 1e-4
    Ay = 0.0
    Az = 0.0
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 1.0e4
    poissons_ratio = -0.999875
    shear_coefficient = 1.0
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 0.01
    Ay = 0.0
    Az = 0.0
    Iy = 1.0e-4
    Iz = 1.0e-4
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
  [./density]
    type = GenericConstantMaterial
    block = 0
    prop_names = 'density'
    prop_values = '1.0'
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
  [./vel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = vel_y
  [../]
  [./accel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = accel_y
  [../]
[]

[Outputs]
  exodus = true
  csv = true
  perf_graph = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/dynamic/dyn_euler_small.i)

Results

For this beam, the dimensionless parameter alpha is given by: alpha=kAGL2EI=6.4×106alpha = \frac {kAGL^2}{EI} = 6.4\times 10^6 Therefore, the beam behaves like an Euler-Bernoulli beam. The displacement, velocity and acceleration, as the function of time, at the free end of the cantilever beam in MOOSE, are compared with the results from ABAQUS using the time step of 0.05 s, as shown in Figure 8, Figure 9 and Figure 10.

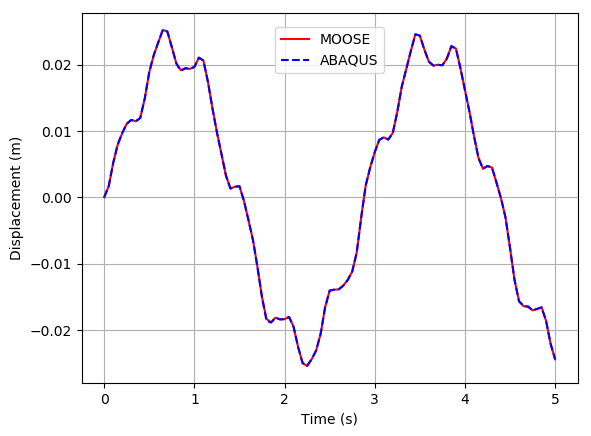
Figure 8: Displacement at the free end of the Euler beam.

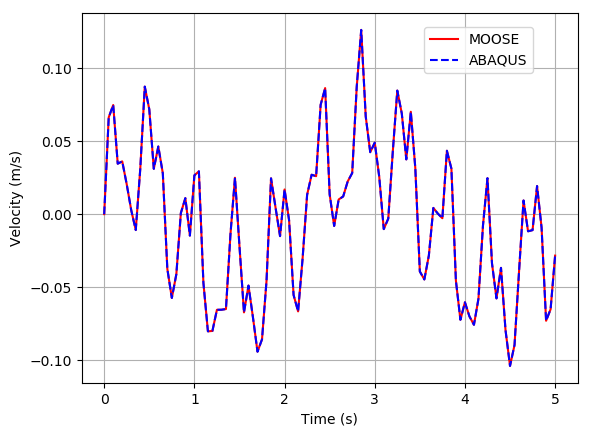
Figure 9: Velocity at the free end of the Euler beam.

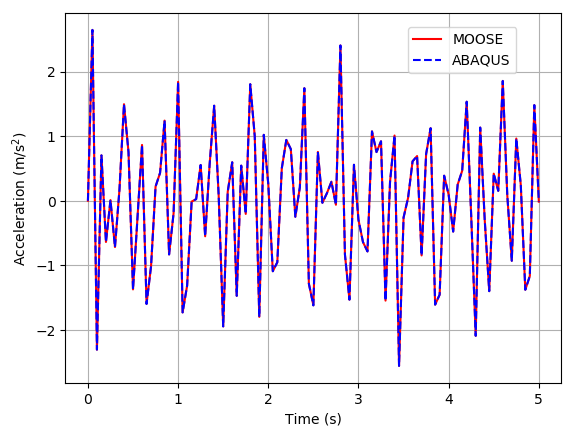
Figure 10: Acceleration at the free end of the Euler beam.

Small strain Timoshenko beam vibration

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam has a cross section area of 1 m2{m}^2, moment of inertia about Y and Z axis of 1 m4{m}^4, Young's modulus of elasticity of 2×\times104^4 N/m2{m}^2, poisson's ratio of -0.99, density of 1 kg/m3{m}^3, shear modulus of 1×\times104^4 N/m2{m}^2 and shear coefficient of 1. An impulse load with a peak value of 0.01 N at 0.0.005 s, as shown in Figure 11, is applied at the free end of the beam in Y direction. The Newmark time integration parameters used in the problem correspond to the Newmark's average acceleration method, i.e., beta=0.25 and gamma=0.5

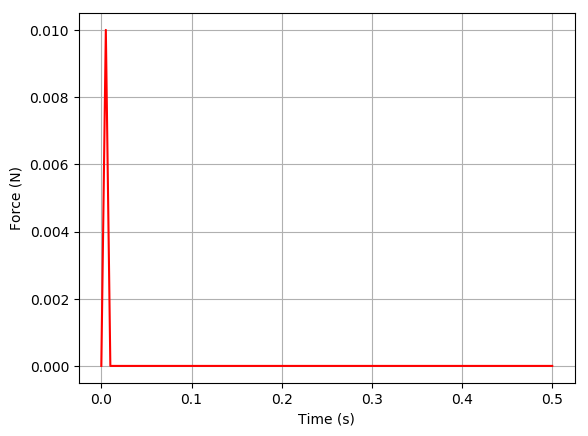
Figure 11: Impulse load pattern applied at the free end of the beam.

# Test for small strain Timoshenko beam vibration in y direction

# An impulse load is applied at the end of a cantilever beam of length 4m.
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 2e4
# Shear modulus (G) = 1e4
# Shear coefficient (k) = 1.0
# Cross-section area (A) = 1.0
# Iy = 1.0 = Iz
# Length (L)= 4 m
# density (rho) = 1.0

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 8
# Therefore, the beam behaves like a Timoshenko beam.

# The FEM solution for this beam with 100 elements give first natural period of 0.2731s with a time step of 0.005.
# The acceleration, velocity and displacement time histories obtained from MOOSE matches with those obtained from ABAQUS.

# Values from the first few time steps are as follows:
# time    disp_y                vel_y                 accel_y
# 0.0     0.0                   0.0                   0.0
# 0.005   2.5473249455812e-05   0.010189299782325     4.0757199129299
# 0.01    5.3012872677486e-05   0.00082654950634483  -7.8208200233219
# 0.015   5.8611622914354e-05   0.0014129505884026    8.055380456145
# 0.02    6.766113649781e-05    0.0022068548449798   -7.7378187535141
# 0.025   7.8981810558437e-05   0.0023214147792709    7.7836427272305

# Note that the theoretical first frequency of the beam using Euler-Bernoulli theory is:
# f1 = 1/(2 pi) * (3.5156/L^2) * sqrt(EI/rho) = 4.9455

# This implies that the corresponding time period of this beam (under Euler-Bernoulli assumption) is 0.2022s.

# This shows that Euler-Bernoulli beam theory under-predicts the time period of a thick beam. In other words, the Euler-Bernoulli beam theory predicts a more compliant beam than reality for a thick beam.

[Mesh]
  type = GeneratedMesh
  xmin = 0
  xmax = 4.0
  nx = 100
  dim = 1
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[AuxVariables]
  [./vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
[]

[AuxKernels]
  [./accel_x]
    type = NewmarkAccelAux
    variable = accel_x
    displacement = disp_x
    velocity = vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_x]
    type = NewmarkVelAux
    variable = vel_x
    acceleration = accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_y]
    type = NewmarkAccelAux
    variable = accel_y
    displacement = disp_y
    velocity = vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_y]
    type = NewmarkVelAux
    variable = vel_y
    acceleration = accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_z]
    type = NewmarkAccelAux
    variable = accel_z
    displacement = disp_z
    velocity = vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_z]
    type = NewmarkVelAux
    variable = vel_z
    acceleration = accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_x]
    type = NewmarkAccelAux
    variable = rot_accel_x
    displacement = rot_x
    velocity = rot_vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_x]
    type = NewmarkVelAux
    variable = rot_vel_x
    acceleration = rot_accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_y]
    type = NewmarkAccelAux
    variable = rot_accel_y
    displacement = rot_y
    velocity = rot_vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_y]
    type = NewmarkVelAux
    variable = rot_vel_y
    acceleration = rot_accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_z]
    type = NewmarkAccelAux
    variable = rot_accel_z
    displacement = rot_z
    velocity = rot_vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_z]
    type = NewmarkVelAux
    variable = rot_vel_z
    acceleration = rot_accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = UserForcingFunctionNodalKernel
    variable = disp_y
    boundary = right
    function = force
  [../]
[]

[Functions]
  [./force]
    type = PiecewiseLinear
    x = '0.0 0.005 0.01 1.0'
    y = '0.0 1.0  0.0  0.0'
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]

[Executioner]
  type = Transient
  solve_type = NEWTON
  line_search = 'none'
  nl_rel_tol = 1e-11
  nl_abs_tol = 1e-11
  start_time = 0.0
  dt = 0.005
  end_time = 0.5
  timestep_tolerance = 1e-6
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
  [./inertial_force_x]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 0
    variable = disp_x
  [../]
  [./inertial_force_y]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 1
    variable = disp_y
  [../]
  [./inertial_force_z]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 2
    variable = disp_z
  [../]
  [./inertial_force_rot_x]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 3
    variable = rot_x
  [../]
  [./inertial_force_rot_y]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 4
    variable = rot_y
  [../]
  [./inertial_force_rot_z]
    type = InertialForceBeam
    block = 0
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    velocities = 'vel_x vel_y vel_z'
    accelerations = 'accel_x accel_y accel_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations = 'rot_accel_x rot_accel_y rot_accel_z'
    beta = 0.25
    gamma = 0.5
    area = 1.0
    Iy = 1.0
    Iz = 1.0
    Ay = 0.0
    Az = 0.0
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 2e4
    poissons_ratio = 0.0
    shear_coefficient = 1.0
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 1.0
    Ay = 0.0
    Az = 0.0
    Iy = 1.0
    Iz = 1.0
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
  [./density]
    type = GenericConstantMaterial
    block = 0
    prop_names = 'density'
    prop_values = '1.0'
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
  [./vel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = vel_y
  [../]
  [./accel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = accel_y
  [../]
[]

[Outputs]
  exodus = true
  csv = true
  perf_graph = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/dynamic/dyn_timoshenko_small.i)

Results

For this beam, the dimensionless parameter alpha is given by: alpha=kAGL2EI=8alpha = \frac {kAGL^2}{EI} = 8 Therefore, the beam behaves like a Timoshenko beam. The displacement, velocity and acceleration, as the function of time, at the free end of the cantilever beam in MOOSE, are compared with the results from ABAQUS using the time step of 0.005 s, as shown in Figure 12, Figure 13 and Figure 14.

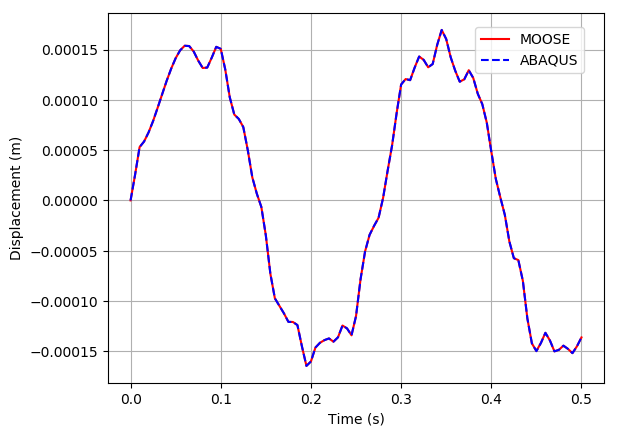
Figure 12: Displacement at the free end of the Timoshenko beam.

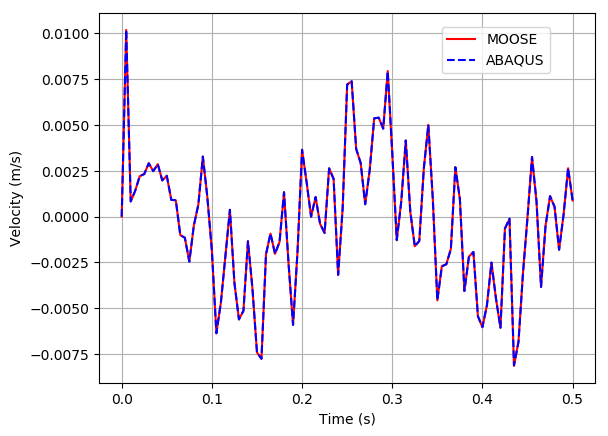
Figure 13: Velocity at the free end of the Timoshenko beam.

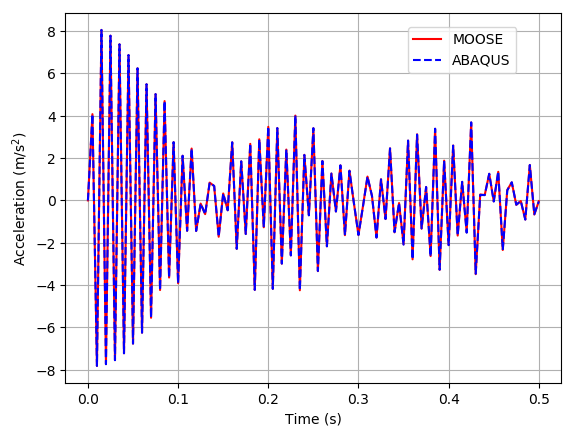
Figure 14: Acceleration at the free end of the Timoshenko beam.

Small strain massless beam vibration with a lumped mass

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam is massless with a lumped mass of 0.0189972 kgs at its free end. The beam has a moment of inertia of 1×\times10−^-4^4 m4{m}^4 about Y and Z axis, Young's modulus of elasticity of 1×\times104^4 N/m2{m}^2, poisson's ratio of -0.99, shear modulus of 4×\times107^7 N/m2{m}^2 and shear coefficient of 1. An impulse load with a peak value of 0.01 N at 0.1 s, as shown in Figure 15, is applied at the free end of the beam in Y direction. The Newmark time integration parameters used in the problem correspond to the Newmark's average acceleration method, i.e., beta=0.25 and gamma=0.5.

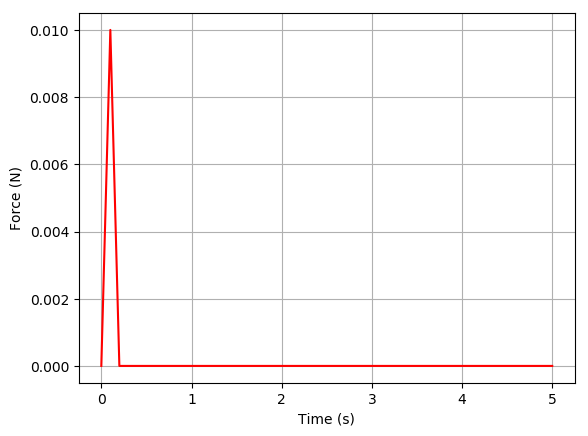
Figure 15: Impulse load pattern applied at the free end of the beam.

# Test for small strain euler beam vibration in y direction

# An impulse load is applied at the end of a cantilever beam of length 4m.
# The beam is massless with a lumped mass at the end of the beam
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 1e4
# Shear modulus (G) = 4e7
# Shear coefficient (k) = 1.0
# Cross-section area (A) = 0.01
# Iy = 1e-4 = Iz
# Length (L)= 4 m
# mass (m) = 0.01899772

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 6.4e6
# Therefore, the beam behaves like a Euler-Bernoulli beam.

# The theoretical first frequency of this beam is:
# f1 = 1/(2 pi) * sqrt(3EI/(mL^3)) = 0.25

# This implies that the corresponding time period of this beam is 4s.

# The FEM solution for this beam with 10 element gives time periods of 4s with time step of 0.01s.
# A higher time step of 0.1 s is used in the test to reduce computational time.

# The time history from this analysis matches with that obtained from Abaqus.

# Values from the first few time steps are as follows:
# time   disp_y                vel_y                accel_y
# 0.0    0.0                   0.0                  0.0
# 0.1    0.0013076435060869    0.026152870121738    0.52305740243477
# 0.2    0.0051984378734383    0.051663017225289   -0.01285446036375
# 0.3    0.010269120909367     0.049750643493289   -0.02539301427625
# 0.4    0.015087433925158     0.046615616822532   -0.037307519138892
# 0.5    0.019534963888307     0.042334982440433   -0.048305168503101

[Mesh]
  type = GeneratedMesh
  xmin = 0.0
  xmax = 4.0
  nx = 10
  dim = 1
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[AuxVariables]
  [./vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
[]

[AuxKernels]
  [./accel_x]
    type = NewmarkAccelAux
    variable = accel_x
    displacement = disp_x
    velocity = vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_x]
    type = NewmarkVelAux
    variable = vel_x
    acceleration = accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_y]
    type = NewmarkAccelAux
    variable = accel_y
    displacement = disp_y
    velocity = vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_y]
    type = NewmarkVelAux
    variable = vel_y
    acceleration = accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_z]
    type = NewmarkAccelAux
    variable = accel_z
    displacement = disp_z
    velocity = vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_z]
    type = NewmarkVelAux
    variable = vel_z
    acceleration = accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = UserForcingFunctionNodalKernel
    variable = disp_y
    boundary = right
    function = force
  [../]
  [./x_inertial]
    type = NodalTranslationalInertia
    variable = disp_x
    velocity = vel_x
    acceleration = accel_x
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
  [../]
  [./y_inertial]
    type = NodalTranslationalInertia
    variable = disp_y
    velocity = vel_y
    acceleration = accel_y
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
  [../]
  [./z_inertial]
    type = NodalTranslationalInertia
    variable = disp_z
    velocity = vel_z
    acceleration = accel_z
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
  [../]
[]

[Functions]
  [./force]
    type = PiecewiseLinear
    x = '0.0 0.1 0.2 10.0'
    y = '0.0 1e-2  0.0  0.0'
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]

[Executioner]
  type = Transient
  solve_type = NEWTON

  petsc_options_iname = '-ksp_type -pc_type'
  petsc_options_value = 'preonly   lu'

  dt = 0.1
  end_time = 5.0
  timestep_tolerance = 1e-6
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 1.0e4
    poissons_ratio = -0.999875
    shear_coefficient = 1.0
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 0.01
    Ay = 0.0
    Az = 0.0
    Iy = 1.0e-4
    Iz = 1.0e-4
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
  [./vel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = vel_y
  [../]
  [./accel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = accel_y
  [../]
[]

[Outputs]
  exodus = true
  csv = true
  perf_graph = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/dynamic/dyn_euler_small_added_mass.i)

Results

The displacement, velocity and acceleration, as the function of time, at the free end of the cantilever beam in MOOSE, are compared with the results from ABAQUS using the time step of 0.1 s, as shown in Figure 16, Figure 17 and Figure 18.

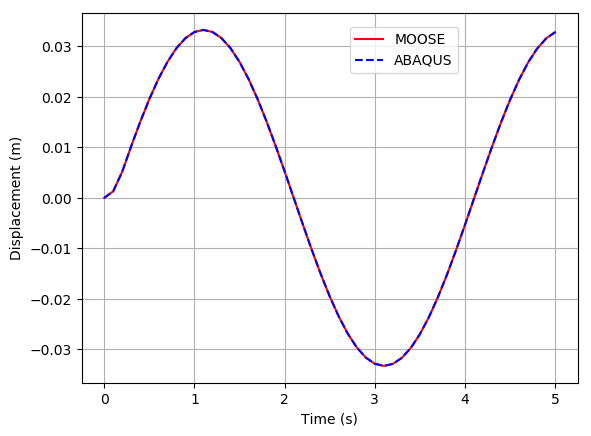
Figure 16: Displacement at the free end of the massless beam with lumped mass.

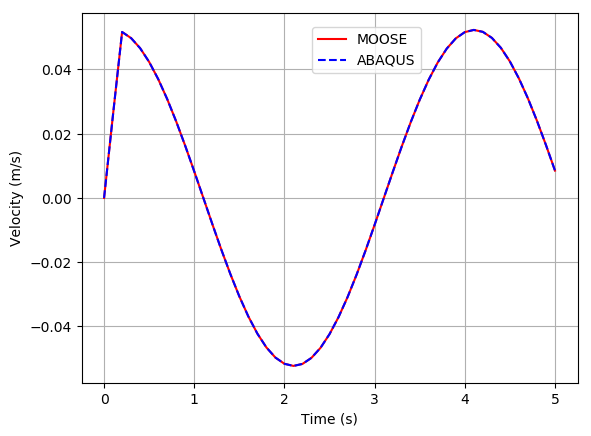
Figure 17: Velocity at the free end of the massless beam with lumped mass.

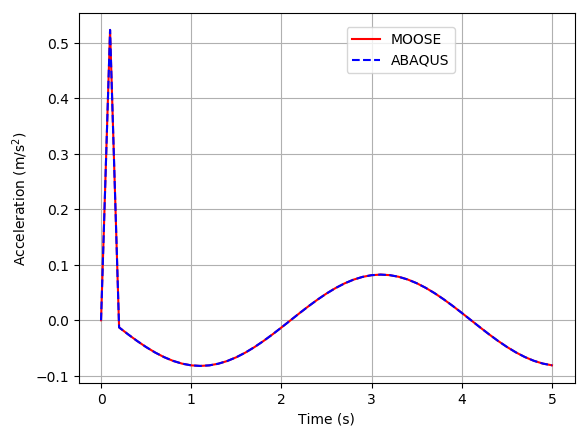
Figure 18: Acceleration at the free end of the massless beam with lumped mass.

Small strain massless beam damped vibration with a lumped mass having rotational moment of inertia

A 1D cantilever beam of 4 m is modeled using beam elements in MOOSE. The beam is massless with a lumped mass of 0.01899772 kgs at its free end whose moment of inertia about X, Y and Z axis is 0.2 m4{m}^4,0.1 m4{m}^4 and 0.1 m4{m}^4, . The beam has a moment of inertia about Y and Z axis of 1×\times10−^-4^4 m4{m}^4, Young's modulus of elasticity of 1×\times104^4 N/m2{m}^2, poisson's ratio of -0.99, shear modulus of 4×\times107^7 N/m2{m}^2 and shear coefficient of 1. An impulse load with a peak value of 0.01 N at 0.1 s as shown in Figure 19 is applied at the free end of the beam in Y direction. The Newmark time integration parameters used in the problem correspond to the Newmark's average acceleration method, i.e., beta=0.25 and gamma=0.5 and vibration is damping using the mass proportional coefficient eta=0.1.

Figure 19: Impulse load pattern applied at the free end of the beam.

# Test for small strain euler beam vibration in y direction

# An impulse load is applied at the end of a cantilever beam of length 4m.
# The beam is massless with a lumped mass at the end of the beam. The lumped
# mass also has a moment of inertia associated with it.
# The properties of the cantilever beam are as follows:
# Young's modulus (E) = 1e4
# Shear modulus (G) = 4e7
# Shear coefficient (k) = 1.0
# Cross-section area (A) = 0.01
# Iy = 1e-4 = Iz
# Length (L)= 4 m
# mass (m) = 0.01899772
# Moment of inertia of lumped mass:
# Ixx = 0.2
# Iyy = 0.1
# Izz = 0.1
# mass proportional damping coefficient (eta) = 0.1

# For this beam, the dimensionless parameter alpha = kAGL^2/EI = 6.4e6
# Therefore, the beam behaves like a Euler-Bernoulli beam.

# The displacement time history from this analysis matches with that obtained from Abaqus.

# Values from the first few time steps are as follows:
# time   disp_y              vel_y               accel_y
# 0.0    0.0                 0.0                 0.0
# 0.1    0.001278249649738   0.025564992994761   0.51129985989521
# 0.2    0.0049813090917644  0.048496195845768  -0.052675802875074
# 0.3    0.0094704658873002  0.041286940064947  -0.091509312741339
# 0.4    0.013082280729802   0.03094935678508   -0.115242352856
# 0.5    0.015588313103503   0.019171290688959  -0.12031896906642

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 10
  xmin = 0.0
  xmax = 4.0
  displacements = 'disp_x disp_y disp_z'
[]

[Variables]
  [./disp_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./disp_z]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_x]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_y]
    order = FIRST
    family = LAGRANGE
  [../]
  [./rot_z]
    order = FIRST
    family = LAGRANGE
  [../]
[]

[AuxVariables]
  [./vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_vel_z]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_x]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_y]
  order = FIRST
  family = LAGRANGE
  [../]
  [./rot_accel_z]
  order = FIRST
  family = LAGRANGE
  [../]
[]

[AuxKernels]
  [./accel_x]
    type = NewmarkAccelAux
    variable = accel_x
    displacement = disp_x
    velocity = vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_x]
    type = NewmarkVelAux
    variable = vel_x
    acceleration = accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_y]
    type = NewmarkAccelAux
    variable = accel_y
    displacement = disp_y
    velocity = vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_y]
    type = NewmarkVelAux
    variable = vel_y
    acceleration = accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./accel_z]
    type = NewmarkAccelAux
    variable = accel_z
    displacement = disp_z
    velocity = vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./vel_z]
    type = NewmarkVelAux
    variable = vel_z
    acceleration = accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_x]
    type = NewmarkAccelAux
    variable = rot_accel_x
    displacement = rot_x
    velocity = rot_vel_x
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_x]
    type = NewmarkVelAux
    variable = rot_vel_x
    acceleration = rot_accel_x
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_y]
    type = NewmarkAccelAux
    variable = rot_accel_y
    displacement = rot_y
    velocity = rot_vel_y
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_y]
    type = NewmarkVelAux
    variable = rot_vel_y
    acceleration = rot_accel_y
    gamma = 0.5
    execute_on = timestep_end
  [../]
  [./rot_accel_z]
    type = NewmarkAccelAux
    variable = rot_accel_z
    displacement = rot_z
    velocity = rot_vel_z
    beta = 0.25
    execute_on = timestep_end
  [../]
  [./rot_vel_z]
    type = NewmarkVelAux
    variable = rot_vel_z
    acceleration = rot_accel_z
    gamma = 0.5
    execute_on = timestep_end
  [../]
[]

[BCs]
  [./fixx1]
    type = DirichletBC
    variable = disp_x
    boundary = left
    value = 0.0
  [../]
  [./fixy1]
    type = DirichletBC
    variable = disp_y
    boundary = left
    value = 0.0
  [../]
  [./fixz1]
    type = DirichletBC
    variable = disp_z
    boundary = left
    value = 0.0
  [../]
  [./fixr1]
    type = DirichletBC
    variable = rot_x
    boundary = left
    value = 0.0
  [../]
  [./fixr2]
    type = DirichletBC
    variable = rot_y
    boundary = left
    value = 0.0
  [../]
  [./fixr3]
    type = DirichletBC
    variable = rot_z
    boundary = left
    value = 0.0
  [../]
[]

[NodalKernels]
  [./force_y2]
    type = UserForcingFunctionNodalKernel
    variable = disp_y
    boundary = right
    function = force
  [../]
  [./x_inertial]
    type = NodalTranslationalInertia
    variable = disp_x
    velocity = vel_x
    acceleration = accel_x
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
    eta = 0.1
  [../]
  [./y_inertial]
    type = NodalTranslationalInertia
    variable = disp_y
    velocity = vel_y
    acceleration = accel_y
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
    eta = 0.1
  [../]
  [./z_inertial]
    type = NodalTranslationalInertia
    variable = disp_z
    velocity = vel_z
    acceleration = accel_z
    boundary = right
    beta = 0.25
    gamma = 0.5
    mass = 0.01899772
    eta = 0.1
  [../]
  [./rot_x_inertial]
    type = NodalRotationalInertia
    variable = rot_x
    rotations = 'rot_x rot_y rot_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations= 'rot_accel_x rot_accel_y rot_accel_z'
    boundary = right
    beta = 0.25
    gamma = 0.5
    Ixx = 2e-1
    Iyy = 1e-1
    Izz = 1e-1
    eta = 0.1
    component = 0
  [../]
  [./rot_y_inertial]
    type = NodalRotationalInertia
    variable = rot_y
    rotations = 'rot_x rot_y rot_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations= 'rot_accel_x rot_accel_y rot_accel_z'
    boundary = right
    beta = 0.25
    gamma = 0.5
    Ixx = 2e-1
    Iyy = 1e-1
    Izz = 1e-1
    eta = 0.1
    component = 1
  [../]
  [./rot_z_inertial]
    type = NodalRotationalInertia
    variable = rot_z
    rotations = 'rot_x rot_y rot_z'
    rotational_velocities = 'rot_vel_x rot_vel_y rot_vel_z'
    rotational_accelerations= 'rot_accel_x rot_accel_y rot_accel_z'
    boundary = right
    beta = 0.25
    gamma = 0.5
    Ixx = 2e-1
    Iyy = 1e-1
    Izz = 1e-1
    eta = 0.1
    component = 2
  [../]
[]

[Functions]
  [./force]
    type = PiecewiseLinear
    x = '0.0 0.1 0.2 10.0'
    y = '0.0 1e-2  0.0  0.0'
  [../]
[]

[Preconditioning]
  [./smp]
    type = SMP
    full = true
  [../]
[]

[Executioner]
  type = Transient
  solve_type = NEWTON

  petsc_options_iname = '-ksp_type -pc_type'
  petsc_options_value = 'preonly   lu'

  dt = 0.1
  end_time = 5.0
  timestep_tolerance = 1e-6
[]

[Kernels]
  [./solid_disp_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 0
    variable = disp_x
  [../]
  [./solid_disp_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 1
    variable = disp_y
  [../]
  [./solid_disp_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 2
    variable = disp_z
  [../]
  [./solid_rot_x]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 3
    variable = rot_x
  [../]
  [./solid_rot_y]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 4
    variable = rot_y
  [../]
  [./solid_rot_z]
    type = StressDivergenceBeam
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    component = 5
    variable = rot_z
  [../]
[]

[Materials]
  [./elasticity]
    type = ComputeElasticityBeam
    youngs_modulus = 1.0e4
    poissons_ratio = -0.999875
    shear_coefficient = 1.0
    block = 0
  [../]
  [./strain]
    type = ComputeIncrementalBeamStrain
    block = '0'
    displacements = 'disp_x disp_y disp_z'
    rotations = 'rot_x rot_y rot_z'
    area = 0.01
    Ay = 0.0
    Az = 0.0
    Iy = 1.0e-4
    Iz = 1.0e-4
    y_orientation = '0.0 1.0 0.0'
  [../]
  [./stress]
    type = ComputeBeamResultants
    block = 0
  [../]
[]

[Postprocessors]
  [./disp_x]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_x
  [../]
  [./disp_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = disp_y
  [../]
  [./vel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = vel_y
  [../]
  [./accel_y]
    type = PointValue
    point = '4.0 0.0 0.0'
    variable = accel_y
  [../]
[]

[Outputs]
  exodus = true
  csv = true
  perf_graph = true
[]
(contrib/moose/modules/solid_mechanics/test/tests/beam/dynamic/dyn_euler_small_added_mass_inertia_damping.i)

Results

The displacement, velocity and acceleration, as the function of time, at the free end of the cantilever beam in MOOSE, are compared with the results from ABAQUS using the time step of 0.1 s, as shown in Figure 20, Figure 21 and Figure 22.

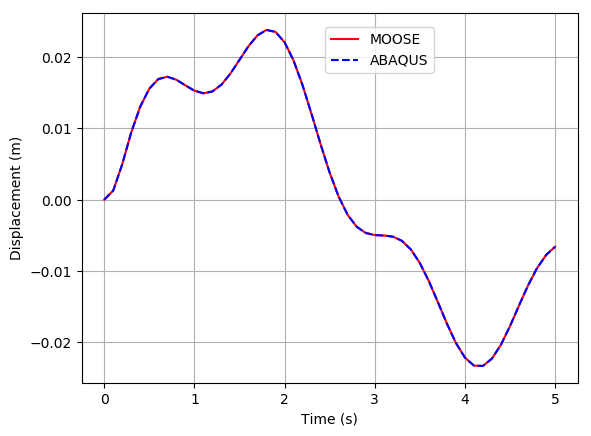
Figure 20: Displacement at the free end of the massless beam with lumped mass having rotational moment of inertia.

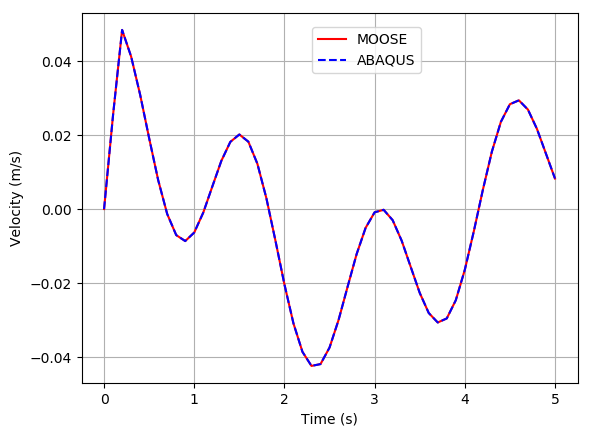
Figure 21: Velocity at the free end of the massless beam with lumped mass having rotational moment of inertia.

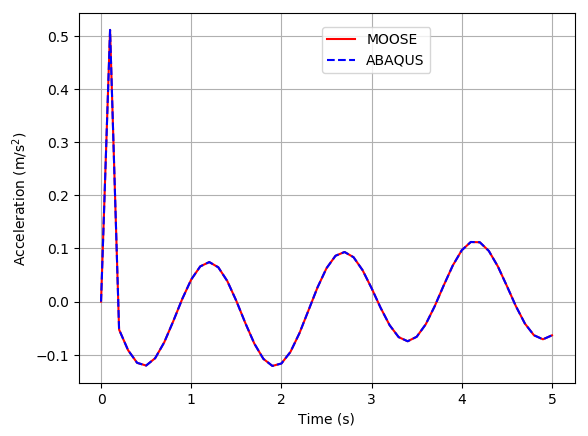
Figure 22: Acceleration at the free end of the massless beam with lumped mass having rotational moment of inertia.

References

  1. K. E. BISSHOPP and D. C. DRUCKER. Large deflection of cantilever beams. Quarterly of Applied Mathematics, 3(3):272–275, 1945. URL: http://www.jstor.org/stable/43633516.[BibTeX]