The NekRS solution in element , or , is a linear combination of polynomials and coefficients ,

(1)

where is the polynomial order. In NekRS, the polynomials are Lagrange interpolants of Gauss-Lobatto-Legendre (GLL) quadrature points, for such that . To help explain the interpolation between NekRS's high-order solution and the lower-order mesh mirror, Figure 1 shows a 1-D element with a third-order NekRS solution (the black curved line) based on four GLL points (blue dots).

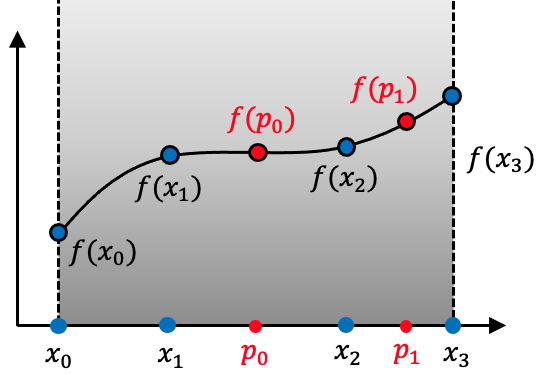
Figure 1: Interpolation between a high-order NekRS solution (based on GLL quadrature points ) and generic points

To interpolate this solution to a MOOSE element with arbitrary nodes (red dots),

(2)

The first matrix on the right-hand side of Eq. (2) is referred to as a Vandermonde matrix. The interpolation is performed by evaluating the NekRS solution using the polynomial solution in Eq. (1) at the MOOSE nodes using Vandermonde matrices.

This formulation is then extended to the problem-specific polynomial order, where the NekRS quadrature points are determined based on the poynomial order (since NekRS always uses the GLL quadrature) and the MOOSE quadrature points are determined based on the combination of the order of the variables temp, avg_flux, and heat_source plus the quadrature rule specified in the input file.